浙江省宁波市余姚市2022-2023学年九年级上学期期末考试数学试卷

试卷更新日期：2023-02-23 类型：期末考试

进入出卷网下载

一、选择题(每小题4分，共40分.)

1. 抛物线y=2(x-3)²+7的对称轴为（）

A、直线x=3 B、直线x=-3 C、直线x=2 D、直线x=7

查看试题解析
2. 下列事件中，属于必然事件的是（）

A、射击运动员射击一次，命中10 环 B、有一匹马奔跑的速度是70米/秒 C、任意抛掷一只纸杯，杯口朝下 D、在地面上向空中抛掷一石块，石块终将落下

查看试题解析
3. 已知线段a=3，b=12，则a，b的比例中项线段等于（）

A、2 B、4 C、6 D、9

查看试题解析
4. 已知圆的半径为5cm，同一平面内一点到圆心的距离是6cm，则这点在（）

A、圆外 B、圆上 C、圆内 D、不能确定

查看试题解析
5. 在Rt△ABC中，∠C=90°，AC=4，AB=5，则cosA的值为（）

A、 $\frac{3}{4}$ B、 $\frac{3}{5}$ C、 $\frac{4}{5}$ D、 $\frac{5}{4}$

查看试题解析
6. 如图，在△ABC中，DE∥BC，若 $\frac{A D}{D B} = \frac{1}{2}$ ，则△ADE与△ABC的面积之比为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{9}$

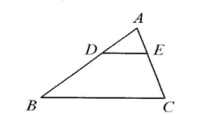查看试题解析
7. 如图，正六边形ABCDEF内接于⊙O，点M在 $\overset{⌢}{A B}$ 上，则∠CME的度数为（）

A、36° B、45° C、60° D、75°

查看试题解析
8. 如图，已知直线l₁∥l₂∥l₃ ，直线AB分别交三条平行线于点A、E、B，直线CD分别交三条平行线于点C、F、D，直线AB、CD相交于点O，若AE：EO：OB=4：2：7，则下列式子① $\frac{O F}{O C} = \frac{1}{3}$ ；② $\frac{C F}{F D} = \frac{4}{9}$ ；③ $\frac{E F}{D B} = \frac{2}{7}$ ；④ $\frac{E F}{A C} = \frac{1}{2}$ 中，正确的个数有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
9. 如图，在△ABC中，AB<AC，将△ABC以点A为旋转中心逆时针旋转得到△ADE，点D在BC边上，DE交AC于点F，则下列结论中错误的是（）

A、△AFE∽△DFC B、AD=AF C、DA平分∠BDE D、∠CDF=∠BAD

查看试题解析
10. 如图，抛物线y=x²+bx+c (b， c为常数)经过点A (1，0)，点B (0，3)，点P在该抛物线上，其横坐标为m，若该抛物线在点P左侧部分(包括点P)的最低点的纵坐标为2-m．则m的值为（）

A、m=3 B、m= $\frac{3 - \sqrt{5}}{2}$ C、m= $\frac{3 \pm \sqrt{5}}{2}$ D、m=3或m= $\frac{3 - \sqrt{5}}{2}$

查看试题解析

二、填空题(每小题5分，共30分)

11. 若两个相似多边形的相似比是2：3，则它们的周长比是 .

查看试题解析

12. “头盔是生命之盔”，质检部门]对某工厂生产的头盔质量进行抽查，抽查结果如下表：

抽查的头盔数n	100	200	300	500	800	1000
合格的头盔数m	95	194	289	479	769	960
合格头盔的频率 $\frac{m}{n}$	0.950	0.945	0.962	0.958	0.961	0.960

请估计该工厂生产10000个头盔，合格的头盔数约有个．

查看试题解析

13. 若一个扇形的半径为3，圆心角为120°，则此扇形的弧长为.

查看试题解析
14. 如图，在△ABC中，∠AED=∠B，若AB=10，AE=8，DE=6，则BC的长为.

查看试题解析
15. 如图，抛物线y=ax²-2ax+3 (a>0)与y轴交于点A，过点A作x轴的平行线交抛物线于点M，P为抛物线的顶点，若直线OP交直线AM于点B，且M为线段AB的中点，则线段PB的长为.

查看试题解析
16. 定义：有一个圆分别和一个三角形的三条边各有两个交点，截得的三条弦相等，我们把这个圆叫作“等弦圆”，现在有一个斜边长为6的等腰直角三角形，当等弦圆最大时，这个圆的半径为 .

查看试题解析

三、解答题{第17、18、19题各8分，第20、21、22题各10分，第23题12分，第24题14分，共80分)

17. 计算：

(1)、cos45°+3tan30°-2sin 60°

(2)、已知 $\frac{x}{y} = \frac{1}{2}$ ，求 $\frac{2 x + 3 y}{y}$ 的值．

查看试题解析
18. 小明和小刚用如图的两个转盘做游戏，游戏规则如下：分别转动两个转盘，当两个转盘指针指向的数字之积为奇数时，小明获胜：数字之积为偶数时，小刚获胜． (若指针恰好指在等分线上时重新转动转盘)

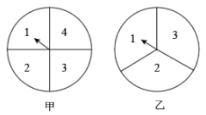(1)、用画树状图或列表的方法求出小明和小刚获胜的概率．

(2)、这个游戏规则是否公平？说明理由．

查看试题解析
19. 如图，在6×6的正方形网格中，点A，B，C均在格点上，请按要求画图．

(1)、在图1中，将△CAB绕C点逆时针旋转90°，作出经旋转后的图形△CA'B'．(其中A'，B'分别是A，B的对应点)

(2)、在图2中画一个格点△ADE，使得△ADE∽△ABC。(画出一个即可)

查看试题解析
20. 消防车是救援火灾的主要装备．图①是一辆登高云梯消防车的实物图，图②是其工作示意图，起重臂AC(20米≤AC≤30米)是可伸缩的，且起重臂AC可绕点A在一定范围内上下转动，张角∠CAE (90°≤∠CAE≤150°)，转动点A距离地面的高度AE为3米．

(1)、当起重臂AC的长为24米，张角∠CAE=120°时，求云梯消防车最高点C距离地面的高度CF．

(2)、某日一栋大楼突发火灾，着火点距离地面的高度为26米，问该消防车在这栋楼下能否实施有效救援？请说明理由． (参考数据： $\sqrt{3}$ ≈1.7) ( 提示：当起重臂AC伸到最长且张角∠CAE最大时，云梯顶端C可以达到最大高度．)

查看试题解析
21. 如图，在△ABC中，以AB为直径的⊙O分别交BC，AC于点D，E．

(1)、求证：△ABC∽△DEC．

(2)、若点D为 $\overset{⌢}{B E}$ 的中点，CD= $\sqrt{3}$ ， AB=4，求CE的长．

查看试题解析
22. 如图，足球运动员在O点处将球射向球门，球射门的路线呈抛物线．当球飞行的水平距离为6米时，球达到最高点，此时球离地面3米．

(1)、求球运动路线的函数表达式．

(2)、若球门在O点正前方10米，球门高度是2.44米，问该球能否射入球门？

查看试题解析
23. 如图

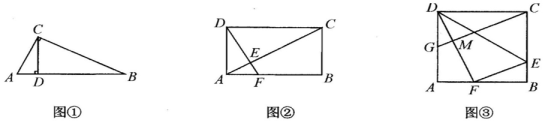(1)、[基础巩固]如图①，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，求证：AC²=AD·AB．

(2)、[尝试应用] 如图②，在矩形ABCD中，AD=2，点F在AB上，FB=2AF，DF⊥AC于点E，求AE的长．

(3)、[拓展提高] 如图③，在矩形ABCD中，点E在边BC上，NDCE与NDFE关于直线DE对称，点C的对称点F在边AB上，G为AD中点，连结GC交DF于点M，GC∥FE，若AD=2，求GM的长．

查看试题解析
24. 如图，△ABC内接于⊙O，过点O作OH⊥BC于点H，延长OH交⊙O于点D，连接AD、BD，AD与BC交于点E，AD=9．

(1)、求证：∠BAD=∠CAD．

(2)、若OH=DH．
①求∠BAC的度数．

②若⊙O的半径为6，求DE的长．

(3)、设BD=x，AB·CE=y，求y关于x的函数表达式．

查看试题解析