四川省成都市武侯区2021-2022学年七年级下学期第一次月考数学试题
试卷更新日期:2023-02-23 类型:月考试卷
一、单选题
-
1. 下面四个图形中,∠1 与∠2是对顶角的图形是( )A、
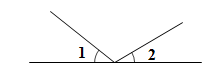 B、
B、 C、
C、 D、
D、 2. 在下列四个图案中,能用平移变换来分析其形成过程的图案是 ( )A、
2. 在下列四个图案中,能用平移变换来分析其形成过程的图案是 ( )A、 B、
B、 C、
C、 D、
D、 3. 下列命题的逆命题是真命题的是( )A、同位角相等 B、对顶角相等 C、钝角三角形有两个锐角 D、两直线平行,内错角相等4.
3. 下列命题的逆命题是真命题的是( )A、同位角相等 B、对顶角相等 C、钝角三角形有两个锐角 D、两直线平行,内错角相等4.如图,点O在直线AB上且OC⊥OD.若∠COA=36°,则∠DOB的大小为( )
 A、36° B、54° C、64° D、72°5.
A、36° B、54° C、64° D、72°5.如图所示,下列说法错误的是( )
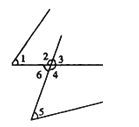 A、∠1和∠3是同位角 B、∠1和∠5是同位角 C、∠1和∠2是同旁内角 D、∠5和∠6是内错角6. 如图,由已知条件推出的结论,正确的是( )
A、∠1和∠3是同位角 B、∠1和∠5是同位角 C、∠1和∠2是同旁内角 D、∠5和∠6是内错角6. 如图,由已知条件推出的结论,正确的是( ) A、由∠1=∠5,可以推出AD∥CB B、由∠4=∠8,可以推出AD∥BC C、由∠2=∠6,可以推出AD∥BC D、由∠3=∠7,可以推出AB∥DC7. 下面计算正确的是( )A、 B、 C、 D、8. 如图, 沿 所在直线向右平移得到 ,已知 ,则平移的距离为( )
A、由∠1=∠5,可以推出AD∥CB B、由∠4=∠8,可以推出AD∥BC C、由∠2=∠6,可以推出AD∥BC D、由∠3=∠7,可以推出AB∥DC7. 下面计算正确的是( )A、 B、 C、 D、8. 如图, 沿 所在直线向右平移得到 ,已知 ,则平移的距离为( )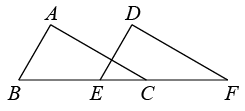 A、5 B、4 C、3 D、69. 下列运算正确的是( )A、 =±3 B、|﹣3|=﹣3 C、 =﹣3 D、 =π﹣4
A、5 B、4 C、3 D、69. 下列运算正确的是( )A、 =±3 B、|﹣3|=﹣3 C、 =﹣3 D、 =π﹣4二、填空题
-
10. 如图,把一块三角板的角的顶点放在直尺的一边上,若 , 则.
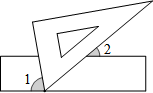 11. 的平方根是 .12. 已知某数的一个平方根是 ,那么它的另一个平方根是.13. 如图,从点P向直线l所画的4条线段中,线段短.
11. 的平方根是 .12. 已知某数的一个平方根是 ,那么它的另一个平方根是.13. 如图,从点P向直线l所画的4条线段中,线段短.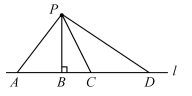 14. 已知: , , 且 , 则a-b的值为.15. 如图,l∥m,∠1=115°,∠2=95°,则∠3=.
14. 已知: , , 且 , 则a-b的值为.15. 如图,l∥m,∠1=115°,∠2=95°,则∠3=.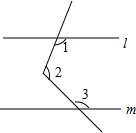 16. 如图,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′E交AF于点G,若∠CEF=70°,则∠GFD′=°.
16. 如图,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′E交AF于点G,若∠CEF=70°,则∠GFD′=°.
三、解答题
-
17. 求下列各式中的x的值:(1)、;(2)、;(3)、;(4)、.18. 已知 的立方根是3, 的算术平方根是4,c是 的整数部分.(1)、求a,b,c的值;(2)、求 的平方根.19. 如图,已知AB⊥AD,CD⊥AD,∠1=∠2,求证:DF∥AE.
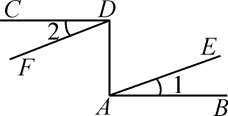 20. 如图,已知∠A=∠FEC,∠DEF=∠B.
20. 如图,已知∠A=∠FEC,∠DEF=∠B. (1)、试判断DE与BC的位置关系,并说明理由.(2)、若DE平分∠ADC,∠BDC=3∠B,求∠EFC的度数.21. 如图,在方格纸内将经过一次平移后得到 , 图中标出了点B的对应点.
(1)、试判断DE与BC的位置关系,并说明理由.(2)、若DE平分∠ADC,∠BDC=3∠B,求∠EFC的度数.21. 如图,在方格纸内将经过一次平移后得到 , 图中标出了点B的对应点. (1)、补全根据下列条件,利用网格点和三角板画图:(2)、画出AB边上的中线CD;(3)、画出BC边上的高线AE;(4)、的面积为.22. 已知AB∥CD,直线MN分别交AB,CD于E、F,∠MFD=50°,EG平分∠MEB,求证:∠MEG的度数为25°.
(1)、补全根据下列条件,利用网格点和三角板画图:(2)、画出AB边上的中线CD;(3)、画出BC边上的高线AE;(4)、的面积为.22. 已知AB∥CD,直线MN分别交AB,CD于E、F,∠MFD=50°,EG平分∠MEB,求证:∠MEG的度数为25°.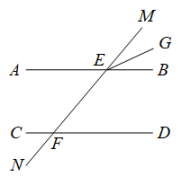 23. 如图,CD是△ABC的高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DGBC.
23. 如图,CD是△ABC的高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DGBC.试判断∠1、∠2的数量关系,并说明理由.
 24. 已知:如图,AB∥CD,∠1=∠2,∠3=∠4.
24. 已知:如图,AB∥CD,∠1=∠2,∠3=∠4.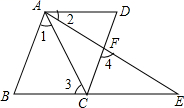 (1)、求证:AD∥BE;(2)、若∠B=∠3=2∠2,求∠D的度数.25. 观察下列等式,根据你发现的规律解决问题:
(1)、求证:AD∥BE;(2)、若∠B=∠3=2∠2,求∠D的度数.25. 观察下列等式,根据你发现的规律解决问题:①;
②;
③;
……
(1)、化简:.(2)、化简:(n为正整数).(3)、利用上面所揭示的规律计算:26. 如图,AB//CD,点E、F分别在直线AB、CD上,点O在直线AB、CD之间,∠EOF=100°.

 (1)、求∠BEO+∠DFO的值;(2)、如图2,直线MN交∠BEO、∠CFO的角平分线分别于点M、N,求∠EMN-∠FNM的值;(3)、如图3,EG在∠AEO内,∠AEG=n∠OEG,FK在∠DFO内,∠DFK =n∠OFK,直线MN交FK、EG分别于点M、N,若∠FMN-∠ENM=50°,则n的值是
(1)、求∠BEO+∠DFO的值;(2)、如图2,直线MN交∠BEO、∠CFO的角平分线分别于点M、N,求∠EMN-∠FNM的值;(3)、如图3,EG在∠AEO内,∠AEG=n∠OEG,FK在∠DFO内,∠DFK =n∠OFK,直线MN交FK、EG分别于点M、N,若∠FMN-∠ENM=50°,则n的值是