四川省成都市天府师大一中麓山校区2021-2022学年七年级下学期3月月考数学试题
试卷更新日期:2023-02-23 类型:月考试卷
一、单选题
-
1. 计算:( )A、 B、 C、 D、2. 下列各式计算正确的是( )A、 B、 C、 D、3. 每到傍晚祥和广场都会有很多小朋友拿着泡泡机吹泡泡玩,其泡泡的厚度大约为0.000326毫米,这个数字用科学记数法表示为( )A、 毫米 B、 毫米 C、 毫米 D、 毫米4. 下列各式能用平方差公式计算的是( )A、 B、 C、 D、5. 若 , 那么满足的条件是( )A、为任意数 B、 C、 D、6. 如图,点在直线上,已知 , , 则的度数为( )
 A、20° B、70° C、110° D、90°7. 如果多项式 是一个完全平方式,则m的值是 ( )A、±4 B、4 C、8 D、± 88. 下列说法:①平面内,过一点有且只有一条直线与已知直线垂直;②相等的角是对顶角;③两条直线被第三条直线所截,同位角相等;④过一点有且只有一条直线与已知直线平行,其中正确的说法有( )A、个 B、个 C、个 D、个9. 如图,点在的延长线上,在下列四个条件中,不能判断的是( )
A、20° B、70° C、110° D、90°7. 如果多项式 是一个完全平方式,则m的值是 ( )A、±4 B、4 C、8 D、± 88. 下列说法:①平面内,过一点有且只有一条直线与已知直线垂直;②相等的角是对顶角;③两条直线被第三条直线所截,同位角相等;④过一点有且只有一条直线与已知直线平行,其中正确的说法有( )A、个 B、个 C、个 D、个9. 如图,点在的延长线上,在下列四个条件中,不能判断的是( ) A、 B、 C、 D、10. 用4个长为 , 宽为的长方形拼成如图所示的大正方形,则用这个图形可以验证的恒等式是( )
A、 B、 C、 D、10. 用4个长为 , 宽为的长方形拼成如图所示的大正方形,则用这个图形可以验证的恒等式是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图, , 点E、F在上,且.则点C到的距离是.
 12. 已知一个角的补角是 , 则这个角是 度.13. 已知 , , 则的值为.14. 如图,直线、相交于点 , 射线平分 , , 若 , 则的度数为.
12. 已知一个角的补角是 , 则这个角是 度.13. 已知 , , 则的值为.14. 如图,直线、相交于点 , 射线平分 , , 若 , 则的度数为.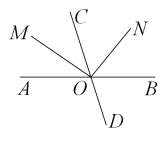 15. 若 , 且 , 则 .16. 已知 , 是多项式,在计算时,小马虎同学把看成了 , 结果得 , 细心的小明同学计算正确,那么小明计算出的值为.17. 已知和的两边互相垂直,且比的两倍少 , 则的度数为 .18. 有一副直角三角板和 , 其中 , , 如图所示叠放,边与边交于点 , 过点作平分 , 若 , 则度.
15. 若 , 且 , 则 .16. 已知 , 是多项式,在计算时,小马虎同学把看成了 , 结果得 , 细心的小明同学计算正确,那么小明计算出的值为.17. 已知和的两边互相垂直,且比的两倍少 , 则的度数为 .18. 有一副直角三角板和 , 其中 , , 如图所示叠放,边与边交于点 , 过点作平分 , 若 , 则度. 19. 在长方形中, , 在线段上任取一点不和点、重叠 , 连接 , 过点作交的延长线于点 , 的角平分线和的角平分线交于点 , 则度.
19. 在长方形中, , 在线段上任取一点不和点、重叠 , 连接 , 过点作交的延长线于点 , 的角平分线和的角平分线交于点 , 则度.
三、解答题
-
20. 计算下列各题(1)、;(2)、;(3)、;(4)、.21. 先化简再求值: , 其中 , 满足.22. 如图, , , , 求的度数,请将解题过程填写完整.

解:∵(已知),
∴ ▲ ( ),
又∵(已知),
∴( ),
∴( )
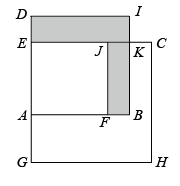
∴+ ▲ ( ),
∵(已知),
∴.
23. 成都东安湖公园内有一块长为米,宽为米的长方形地块,如图所示.成都市规划部门计划将阴影部分绿化,中间将修建一座雕像. (1)、试用含 , 的式子表示绿化部分的面积是多少平方米?(2)、若恒成立,求绿化部分面积.24. 如图,∠1=∠BCE,∠2+∠3=180°.
(1)、试用含 , 的式子表示绿化部分的面积是多少平方米?(2)、若恒成立,求绿化部分面积.24. 如图,∠1=∠BCE,∠2+∠3=180°. (1)、判断AC与EF的位置关系,并说明理由;(2)、若CA平分∠BCE,EF⊥AB于点F,∠1=72°,求∠BAD的度数.25. 如图,已知.
(1)、判断AC与EF的位置关系,并说明理由;(2)、若CA平分∠BCE,EF⊥AB于点F,∠1=72°,求∠BAD的度数.25. 如图,已知. (1)、求证:;(2)、若平分 , 交于点 , 交于点 , 且 , 求的度数.26. 若多项式与的乘积中不含项.(1)、求的值;(2)、已知 , 求的值.
(1)、求证:;(2)、若平分 , 交于点 , 交于点 , 且 , 求的度数.26. 若多项式与的乘积中不含项.(1)、求的值;(2)、已知 , 求的值.