浙江省宁波市镇海区蛟川书院2022-2023学年八年级上学期末数学期末试卷
试卷更新日期:2023-02-23 类型:期末考试
一、单选题
-
1. 下列图形中,不能表示是函数的是( )A、
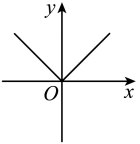 B、
B、 C、
C、 D、
D、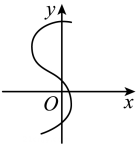 2. 下列运算正确的是( )A、 B、 C、 D、3. 已知 , 则下列不等式一定成立的是( )A、 B、 C、 D、4. 关于x的一元二次方程有两个不相等的实数根,则k的取值范围为( )A、 B、 C、 D、5. 在同一平面直角坐标系中,一次函数()与()的大致图象可以是( )A、
2. 下列运算正确的是( )A、 B、 C、 D、3. 已知 , 则下列不等式一定成立的是( )A、 B、 C、 D、4. 关于x的一元二次方程有两个不相等的实数根,则k的取值范围为( )A、 B、 C、 D、5. 在同一平面直角坐标系中,一次函数()与()的大致图象可以是( )A、 B、
B、 C、
C、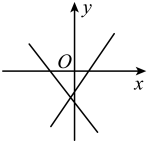 D、
D、 6. 如图是测量一颗玻璃球体积的过程:
6. 如图是测量一颗玻璃球体积的过程:
(1)将的水倒进一个容量为的杯子中;
(2)将五颗相同的玻璃球放入水中,结果水没有满;
(3)再加一颗同样的玻璃球放入水中,结果水满溢出.根据以上过程,推测这样一颗玻璃球的体积范围是( )
A、以上,以下 B、以上,以下 C、以上,以下 D、以上,以下7. 如图,在平面直角坐标系中,已知点 , 点A在第一象限内, , , 将绕点О逆时针旋转,每次旋转90°,则第2023次旋转结束时,点A的坐标为( ) A、 B、 C、 D、8. 对于一元二次方程 , 满足 , 且有两个相等的实数根,则( )A、 B、 C、 D、9. 如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD= AE2;④S△ABC=4S△ADF . 其中正确的有( )
A、 B、 C、 D、8. 对于一元二次方程 , 满足 , 且有两个相等的实数根,则( )A、 B、 C、 D、9. 如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD= AE2;④S△ABC=4S△ADF . 其中正确的有( ) A、1个 B、2 个 C、3 个 D、4个10. 如图,分别以直角三角形的三边向外作等边三角形,然后将较小的两个等边和放在最大的等边内(如图),与交于点P,连结 , .欲求的面积,只需要知道下列哪个三角形的面积即可( )
A、1个 B、2 个 C、3 个 D、4个10. 如图,分别以直角三角形的三边向外作等边三角形,然后将较小的两个等边和放在最大的等边内(如图),与交于点P,连结 , .欲求的面积,只需要知道下列哪个三角形的面积即可( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 使二次根式有意义的x的取值范围是.12. 已知 , 是直线上的两个点,则.(填“”“”或“”)13. 如果一元一次不等式组的解集为 . 则a的取值范围是 .14. 如图,在中, , 于D,平分 , , 则度.
 15. 如图,在Rt△ABC中,∠ABC=90°,AB=6,D为AC中点,过点A作AE∥BC,连结BE,∠EBD=∠CBD,BD=5,则BE的长为.
15. 如图,在Rt△ABC中,∠ABC=90°,AB=6,D为AC中点,过点A作AE∥BC,连结BE,∠EBD=∠CBD,BD=5,则BE的长为.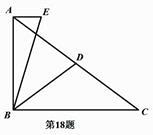 16. 如图,中, , , A是的中点,连结 , 以为直角边做等腰 , 其中.①的长为 , ②连结 , 则的长为.
16. 如图,中, , , A是的中点,连结 , 以为直角边做等腰 , 其中.①的长为 , ②连结 , 则的长为.
三、解答题
-
17. 计算:(1)、;(2)、.18. 解不等式组 , 并把解集表示在数轴上.
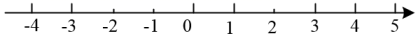 19. 如图,在中, , 过点C作 , , 连接并延长交于点F.
19. 如图,在中, , 过点C作 , , 连接并延长交于点F. (1)、求的度数;(2)、证明:;20. 公安交警部门提醒市民,骑车出行必须严格遵守“一盔一带”的规定.某头盔经销商统计了某品牌头盔4月份到6月份的销量,该品牌头盔4月份销售150个,6月份销售216个,且从4月份到6月份销售量的月增长率相同.(1)、求该品牌头盔销售量的月增长率;(2)、若此种头盔的进价为30元/个,测算在市场中,当售价为40元/个时,月销售量为600个,若在此基础上售价每上涨1元/个,则月销售量将减少10个,为使月销售利润达到10000元,而且尽可能让顾客得到实惠,则该品牌头盔的实际售价应定为多少元/个?21. 如图,在平面直角坐标系中,直线l的解析式为 , 它与坐标轴分别交于A、B两点,已知点B的纵坐标为4.
(1)、求的度数;(2)、证明:;20. 公安交警部门提醒市民,骑车出行必须严格遵守“一盔一带”的规定.某头盔经销商统计了某品牌头盔4月份到6月份的销量,该品牌头盔4月份销售150个,6月份销售216个,且从4月份到6月份销售量的月增长率相同.(1)、求该品牌头盔销售量的月增长率;(2)、若此种头盔的进价为30元/个,测算在市场中,当售价为40元/个时,月销售量为600个,若在此基础上售价每上涨1元/个,则月销售量将减少10个,为使月销售利润达到10000元,而且尽可能让顾客得到实惠,则该品牌头盔的实际售价应定为多少元/个?21. 如图,在平面直角坐标系中,直线l的解析式为 , 它与坐标轴分别交于A、B两点,已知点B的纵坐标为4. (1)、求出A点的坐标.(2)、在第一象限的角平分线上是否存在点Q使得?若存在,求点Q的坐标;若不存在,请说明理由.(3)、点P为y轴上一点,连结AP,若 , 求点P的坐标.22. 如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED边长,易知AE=c,这时我们把关于x的形如的一元二次方程称为“勾系一元二次方程”.
(1)、求出A点的坐标.(2)、在第一象限的角平分线上是否存在点Q使得?若存在,求点Q的坐标;若不存在,请说明理由.(3)、点P为y轴上一点,连结AP,若 , 求点P的坐标.22. 如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED边长,易知AE=c,这时我们把关于x的形如的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)、判断下列方程是否是“勾系一元二次方程”:①(填“是”或“不是”);
②(填“是”或“不是”)
(2)、求证:关于x的“勾系一元二次方程”必有实数根;(3)、若是“勾系一元二次方程”的一个根,且四边形ACDE的周长是12,求△ABC面积.23. (1)、【问题情境】如图1,在中, , 点P为边上的任一点,过点P作 , , 垂足分别为D、E,过点作 , 垂足为F.求证:.(2)、【结论运用】如图 , 将矩形沿折叠,使点D落在点B上,点C落在点处,点P为折痕上的任一点,过点P作、 , 垂足分别为G、H,若 , , 求的值;(3)、【迁移拓展】如图 , 在四边形中, , 为边上的一点, , , 垂足分别为D、C, , , , M、N分别为、的中点,连接、 , 求与的周长之和.24. 如图,在边长为的正方形中,过中点E作正 , 过点F的直线分别交边、于点G、H、已知点M、N分别是线段、的动点,且是等边三角形.
(1)、【问题情境】如图1,在中, , 点P为边上的任一点,过点P作 , , 垂足分别为D、E,过点作 , 垂足为F.求证:.(2)、【结论运用】如图 , 将矩形沿折叠,使点D落在点B上,点C落在点处,点P为折痕上的任一点,过点P作、 , 垂足分别为G、H,若 , , 求的值;(3)、【迁移拓展】如图 , 在四边形中, , 为边上的一点, , , 垂足分别为D、C, , , , M、N分别为、的中点,连接、 , 求与的周长之和.24. 如图,在边长为的正方形中,过中点E作正 , 过点F的直线分别交边、于点G、H、已知点M、N分别是线段、的动点,且是等边三角形.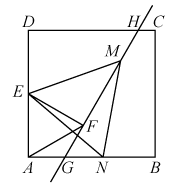 (1)、判断与的位置关系,并说明理由.(2)、当点N在线段上时
(1)、判断与的位置关系,并说明理由.(2)、当点N在线段上时①求证:
②试判断的结果是否变化?若变化,请说明理由;若不变,请求出这个值.
(3)、设 , 点A关于的对称点为 , 若点落在的内部,请直接写出的范围.