浙江省宁波市镇海区2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-02-23 类型:期末考试
一、单选题
-
1. 已知, , 则的值等于( )A、1 B、 C、 D、2. 已知的半径为 , 点P到圆心O的距离为 , 则点( )A、在圆内 B、在圆上 C、在圆外 D、在圆上或圆外3. 抛物线的对称轴是( )A、直线 B、直线 C、直线 D、直线4. 如图,某游乐场一滑梯长为l,滑梯的坡角为 , 那么滑梯的高h的长为( )
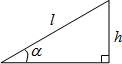 A、 B、 C、 D、5. 如图,的弦长为 , 的半径为 , 则弦的弦心距为( )
A、 B、 C、 D、5. 如图,的弦长为 , 的半径为 , 则弦的弦心距为( )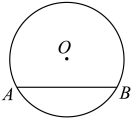 A、 B、 C、 D、6. 如图,已知 , , , 则的长为( )
A、 B、 C、 D、6. 如图,已知 , , , 则的长为( )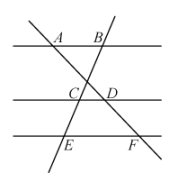 A、2 B、4 C、9 D、107. 将二次函数的图象向左平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )A、 B、 C、 D、8. 如图,是的直径,弦与垂直,垂足为点E,连接并延长交于点 , , , 则图中阴影部分的面积为( )
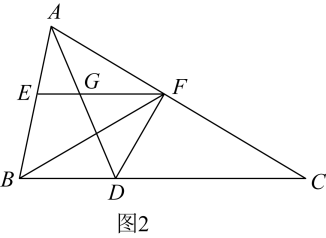
A、2 B、4 C、9 D、107. 将二次函数的图象向左平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )A、 B、 C、 D、8. 如图,是的直径,弦与垂直,垂足为点E,连接并延长交于点 , , , 则图中阴影部分的面积为( ) A、 B、 C、 D、9. 如图,在中,点D、E分别是、的中点,则下列四个结论,其中错误的结论是( )
A、 B、 C、 D、9. 如图,在中,点D、E分别是、的中点,则下列四个结论,其中错误的结论是( )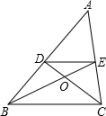 A、 B、 C、 D、10. 如图,是的直径,点C、D在上,且在两侧,于点H交线段于E.若 , , , 则的长为( )
A、 B、 C、 D、10. 如图,是的直径,点C、D在上,且在两侧,于点H交线段于E.若 , , , 则的长为( )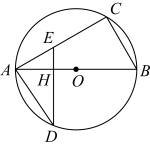 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
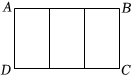
11. 已知线段 , , 则a,b的比例中项线段长等于.12. 一个不透明的口袋中装有红色、黄色、蓝色玻璃球共200个,这些球除颜色外都相同.小明通过大量随机摸球试验后,发现摸到红球的频率稳定在左右,则可估计红球的个数约为.13. 已知为锐角,且 , 则锐角的度数是.14. 如图,把一个大长方形划分成三个全等的小长方形,若每一个小长方形均与大长方形相似,则的值为.
 15. 如图,在的网格图中,每个小正方形的边长均为1.设经过格点A、B、E三点的圆弧与线段交于点D,则弧的弧长为.
15. 如图,在的网格图中,每个小正方形的边长均为1.设经过格点A、B、E三点的圆弧与线段交于点D,则弧的弧长为.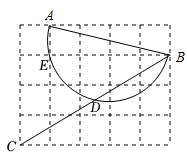 16. 如图,在矩形中, , , 点是对角线上一动点,连接 , 过E作 , 交边于点F,以、为邻边作矩形.
16. 如图,在矩形中, , , 点是对角线上一动点,连接 , 过E作 , 交边于点F,以、为邻边作矩形.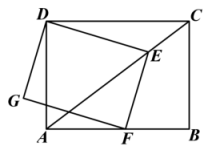 (1)、当时,则的长=.(2)、点在上,且 , 连接 , 则长的最小值是.
(1)、当时,则的长=.(2)、点在上,且 , 连接 , 则长的最小值是.三、解答题
-
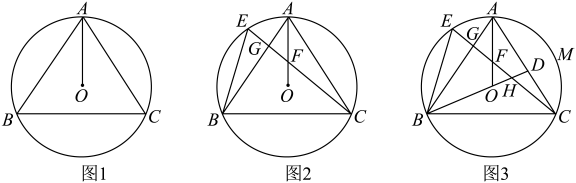
17. 计算:(1)、(2)、已知 , 求的值.18. 一个布袋里装有三个小球,上面分别写着“1”,“2”,“3”,除数字外三个小球无其他差别.(1)、从布袋里任意摸出一个小球,求上面的数字恰好是“3”的概率.(2)、从布袋里任意摸出一个小球,记录其数字,放回并摇匀,再从中任意摸出一个小球,记录其数字,求两次记录的数字之和为3的概率.(要求列表或画树状图说明)19. 如图在的网格中,的顶点都在格点上.仅用无刻度的直尺在给定的网格中分别按下列要求画图.(请保留画图痕迹,画图过程用虚线表示,画图结果用实线表示)
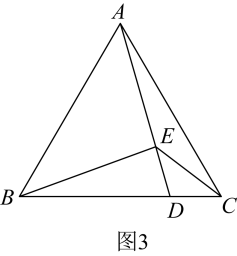
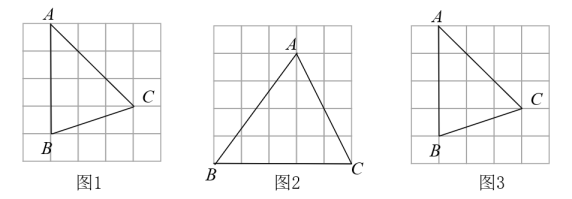 (1)、在图1中,画出的中线和重心G;(2)、在图2中,画线段 , 点E在上,使得;(3)、在图3中,画出的外心点O.20. 在数学综合实践活动课上,某小组要测量学校升旗台旗杆的高度.如图所示,测得BC∥AD,斜坡AB的长为6m,坡度i=1: , 在点B处测得旗杆顶端E的仰角为70°,点B到旗杆底端C的距离为5m.
(1)、在图1中,画出的中线和重心G;(2)、在图2中,画线段 , 点E在上,使得;(3)、在图3中,画出的外心点O.20. 在数学综合实践活动课上,某小组要测量学校升旗台旗杆的高度.如图所示,测得BC∥AD,斜坡AB的长为6m,坡度i=1: , 在点B处测得旗杆顶端E的仰角为70°,点B到旗杆底端C的距离为5m.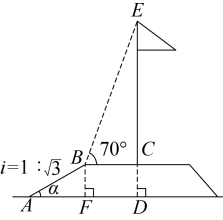 (1)、求斜坡AB的坡角α的度数.(2)、求旗杆顶端离地面的高度ED.(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,结果精确到1m)21. 新华书店销售一个系列的儿童书刊,每套进价100元,销售定价为140元,一天可以销售20套.为了扩大销售,增加盈利,减少库存,书店决定采取降价措施.若一套书每降价1元,平均每天可多售出2套.设每套书降价x元时,书店一天可获利润y元.(1)、求出y与x的函数关系式;(2)、若要书店每天盈利1200元,则每套书销售定价应为多少元?(3)、当每套书销售定价为多少元时,书店一天可获得最大利润?这个最大利润为多少元?22. 如图,在平面直角坐标系中,一次函数的图象与二次函数的图象交于、两点.
(1)、求斜坡AB的坡角α的度数.(2)、求旗杆顶端离地面的高度ED.(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,结果精确到1m)21. 新华书店销售一个系列的儿童书刊,每套进价100元,销售定价为140元,一天可以销售20套.为了扩大销售,增加盈利,减少库存,书店决定采取降价措施.若一套书每降价1元,平均每天可多售出2套.设每套书降价x元时,书店一天可获利润y元.(1)、求出y与x的函数关系式;(2)、若要书店每天盈利1200元,则每套书销售定价应为多少元?(3)、当每套书销售定价为多少元时,书店一天可获得最大利润?这个最大利润为多少元?22. 如图,在平面直角坐标系中,一次函数的图象与二次函数的图象交于、两点. (1)、求与的函数关系式;(2)、直接写出当时,x的取值范围;(3)、点C为一次函数图象上一点,点C的横坐标为n,若将点C向右平移2个单位,再向上平移4个单位后刚好落在二次函数的图象上,求n的值.
(1)、求与的函数关系式;(2)、直接写出当时,x的取值范围;(3)、点C为一次函数图象上一点,点C的横坐标为n,若将点C向右平移2个单位,再向上平移4个单位后刚好落在二次函数的图象上,求n的值.