陕西省渭南市韩城市2022-2023学年九年级上学期学业水平检测试数学试卷
试卷更新日期:2023-02-23 类型:期末考试
一、单选题
-
1. “射击运动员射击一次,命中靶心”这个事件是( )A、必然事件 B、随机事件 C、确定事件 D、不可能事件2. 剪纸是中国最古老的民间艺术之一,其在视觉上给人以透空的感觉和艺术享受.下列剪纸作品中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知四边形ABCD∽四边形EFGH,且AB=3,EF=4,FG=5.则四边形EFGH与四边形ABCD的相似比为( )A、3:4 B、3:5 C、4:3 D、5:34. 如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为 , , .让转盘自由转动,转盘停止后指针(指针指向分隔线,则重新转动转盘)落在红色区域的概率是( )
3. 已知四边形ABCD∽四边形EFGH,且AB=3,EF=4,FG=5.则四边形EFGH与四边形ABCD的相似比为( )A、3:4 B、3:5 C、4:3 D、5:34. 如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为 , , .让转盘自由转动,转盘停止后指针(指针指向分隔线,则重新转动转盘)落在红色区域的概率是( )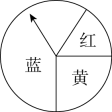 A、 B、 C、 D、5. 若一元二次方程有两个不相等的实数根,则实数a的取值范围为( )A、 B、且 C、且 D、6. 若反比例函数在每个象限内,y随x的增大而减小,则k的值可能是( )A、 B、0 C、 D、17. 如图,四边形内接于 , 是的直径,连接.若 , 则的度数是( )
A、 B、 C、 D、5. 若一元二次方程有两个不相等的实数根,则实数a的取值范围为( )A、 B、且 C、且 D、6. 若反比例函数在每个象限内,y随x的增大而减小,则k的值可能是( )A、 B、0 C、 D、17. 如图,四边形内接于 , 是的直径,连接.若 , 则的度数是( )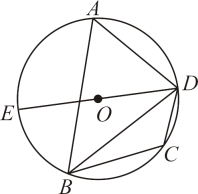 A、 B、 C、 D、8. 将抛物线平移,若有一个点既在平移前的抛物线上,又在平移后的抛物线上,则称这个点为“平衡点”,现将抛物线:向右平移m()个单位长度后得到新的抛物线 , 若为“平衡点”,则m的值为( )A、4 B、3 C、2 D、1
A、 B、 C、 D、8. 将抛物线平移,若有一个点既在平移前的抛物线上,又在平移后的抛物线上,则称这个点为“平衡点”,现将抛物线:向右平移m()个单位长度后得到新的抛物线 , 若为“平衡点”,则m的值为( )A、4 B、3 C、2 D、1二、填空题
-
9. 若一个圆的内接正六边形的边长为2,则这个圆的半径是.10. 如图,已知 , 两条直线分别与、、交于点A、B、C,D、E、F,若 , , , 则的长为.
 11. 一个不透明的箱子里装有a个球,其中红球有5个,这些球除颜色外都相同.每次将箱子里的球搅拌均匀后,任意摸出一个球记下颜色后再放回,大量重复试验后发现,摸到红球的频率稳定在0.25,那么可以估算出a的值为.12. 如图,在平面直角坐标系中,点A在第一象限,轴于点B,反比例函数( , )的图象与线段AB交于点C,且.若的面积为12,则k的值为.
11. 一个不透明的箱子里装有a个球,其中红球有5个,这些球除颜色外都相同.每次将箱子里的球搅拌均匀后,任意摸出一个球记下颜色后再放回,大量重复试验后发现,摸到红球的频率稳定在0.25,那么可以估算出a的值为.12. 如图,在平面直角坐标系中,点A在第一象限,轴于点B,反比例函数( , )的图象与线段AB交于点C,且.若的面积为12,则k的值为.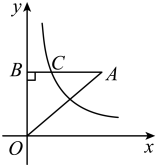 13. 如图,在正方形中, , 为对角线上一动点,为射线上一点,若 , 则的面积的最大值为 .
13. 如图,在正方形中, , 为对角线上一动点,为射线上一点,若 , 则的面积的最大值为 .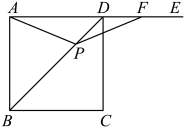
三、解答题
-
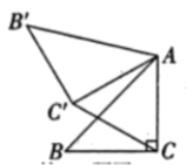
14. 解方程:.15. 如图,在中, , 将绕点A顺时针方向旋转到的位置,连接 , 求的度数.
 16. 已知、是一元二次方程的两个根,求的值.17. 如图,是的直径,点P是上一点,且点P是弦的中点,利用尺规作图法作出弦.(不写作法,保留作图痕迹)
16. 已知、是一元二次方程的两个根,求的值.17. 如图,是的直径,点P是上一点,且点P是弦的中点,利用尺规作图法作出弦.(不写作法,保留作图痕迹) 18. 如图,点D为边上一点,连接 , , , .
18. 如图,点D为边上一点,连接 , , , .求证:.
 19. 如图,在平面直角坐标系中,每个小正方形的边长都是一个单位长度,的顶点都在格点上,点A的坐标是 , 点B的坐标为 , 点C的坐标为.
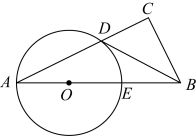
19. 如图,在平面直角坐标系中,每个小正方形的边长都是一个单位长度,的顶点都在格点上,点A的坐标是 , 点B的坐标为 , 点C的坐标为.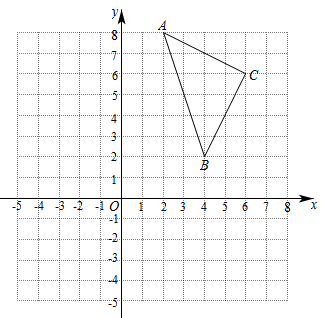 (1)、以O为位似中心,在第三象限内作 , 使与位似,且与的相似比为 , 点A、B、C的对应点分别为、、;(2)、在(1)的条件下,写出点的坐标.20. 韩城历史悠久,夏、商时期以“龙门”代称,某校举行“寻韩城古迹”的社会实践活动.已知学校拟定了4个主题:A司马迁祠,B大禹庙,C党家村,D文庙.小明和小红决定报名参加本次活动,小明从“A司马迁祠,B大禹庙,C党家村”中随机选择一个进行报名,小红从“A司马迁祠,C党家村,D文庙”中随机选择一个进行报名.(1)、小明选中“司马迁祠”的概率是;(2)、请用列表法或树状图法中的一种方法,求小明和小红选中同一个主题的概率.21. 如图,为了估算河的宽度,在河对岸选定一个目标作为点A再在河的这边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.
(1)、以O为位似中心,在第三象限内作 , 使与位似,且与的相似比为 , 点A、B、C的对应点分别为、、;(2)、在(1)的条件下,写出点的坐标.20. 韩城历史悠久,夏、商时期以“龙门”代称,某校举行“寻韩城古迹”的社会实践活动.已知学校拟定了4个主题:A司马迁祠,B大禹庙,C党家村,D文庙.小明和小红决定报名参加本次活动,小明从“A司马迁祠,B大禹庙,C党家村”中随机选择一个进行报名,小红从“A司马迁祠,C党家村,D文庙”中随机选择一个进行报名.(1)、小明选中“司马迁祠”的概率是;(2)、请用列表法或树状图法中的一种方法,求小明和小红选中同一个主题的概率.21. 如图,为了估算河的宽度,在河对岸选定一个目标作为点A再在河的这边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.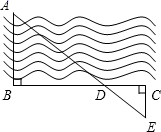 22. 某商店以每个8元的成本价购进了一批玩具陀螺,如果以每个14元的价格出售,那么每天可销售40个,经市场调查发现,若每个陀螺的售价每上涨1元,则每天的销售量就减少2个.每个陀螺涨价多少元时,才能让顾客得到实惠的同时商店每天获得的利润为320元?23. 1896年,挪威生理学家古德贝发现,每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点,这就导致每个人在蒙上眼睛行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈!这就是有趣的“嗐转圈”现象.经研究,某人蒙上眼睛走出的大圆圈的半径y/米是其两腿迈出的步长之差x/厘米()的反比例函数,y与x之间有如表关系:
22. 某商店以每个8元的成本价购进了一批玩具陀螺,如果以每个14元的价格出售,那么每天可销售40个,经市场调查发现,若每个陀螺的售价每上涨1元,则每天的销售量就减少2个.每个陀螺涨价多少元时,才能让顾客得到实惠的同时商店每天获得的利润为320元?23. 1896年,挪威生理学家古德贝发现,每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点,这就导致每个人在蒙上眼睛行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈!这就是有趣的“嗐转圈”现象.经研究,某人蒙上眼睛走出的大圆圈的半径y/米是其两腿迈出的步长之差x/厘米()的反比例函数,y与x之间有如表关系:厘米
1
2
3
5
米
14
7
2.8
请根据表中的信息解决下列问题:
(1)、求出y与x之间的函数解析式;(2)、若某人蒙上眼睛走出的大圆圈的半径为35米,则其两腿迈出的步长之差是多少厘米?24. 跳长绳时,当绳用到最高处时的形状是抛物线,如图正在用绳的两名同学拿绳的手间距为8米,手到地面的距离和均为米,身高为米的小红站在距点O的水平距离为1米的点F处,绳子用到最高处时刚好通过她的头顶点E,以点O为原点建立如图所示的平面直角坐标系,设此抛物线的解析式为.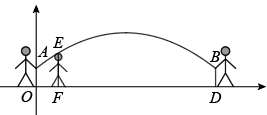 (1)、求该抛物线的解析式;(2)、如果小明站在之间,且离点O的距离为3米,当绳子用到最高处时刚好通过他的头顶正上方米处,求小明的身高是多少?
(1)、求该抛物线的解析式;(2)、如果小明站在之间,且离点O的距离为3米,当绳子用到最高处时刚好通过他的头顶正上方米处,求小明的身高是多少?