江苏省泰州市靖江市2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-02-23 类型:期末考试
一、单选题
-
1. 下列图形是疫情导视标识牌,在这些导视标识牌中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列对于二次函数图象描述中,正确的是( )A、开口向上 B、对称轴是y轴 C、图象有最低点 D、在对称轴右侧的图象从左往右呈上升趋势3. 如图,是直径, , 则∠D为( )
2. 下列对于二次函数图象描述中,正确的是( )A、开口向上 B、对称轴是y轴 C、图象有最低点 D、在对称轴右侧的图象从左往右呈上升趋势3. 如图,是直径, , 则∠D为( )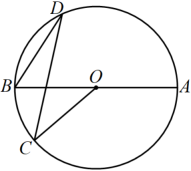 A、 B、 C、 D、4. 如图,线段的两个端点坐标分别为A(2,2)、B(4,2),以原点O为位似中心, 将线段缩小后得到线段 , 若 , 则端点E的坐标为( )
A、 B、 C、 D、4. 如图,线段的两个端点坐标分别为A(2,2)、B(4,2),以原点O为位似中心, 将线段缩小后得到线段 , 若 , 则端点E的坐标为( )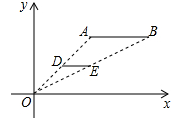 A、(1,1) B、(1,2) C、(2,1) D、(2,2)5. 如图,在正方形网格中:、的顶点都在正方形网格的格点上,则的度数为( )
A、(1,1) B、(1,2) C、(2,1) D、(2,2)5. 如图,在正方形网格中:、的顶点都在正方形网格的格点上,则的度数为( )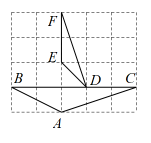 A、 B、 C、 D、6. 已知点 , 在抛物线(m是常数)上,若 , , 则下列大小比较正确的是( )A、 B、 C、 D、
A、 B、 C、 D、6. 已知点 , 在抛物线(m是常数)上,若 , , 则下列大小比较正确的是( )A、 B、 C、 D、二、填空题
-
7. 函数 中自变量x的取值范围是 .8. 已知关于的一元二次方程有两个实数根、 , 且 , 则.9. 已知线段AB=10cm,点C是 线段AB的黄金分割点,(AC>BC)则AC的长是 .10. 已知抛物线的顶点在y轴上,则k的值是.11. 有块余料是直角三角形.两直角边长为6和8,在该余料中剪一个圆,剪得圆面积最大为.12. 在2×2的正方形网格中,每个小正方形的边长为1.以点O为圆心,2为半径画弧,交图中网格线于点A,B,则扇形AOB的面积是.
 13. 一个圆锥的高为 , 其侧面展开图是半圆,则圆锥的面积是14. 如图,将一个等腰的直角顶点C放在上,绕点C旋转三角形,使边经过圆心O,某一时刻,斜边在上截得的线段cm,且cm,的长为cm.
13. 一个圆锥的高为 , 其侧面展开图是半圆,则圆锥的面积是14. 如图,将一个等腰的直角顶点C放在上,绕点C旋转三角形,使边经过圆心O,某一时刻,斜边在上截得的线段cm,且cm,的长为cm.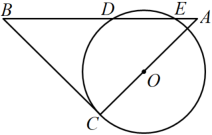 15. 二次函数图像的一部分如图所示,下列结论:①;②;③有两个相等的实数根;④.其中正确的为(只填序号).
15. 二次函数图像的一部分如图所示,下列结论:①;②;③有两个相等的实数根;④.其中正确的为(只填序号).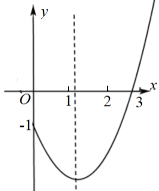 16. 如图.在正方形ABCD中,边长为4,M是CD的中点,点P是BC上一个动点,当∠DPM的度数最大时,则BP=.
16. 如图.在正方形ABCD中,边长为4,M是CD的中点,点P是BC上一个动点,当∠DPM的度数最大时,则BP=.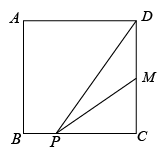
三、解答题
-
17.(1)、计算:;(2)、解方程:.18. 先化简再求值: , 其中a是方程的根.19. 已知二次函数(b,c为常数)的图像经过点.
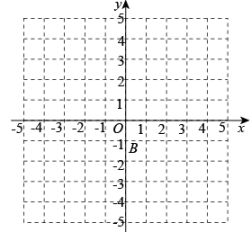 (1)、直接填空:b= , c= ;(2)、图中的网格由边长为1的小正方形组成,在所给坐标系中画出该二次函数图象;(3)、根据图像,当时,y的取值范围是.20. 如图,已知P是⊙O上一点,用两种不同的方法过点P作⊙O的一条切线.
(1)、直接填空:b= , c= ;(2)、图中的网格由边长为1的小正方形组成,在所给坐标系中画出该二次函数图象;(3)、根据图像,当时,y的取值范围是.20. 如图,已知P是⊙O上一点,用两种不同的方法过点P作⊙O的一条切线.要求:

 (1)、用直尺和圆规作图;(2)、保留作图痕迹,写出必要的文字说明.21. 如图,已知四边形内接于.求证:.
(1)、用直尺和圆规作图;(2)、保留作图痕迹,写出必要的文字说明.21. 如图,已知四边形内接于.求证:.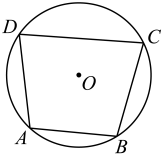 22. 自新冠疫情防控“新十条”发布以来,市场上对日常居民所用消毒液的需求量日益加大,某消毒液厂为满足市场需求,改造了10条消毒液生产线,每条生产线每天可生产消毒液300吨.由于人员和资金限制,如果每增加一条生产线,每条生产线每天就会少生产20吨消毒液.设增加x条生产线(x为正整数),每条生产线每天可生产消毒液y吨(1)、y与x之间的函数关系式为;(2)、设该厂每天可以生产消毒液w吨,请求出w与x的函数关系式,并求出当x为多少时,每天生产的消毒液最多?最多为多少吨?23. 某建筑工地的平衡力矩塔吊如图所示,在配重点E处测得塔帽A的仰角为 , 在点E的正下方米处的点D处测得塔帽A的仰角为 , 请你依据相关数据计算塔帽与地面的距离的高度.(计算结果精确到米,参考数据: , , , )
22. 自新冠疫情防控“新十条”发布以来,市场上对日常居民所用消毒液的需求量日益加大,某消毒液厂为满足市场需求,改造了10条消毒液生产线,每条生产线每天可生产消毒液300吨.由于人员和资金限制,如果每增加一条生产线,每条生产线每天就会少生产20吨消毒液.设增加x条生产线(x为正整数),每条生产线每天可生产消毒液y吨(1)、y与x之间的函数关系式为;(2)、设该厂每天可以生产消毒液w吨,请求出w与x的函数关系式,并求出当x为多少时,每天生产的消毒液最多?最多为多少吨?23. 某建筑工地的平衡力矩塔吊如图所示,在配重点E处测得塔帽A的仰角为 , 在点E的正下方米处的点D处测得塔帽A的仰角为 , 请你依据相关数据计算塔帽与地面的距离的高度.(计算结果精确到米,参考数据: , , , )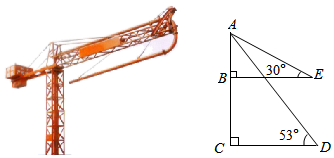 24. 如图,已知中, , , 点D、E在边上,.
24. 如图,已知中, , , 点D、E在边上,.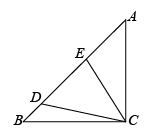 (1)、求证:;(2)、当 , 时,求的长.25. 如图,抛物线与x轴交于点A和点B,与y轴交于点C.
(1)、求证:;(2)、当 , 时,求的长.25. 如图,抛物线与x轴交于点A和点B,与y轴交于点C. (1)、求出A、B、C三点的坐标;(2)、将抛物线图像x轴上方部分沿x轴向下翻折,保留抛物线与x轴的交点和x轴下方图像,得到的新图像记作M,图像M与直线恒有四个交点,从左到右四个交点依次记为D,E,F,G.若以为直径作圆,该圆记作图像N.
(1)、求出A、B、C三点的坐标;(2)、将抛物线图像x轴上方部分沿x轴向下翻折,保留抛物线与x轴的交点和x轴下方图像,得到的新图像记作M,图像M与直线恒有四个交点,从左到右四个交点依次记为D,E,F,G.若以为直径作圆,该圆记作图像N.①在图像M上找一点P,使得的面积为3,求出点P的坐标;
②当图像N与x轴相离时,直接写出t的取值范围.
26. 小明在学习了《圆周角定理及其推论》后,有这样的学习体会:在中, , 当长度不变时.则点C在以为直径的圆上运动(不与A、B重合).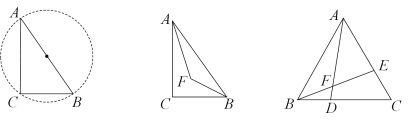 (1)、【探索发现】
(1)、【探索发现】小明继续探究,在中, , 长度不变.作与的角平分线交于点F,小明计算后发现的度数为定值,小明猜想点F也在一个圆上运动.请你计算的度数,并简要说明小明猜想的圆的特征.
(2)、【拓展应用】
在【探索发现】的条件下,若 , 求出面积的最大值.(3)、【灵活运用】
在等边中, , 点D、点E分别在和边上,且 , 连接交于点F,试求出周长的最大值.