江西省抚州市2023年中考一模数学试卷
试卷更新日期:2023-02-23 类型:中考模拟
一、单选题
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 以下说法合理的是( )A、小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是 B、某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖 C、某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是 D、小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是3. 在七年级的学习中,我们知道了 .小明同学突发奇想,画出了函数 的图像,你认为正确的是( )A、
2. 以下说法合理的是( )A、小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是 B、某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖 C、某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是 D、小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是3. 在七年级的学习中,我们知道了 .小明同学突发奇想,画出了函数 的图像,你认为正确的是( )A、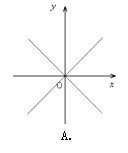 B、
B、 C、
C、 D、
D、 4. 如图,已知点A,B,C,D,E是⊙O的五等分点,则∠BAD的度数是( )
4. 如图,已知点A,B,C,D,E是⊙O的五等分点,则∠BAD的度数是( )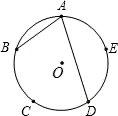 A、36° B、48° C、72° D、96°5. 如图,中, , 点O是边上的一点,与分别相切于点A、E,点F为上一点,连 , 若四边形是菱形,则图中阴影部分面积是( )
A、36° B、48° C、72° D、96°5. 如图,中, , 点O是边上的一点,与分别相切于点A、E,点F为上一点,连 , 若四边形是菱形,则图中阴影部分面积是( ) A、 B、 C、 D、6. 把二次三项式2x2﹣8xy+5y2因式分解,下列结果中正确的是( )A、(x﹣ y)(x﹣ y) B、(2x﹣4y+ y)(x﹣ y) C、(2x﹣4y+ y)(x﹣ y) D、2(x﹣ y)(x﹣ y)
A、 B、 C、 D、6. 把二次三项式2x2﹣8xy+5y2因式分解,下列结果中正确的是( )A、(x﹣ y)(x﹣ y) B、(2x﹣4y+ y)(x﹣ y) C、(2x﹣4y+ y)(x﹣ y) D、2(x﹣ y)(x﹣ y)二、填空题
-
7. 已知关于x的方程x2-2x+2k-1=0的两根分别是x1、x2 , 且x1·x2 , 则k的值是 .8. 反比例函数(x<0)图象上的点的函数值y随x增大而 (填“增大”或“减小”).9.
蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有 .
 10. 化简:的结果是 .11. 抛物线的顶点坐标为 .12. 如图,长方形 ABCD 中,点 E 在边 AB 上,将一边 AD 折叠,使点 A恰好落在边 BC 的点 F 处,折痕为 DE.若 AB=4,BF=2,则 AE的长是 .
10. 化简:的结果是 .11. 抛物线的顶点坐标为 .12. 如图,长方形 ABCD 中,点 E 在边 AB 上,将一边 AD 折叠,使点 A恰好落在边 BC 的点 F 处,折痕为 DE.若 AB=4,BF=2,则 AE的长是 .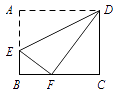
三、解答题
-
13. 用适当的方法解下列一元二次方程:(1)、(x﹣1)2=2;(2)、2x2+5x=﹣214. 若抛物线y=2x2+bx+c的顶点坐标M(2,-2),求:抛物线与x轴交点的坐标.15. 我校九(1)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如表(10分制):
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9
(1)、甲队成绩的中位数是分,乙队成绩的平均数是分;(2)、已知甲队成绩的方差是1.4分,则成绩较为整齐的是队;(3)、测试结果中,乙队获满分的四名同学相当优秀,他们是三名男生、一名女生,现准备从这四名同学中随机抽取两人参加学校组织的经典诵读比赛,求恰好抽中一男生一女生的概率.16. 已知实数 , , 在数轴上的位置如图所示,化简: .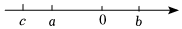 17. 如图,已知中,以为直径的⊙交于 , 交于 , , 求的度数.
17. 如图,已知中,以为直径的⊙交于 , 交于 , , 求的度数. 18. 如图,一次函数y=x+1的图象与反比例函数的图象交于点 .
18. 如图,一次函数y=x+1的图象与反比例函数的图象交于点 . (1)、求反比例函数的解析式;(2)、点也在反比例函数图象上,求△DOB的面积.19. 如图:已知 , , 平分 .
(1)、求反比例函数的解析式;(2)、点也在反比例函数图象上,求△DOB的面积.19. 如图:已知 , , 平分 . (1)、与平行吗?说明理由.(2)、与的位置关系如何?为什么?(3)、平分吗?为什么?20. 某超市经销一种商品,每千克成本为30元,经试销发现,该种食品的每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:
(1)、与平行吗?说明理由.(2)、与的位置关系如何?为什么?(3)、平分吗?为什么?20. 某超市经销一种商品,每千克成本为30元,经试销发现,该种食品的每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:销售单价x(元/千克)
40
45
55
60
销售量y(千克)
80
70
50
40
(1)、求y(千克)与x(元/千克)之间的函数表达式;(2)、若商店按销售单价不低于成本价,且不高于60元的价格销售,要使销售该商品每天获得的利润为800元,求每天的销售量应为多少千克?21. 已知抛物线的对称轴为 .(1)、求m的值;(2)、如果将此抛物线先向左平移2个单位,再向下平移1个单位,求两次平移后所得到的抛物线表达式.22. 如图,为的直径,为弦的中点,连接并延长交于点 , 过点作∥ , 交的延长线于点 , 连接 , . (1)、求证:是⊙的切线;(2)、若时,
(1)、求证:是⊙的切线;(2)、若时,①求图中阴影部分的面积;
②以为原点,所在的直线为轴,直径的垂直平分线为轴,建立如图所示的平面直角坐标系,试在线段上求一点 , 使得直线把阴影部分的面积分成的两部分.
23. 旋转变换在平面几何中有着广泛的应用.特别是在解(证)有关等腰三角形、正三角形、正方形等问题时,更是经常用到的思维方法,请你用旋转交换等知识,解决下面的问题.如图1,△ABC与△DCE均为等腰直角三角形,DC与AB交于点M,CE与AB交于点N.
 (1)、以点C为中心,将△ACM逆时针旋转90°,画出旋转后的△A′CM′(2)、在(1)的基础上,证明AM2+BN2=MN2 .(3)、如图2,在四边形ABCD中,∠BAD=45°,∠BCD=90°,AC平分∠BCD,若BC=4,CD=3,则对角线AC的长度为多少?(直接写出结果即可,但在图中保留解决问题的过程中所作辅助线、标记的有关计算数据等)
(1)、以点C为中心,将△ACM逆时针旋转90°,画出旋转后的△A′CM′(2)、在(1)的基础上,证明AM2+BN2=MN2 .(3)、如图2,在四边形ABCD中,∠BAD=45°,∠BCD=90°,AC平分∠BCD,若BC=4,CD=3,则对角线AC的长度为多少?(直接写出结果即可,但在图中保留解决问题的过程中所作辅助线、标记的有关计算数据等)