安徽省宿州市萧县2023年一模数学试题
试卷更新日期:2023-02-23 类型:中考模拟
一、单选题
-
1. 下列各点中,在反比例函数图象上的点是( )A、 B、 C、 D、2. 下图是由6个相同的小正方体组成的几何体,其俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 两个三角形相似比是3:4,其中小三角形的周长为9,则另一个大三角形的周长是( )A、12 B、16 C、27 D、364. 如图,点D在的边上,添加一个条件,使得 , 下列错误的是( )
3. 两个三角形相似比是3:4,其中小三角形的周长为9,则另一个大三角形的周长是( )A、12 B、16 C、27 D、364. 如图,点D在的边上,添加一个条件,使得 , 下列错误的是( )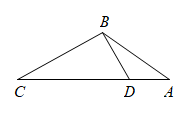 A、 B、 C、 D、5. 如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为光源,到屏幕的距离为 , 且幻灯片中图形的高度为 , 则屏幕上图形的高度为( )
A、 B、 C、 D、5. 如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为光源,到屏幕的距离为 , 且幻灯片中图形的高度为 , 则屏幕上图形的高度为( ) A、 B、 C、 D、6. 如图,五线谱是由等距离,等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段 , 则线段的长是( )
A、 B、 C、 D、6. 如图,五线谱是由等距离,等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段 , 则线段的长是( ) A、 B、1 C、 D、37. 已知函数的图象经过点 , , 如果 , 那么( )A、 B、 C、 D、8. 如图,四边形与四边形位似,其位似中心为点O,且 , 则四边形的面积与四边形的面积之比为( )
A、 B、1 C、 D、37. 已知函数的图象经过点 , , 如果 , 那么( )A、 B、 C、 D、8. 如图,四边形与四边形位似,其位似中心为点O,且 , 则四边形的面积与四边形的面积之比为( ) A、 B、 C、 D、9. 一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现,如图所示的是该台灯的电流I(A)与电阻R()成反比例函数的图象,该图象经过点 . 根据图象可知,下列说法正确的是( )
A、 B、 C、 D、9. 一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现,如图所示的是该台灯的电流I(A)与电阻R()成反比例函数的图象,该图象经过点 . 根据图象可知,下列说法正确的是( )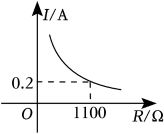 A、I与R的函数关系式是 B、当时, C、当时, D、当电阻R()越大时,该台灯的电流I(A)也越大10. 如图,在中,平分交于点C,平分交OA于点D,交于点E,反比例函数 , 经过点E,若 , , 则k的值为( )
A、I与R的函数关系式是 B、当时, C、当时, D、当电阻R()越大时,该台灯的电流I(A)也越大10. 如图,在中,平分交于点C,平分交OA于点D,交于点E,反比例函数 , 经过点E,若 , , 则k的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,若反比例函数的图像经过点A,轴于B,且的面积为3,则k的值为 .
 12. 如图,在平面直角坐标系中,点光源位于处,木杆两端的坐标分别为 , . 则木杆在x轴上的影长为 .
12. 如图,在平面直角坐标系中,点光源位于处,木杆两端的坐标分别为 , . 则木杆在x轴上的影长为 . 13. 在正方形网格中,每个小正方形的顶点称为格点.如图,点均在格点上,连接相交于点 , 若小正方形的边长为1,则点到的距离为 .
13. 在正方形网格中,每个小正方形的顶点称为格点.如图,点均在格点上,连接相交于点 , 若小正方形的边长为1,则点到的距离为 . 14. 如图,在中, , 分别以 , 为边向外作正方形和正方形 , 连接 , , 分别交 , 于点M,N,已知 , .
14. 如图,在中, , 分别以 , 为边向外作正方形和正方形 , 连接 , , 分别交 , 于点M,N,已知 , .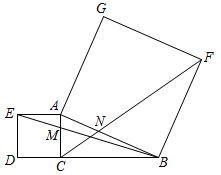 (1)、AB= .(2)、CF= .
(1)、AB= .(2)、CF= .三、解答题
-
15. 下图是一个几何体的三视图,其中俯视图为正三角形.
 (1)、这个几何体的名称为 .(2)、求该几何体的左视图中a的值.16. 在平面直角坐标系内,的位置如图所示.
(1)、这个几何体的名称为 .(2)、求该几何体的左视图中a的值.16. 在平面直角坐标系内,的位置如图所示.
⑴将绕点O顺时针旋转得到 , 作出 .
⑵以原点O为位似中心,在第四象限内作出的位似图形 , 且与的相似比为 .
17. 在践行“安全在我心中,你我一起行动”主题手抄报评比活动中,共设置了“交通安全、消防安全、饮食安全、防疫安全”四个主题内容,推荐子航和紫琪两名学生参加评比,若他们每人从以上四个主题内容中随机选择一个,每个主题被选择的可能性相同. (1)、子航选择交通安全手抄报的概率为;(2)、求子航和紫琪选择同一主题手抄报的概率.(用树状图或列表法求解)18. 为检测某品牌一次性注射器的质量,将注射器里充满一定量的气体,当温度不变时,注射器里的气体的压强与气体体积满足反比例函数关系,其图像如图所示.
(1)、子航选择交通安全手抄报的概率为;(2)、求子航和紫琪选择同一主题手抄报的概率.(用树状图或列表法求解)18. 为检测某品牌一次性注射器的质量,将注射器里充满一定量的气体,当温度不变时,注射器里的气体的压强与气体体积满足反比例函数关系,其图像如图所示.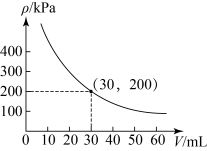 (1)、求反比例函数的表达式.(2)、当气体体积为60ml时,气体的压强为kPa.(3)、若注射器内气体的压强不能超过500kPa,则其体积V要控制在什么范围?19. 观察下图中用小黑点摆成的三角形,并根据图中规律回答相关问题.
(1)、求反比例函数的表达式.(2)、当气体体积为60ml时,气体的压强为kPa.(3)、若注射器内气体的压强不能超过500kPa,则其体积V要控制在什么范围?19. 观察下图中用小黑点摆成的三角形,并根据图中规律回答相关问题. (1)、第4个图形对应的等式为 .(2)、若第n个图形对应的黑点总数为66个,求n的值.20. 如图,反比例函数的图像与正比例函数的图像相交于 , C两点.
(1)、第4个图形对应的等式为 .(2)、若第n个图形对应的黑点总数为66个,求n的值.20. 如图,反比例函数的图像与正比例函数的图像相交于 , C两点.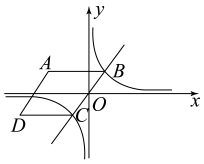 (1)、求k的值及B点的坐标.(2)、不等式的解集为 .(3)、已知轴,以、为边作菱形 , 求菱形的面积.21. 某超市以每千克40元的价格购进菠萝蜜,计划以每千克60元的价格销售,为了让顾客得到实惠,现决定降价销售,已知这种菠萝蜜销售量y(千克)与每千克降价x(元)()之间满足一次函数关系,其图像如图所示.
(1)、求k的值及B点的坐标.(2)、不等式的解集为 .(3)、已知轴,以、为边作菱形 , 求菱形的面积.21. 某超市以每千克40元的价格购进菠萝蜜,计划以每千克60元的价格销售,为了让顾客得到实惠,现决定降价销售,已知这种菠萝蜜销售量y(千克)与每千克降价x(元)()之间满足一次函数关系,其图像如图所示.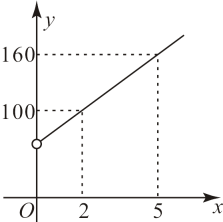 (1)、求y与x之间的函数关系式.(2)、当每千克菠萝蜜降价4元时,超市获利多少元?(3)、若超市要想获利2400元,且让顾客获得更大实惠,这种菠萝蜜每千克应降价多少元?22. 我国古代数学家赵爽利用影子对物体进行测量的方法,至今仍有借鉴意义.如图1,身高的小王晚上在路灯灯柱下散步,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部A向东走20步到M处,发现自己的影子端点落在点P处,作好记号后,继续沿刚才自己的影子走4步恰好到达点P处,此时影子的端点在点Q处,已知小王和灯柱的底端在同一水平线上,小王的步间距保持一致.
(1)、求y与x之间的函数关系式.(2)、当每千克菠萝蜜降价4元时,超市获利多少元?(3)、若超市要想获利2400元,且让顾客获得更大实惠,这种菠萝蜜每千克应降价多少元?22. 我国古代数学家赵爽利用影子对物体进行测量的方法,至今仍有借鉴意义.如图1,身高的小王晚上在路灯灯柱下散步,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部A向东走20步到M处,发现自己的影子端点落在点P处,作好记号后,继续沿刚才自己的影子走4步恰好到达点P处,此时影子的端点在点Q处,已知小王和灯柱的底端在同一水平线上,小王的步间距保持一致.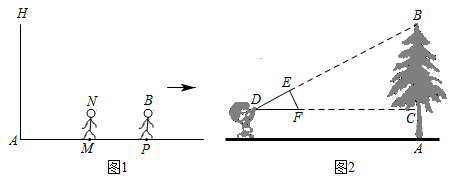 (1)、请在图中画出路灯O和影子端点Q的位置.(2)、估计路灯的高,并求影长的步数.(3)、无论点光源还是视线,其本质是相同的,日常生活中我们也可以直接利用视线解决问题.如图2,小明同学用自制的直角三角形纸板测量树的高度 , 他调整自己的位置,设法使斜边保持水平,并且边与点B在同一直线上.测得 , , , 小明眼睛到地面的距离为 , 则树高为m.23. 如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为 , 分别落在x轴和y轴上,将绕点O逆时针旋转,使点B落在y轴上,得到 , 与相交于点F,反比例函数的图象经过点F,交于点G.
(1)、请在图中画出路灯O和影子端点Q的位置.(2)、估计路灯的高,并求影长的步数.(3)、无论点光源还是视线,其本质是相同的,日常生活中我们也可以直接利用视线解决问题.如图2,小明同学用自制的直角三角形纸板测量树的高度 , 他调整自己的位置,设法使斜边保持水平,并且边与点B在同一直线上.测得 , , , 小明眼睛到地面的距离为 , 则树高为m.23. 如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为 , 分别落在x轴和y轴上,将绕点O逆时针旋转,使点B落在y轴上,得到 , 与相交于点F,反比例函数的图象经过点F,交于点G.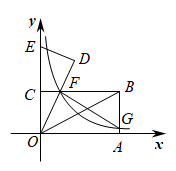 (1)、求k的值.(2)、连接 , 则图中是否存在与相似的三角形?若存在,请把它们一一找出来,并选其中一种进行证明;若不存在,请说明理由.(3)、点M在直线上,N是平面内一点,当四边形是正方形时,请直接写出点N的坐标.
(1)、求k的值.(2)、连接 , 则图中是否存在与相似的三角形?若存在,请把它们一一找出来,并选其中一种进行证明;若不存在,请说明理由.(3)、点M在直线上,N是平面内一点,当四边形是正方形时,请直接写出点N的坐标.