初中数学同步训练必刷题（人教版八年级下册第十八章平行四边形全章测试卷）

试卷更新日期：2023-02-22 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列命题是真命题的是（）

A、对边相等的四边形是平行四边形 B、有一个角是90°的平行四边形是矩形 C、邻边相等的四边形是菱形 D、对角线互相垂直的平行四边形为正方形

查看试题解析
2. 如图，矩形 $A B C D$ 中，对角线 $A C 、 B D$ 交于点O，若 $∠ A O B = 60 °$ ， $B D = 8$ ，则 $D C$ 长为（）

A、 $4 \sqrt{3}$ B、4 C、3 D、5

查看试题解析
3. 如果三角形的两边分别为3和5，那么连结这个三角形三边中点所得三角形的周长可能是（）

A、5.5 B、5 C、4.5 D、4

查看试题解析
4. 如图，面积为3的正方形 $A B C D$ 的顶点 $A$ 在数轴上，且表示的数为 $- 1$ ，若 $A D = A E$ ，则数轴上点 $E$ 所表示的数为（）

A、 $\sqrt{3} - 1$ B、 $\sqrt{3} + 1$ C、 $- \sqrt{3} + 1$ D、 $\sqrt{3}$

查看试题解析
5. 已知菱形的面积为 $120 c m^{2}$ ，一条对角线长为 $10 c m$ ，则它的边长为（）

A、 $10 c m$ B、 $12 c m$ C、 $13 c m$ D、 $15 c m$

查看试题解析
6. 如图，在矩形 $A B C D$ 中， $A C$ ， $B D$ 相交于点 $O$ ， $A E$ 平分 $∠ B A D$ 交 $B C$ 于 $E$ ，若 $∠ E A O = 1 5^{∘}$ ，则 $∠ B O E$ 的度数为（）

A、 $8 5^{∘}$ B、 $8 0^{∘}$ C、 $7 5^{∘}$ D、 $7 0^{∘}$

查看试题解析
7. 如图，点F为正方形 $A B C D$ 对角线 $A C$ 的中点，将以点F为直角顶点的直角 $△ F E G$ 绕点F旋转（ $△ F E G$ 的边EG始终在正方形 $A B C D$ 外），若正方形 $A B C D$ 边长为3，则在旋转过程中 $△ F E G$ 与正方形 $A B C D$ 重叠部分的面积为（）

A、9 B、3 C、4.5 D、2.25

查看试题解析
8. 如图，点E、F、G、H分别是四边形ABCD四条边的中点，要使四边形EFGH为菱形，四边形ABCD应具备的条件是（）

A、一组对边平行而另一组对边不平行 B、对角线相等 C、对角线互相垂直 D、对角线互相平分

查看试题解析
9. 如图，矩形ABCD中，AC、BD交于点O，M、N分别为BC、OC的中点．若 $∠ A C B = 3 0^{°}$ ， $A B = 10$ ，则MN的长为（）

A、 $5 \sqrt{2}$ B、5 C、 $5 \sqrt{3}$ D、4

查看试题解析
10. 如图，菱形ABCD中，∠BAD＝60°，AC、BD交于点O，E为CD延长线上的一点，且CD＝DE，连接BE分别交AC，AD于点F、G，连接OG、AE.则下列结论：①OG＝ $\frac{1}{2}$ AB； ②四边形ABDE是菱形；③S_四边形_ODGF＝S_△_ABF；其中正确的是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析

二、填空题(每题3分，共24分）

11. 如图，若将四根木条钉成的矩形木框ABCD变形为平行四边形A′BCD′，并使其面积为矩形ABCD面积的一半，若A′D′与CD交于点E，且AB＝2，则△ECD′的面积是.

查看试题解析
12. 已知 $a = 3$ ， $b = 4$ ，那么以a、b为边长的直角三角形斜边上的中线长为 .

查看试题解析
13. 如图，长方形 $A B C D$ 中， $A B = 6 ， A D = 12$ ， E为 $B C$ 边上的动点，F为 $C D$ 的中点，连接 $A E ， E F$ ，则 $A E + E F$ 的最小值为

查看试题解析
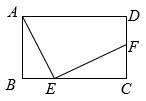14. 如图，在长方形ABCD中，AB＝8，GC＝ $\frac{9}{8}$ ， AE平分∠BAG交BC于点E，E是BC的中点，则AG的长为.

查看试题解析
15. 如图，矩形 $A B C D$ 的对角线 $A C 、 B D$ 交于点O， $A B = 6 ， B C = 8$ ，过点O作 $O E ⊥ A C$ ，交AD于点E，过点E作 $E F ⊥ B D$ ，垂足为F，则 $O E + E F$ 的值为.

查看试题解析
16. 如图，菱形ABCD的对角线AC，BD相交于点O，过点D作 $D H ⊥ A B$ 于点H，连接OH，若 $O A = 4$ ， $O H = 2$ ，则菱形ABCD的面积为．

查看试题解析
17. 如图，在给定的一张平行四边形 $A B C D$ 纸片上，用尺规作出四边形 $A B E F$ ，具体作法如下：分别作 $∠ A ， ∠ B$ 的平分线 $A E ， B F$ ，分别交 $B C ， A D$ 于 $E ， F$ ，连接 $E F$ ，若 $A E = 6 ， B F = 8$ ，则四边形 $A B E F$ 的周长是．

查看试题解析
18. 如图，在正方形 $A B C D$ 中，E为 $A D$ 的中点，F为 $A B$ 的中点， $D F$ 的延长线与 $C B$ 的延长线交于点H， $C E$ 与 $D H$ 相交于点G，若 $A B = 10$ ，则 $B G$ 的长为．

查看试题解析

三、解答题（共6题，共66分）

19. 如图，四边形 $A B C D$ 是平行四边形， $B E // D F$ 且分别交对角线 $A C$ 于点E ， F ．

(1)、求证： $△ A B E ≌ △ C D F$ ；

(2)、当四边形 $A B C D$ 分别是矩形和菱形时，请分别说出四边形 $B E D F$ 的形状．（无需说明理由）

查看试题解析
20. 在 $▱ A B C D$ 中，E、F分别是边BC，AD的中点，AC是对角线，过点D作DP $∥$ AC，交BA的延长线于点P，∠P=90°．求证：四边形AECF是菱形．

查看试题解析
21. 如图，E是正方形ABCD对角线BD上一点，连接AE，CE，并延长CE交AD于点F．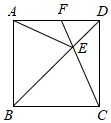

(1)、求证：△ABE≌△CBE；

(2)、若∠AEC＝140°，求∠DFE的度数．

查看试题解析
22. 如，在矩形ABCD中，AB=16 cm，AD=6 cm，动点P，Q分别从点A，C同时出发，点P以每秒3 cm的速度向点B移动，点Q以每秒2 cm的速度向点D移动，当点P到达点B时，两点均停止移动.是否存在某一时刻，使四边形PBCQ为正方形?若存在，求出该时刻；若不存在，请说明理由.

查看试题解析
23. 如图，四边形 $A B C D$ 是菱形，对角线 $A C$ 和 $B D$ 相交于点O、点E是 $C D$ 的中点，过点C作 $A C$ 的垂线，与 $O E$ 的延长线交于点F，连接 $F D$ .

(1)、求证：四边形 $O C F D$ 是矩形；

(2)、若四边形 $A B C D$ 的周长为 $4 \sqrt{5}$ ， $△ A O B$ 的周长为 $3 + \sqrt{5}$ ，求四边形 $O C F D$ 的面积；

(3)、在（2）问的条件下， $B D$ 上有一动点Q， $C D$ 上有一动点P，求 $P Q + Q E$ 的最小值.

查看试题解析
24. 如图1，在△ABC中，AB＝AC，∠ABC＝ɑ，D是BC边上一点，以AD为边作△ADE，使AE＝AD，∠DAE+∠BAC＝180°．

(1)、若α＝46°，求∠ADE的度数；

(2)、以AB、AE为边作平行四边形ABFE．
①如图2，若点F恰好落在DE上．求证：BD＝CD；
②如图3，若点F恰好落在BC上．求证：BD＝CF．

查看试题解析

初中数学同步训练必刷题（人教版八年级下册 第十八章 平行四边形 全章测试卷）

一、单选题（每题3分，共30分）

二、填空题(每题3分，共24分）

三、解答题（共6题，共66分）

初中数学同步训练必刷题（人教版八年级下册第十八章平行四边形全章测试卷）