吉林省松原市乾安县2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-02-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式中，正确的是（）

A、 $\sqrt{16} = \pm 4$ B、 $\sqrt[3]{- 27} = - 3$ C、 $- \sqrt{16} = 4$ D、 $\sqrt{{(- 4)}^{2}} = - 4$

查看试题解析
2. 如图，一把长方形直尺沿直线断开并错位，点E、D、B、F在同一条直线上，若∠ADE=125°，则∠DBC的度数为（）

A、55° B、65° C、75° D、125°

查看试题解析
3. 点P为直线 $M N$ 外一点，点A、B、C为直线 $M N$ 上三点， $P A = 4 c m$ ， $P B = 5 c m$ ， $P C = 2 c m$ ，则P到直线 $M N$ 的距离为（）

A、 $4 c m$ B、 $2 c m$ C、小于 $2 c m$ D、不大于 $2 c m$

查看试题解析
4. 把点P₁（2，-3）向右平移3个单位长度再向下平移2个单位长度到达点P₂处，则P₂的坐标是（　　）

A、（5，－1） B、（－1，－5） C、（5，－5） D、（－1，－1）

查看试题解析
5. 以下方程中，是二元一次方程的是（）

A、 $8 x - y = y$ B、 $xy = 3$ C、 $3 x + 2 y = 3 z$ D、 $y = \frac{1}{x}$

查看试题解析
6. 将一张面值100元的人民币，兑换成10元或20元的零钱，兑换方案有（）

A、4种 B、5种 C、6种 D、7种

查看试题解析

二、填空题

7. 化简： $\sqrt{64} =$ ．

查看试题解析
8. 在平面直角坐标系中，点A（﹣3，4）在第象限．

查看试题解析
9. 若方程组 ${\begin{matrix} x = y + 5 \\ 2 x - y = 5 \end{matrix}$ 的解满足方程 $x + y + a = 0$ ，则a的值为.

查看试题解析
10. 有一个英文单词的字母顺序对应如图中的有序数对分别为（5，3），（6，3）（7，3）（4，1）（4，4）请你把这个英文单词写出来或者翻译中文为．

查看试题解析
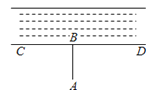
11.
如图，计划把河水引到水池A中，先作AB⊥CD，垂足为B，然后沿AB开渠，能使所开的渠道最短，这样设计的依据是

查看试题解析
12. 如图是一块长方形ABCD的场地，长AB＝102 m，宽AD＝51 m，从A，B两处入口的路宽都为1 m，两小路汇合处路宽为2 m，其余部分种植草坪，则草坪的面积为m².

查看试题解析
13. 如图，把一张长方形纸条 $A B C D$ 沿 $A F$ 折叠，点B对应点E，已知 $∠ A D B = 20 °$ ，当 $A E ∥ B D$ 时， $∠ B A F$ 的度数为°．

查看试题解析
14. 观察下列各式： $\sqrt{1 + \frac{1}{3}} = 2 \sqrt{\frac{1}{3}}$ ， $\sqrt{2 + \frac{1}{4}} = 3 \sqrt{\frac{1}{4}}$ ， $\sqrt{3 + \frac{1}{5}} = 4 \sqrt{\frac{1}{5}}$ ，…,根据你发现的规律，若式子 $\sqrt{a + \frac{1}{b}} = 8 \sqrt{\frac{1}{b}}$ (a、b为正整数)符合以上规律，则 $\sqrt{a + b}$ =.

查看试题解析

三、解答题

15.

(1)、计算： $| \sqrt{3} - 2 | - \sqrt[3]{- 27} - \sqrt{{(- 2)}^{2}}$

(2)、解方程： ${(x - 5)}^{3} + 8 = 0$ ．

查看试题解析
16. 解方程组 ${\begin{matrix} x - y = 8 \\ 3 x + y = 12 \end{matrix}$ ．

查看试题解析
17. 已知 $A (a ， 0)$ 和B点 $(0 ， 10)$ 两点，且 $A B$ 与坐标轴围成的三角形的面积等于20，求a的值．

查看试题解析
18. 如图，已知AB∥DC，AE平分∠BAD，CD与AE相交于点F，∠CFE＝∠E．试说明AD∥BC．完成推理过程：
∵AB∥DC（已知）
∴∠1=∠CFE（      ）
∵AE平分∠BAD（已知）
∴∠1= ∠2 (角平分线的定义)
∵∠CFE=∠E(已知)
∴∠2=      ▲ （等量代换）
∴AD∥BC（      ）

查看试题解析
19. 在平面直角坐标系中，A、B、C三点的坐标分别为： $(- 6 ， 6)$ 、 $(- 3 ， 0)$ 、 $(0 ， 3)$ ．

(1)、画出 $△ A B C$ ，它的面积为 ▲ ；

(2)、在 $△ A B C$ 中，点C经过平移后的对应点 $C^{'} (5 ， 4)$ ，将 $△ A B C$ 作同样的平移得到 $△ A^{'} B^{'} C^{'}$ ，画出平移后的 $△ A^{'} B^{'} C^{'}$ ，并写出 $A^{'}$ 、 $B^{'}$ 的坐标；

(3)、点 $P (- 3 ， m)$ 为 $△ A B C$ 内一点，将点P向右平移4个单位后，再向下平移6个单位得到点 $Q (n ， - 3)$ ，则m= ， n= ．

查看试题解析
20. 已知 $M = \sqrt[m - 4]{m + 3}$ 是 $m + 3$ 的算术平方根， $N = \sqrt[2 m - 4 n + 3]{n - 2}$ 是 $n - 2$ 的立方根，试求：

(1)、M和N的值；

(2)、 $M + N$ 的平方根．

查看试题解析
21. 已知方程组 ${\begin{array}{l} 3 x + 2 y = k \\ 2 x + 3 y = k + 2 \end{array}$ 的解也是 $x + y = 8$ 的解．

(1)、求k的值；

(2)、这个方程组的解为．

查看试题解析
22. 已知如图：AD∥BC，E、F分别在DC、AB延长线上．∠DCB=∠DAB，AE⊥EF，∠DEA=30°．

(1)、求证：DC∥AB．

(2)、求∠AFE的大小

查看试题解析
23. 小王家购买了一套经济适用房，他家准备将地面铺上地砖，地面结构如图所示．根据图中的数据（单位：m），解答下列问题：

(1)、写出用含、的代数式表示地面总面积；

(2)、已知客厅面积比卫生间面积多21m² ，且地面总面积是卫生间面积的15倍，铺1m²地砖的平均费用为80元，求铺地砖的总费用为多少元？

查看试题解析
24. 已知如下事实：任意一个有理数与无理数的和为无理数，任意一个不为零的有理数与一个无理数的积为无理数，而零与无理数的积为零；如果 $a x + b = 0$ ，其中a，b为有理数，x为无理数，那么 $a = 0$ 且 $b = 0$ ．运用上述知识，解决下列问题：

(1)、若果 $(a - 2) \cdot \sqrt{2} + b - 3 = 0$ ，其中a，b为有理数，那么a= ， b= ；

(2)、如果 $(2 + \sqrt{2}) a - (1 - \sqrt{2}) b = 5$ ，其中a，b是有理数，求a+2b的值．

查看试题解析
25. 如图1， $C E$ 平分 $∠ A C D$ ， $A E$ 平分 $∠ B A C$ ， $∠ E A C + ∠ A C E = 90 °$

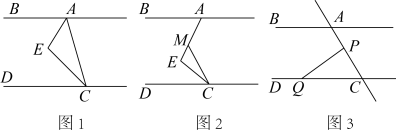(1)、请判断 $A B$ 与 $C D$ 的位置关系并说明理由；

(2)、如图2，在（1）的结论下，当 $∠ E = 90 °$ 保持不变，移动直角顶点E，使 $∠ M C E = ∠ E C D$ ，当直角顶点E点移动时，问 $∠ B A E$ 与 $∠ M C D$ 是否存在确定的数量关系？

(3)、如图3，在（1）的结论下，P为线段 $A C$ 上一定点，点Q为直线 $C D$ 上一动点，当点Q在射线 $C D$ 上运动时（点C除外）， $∠ C P Q + ∠ C Q P$ 与 $∠ B A C$ 有何数量关系？

查看试题解析
26. 如图所示，A（1，0）、点B在y轴上，将三角形OAB沿x轴负方向平移，平移后的图形为三角形DEC，且点C的坐标为（-3，2）．

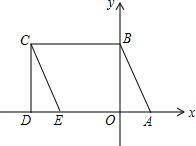(1)、直接写出点E的坐标；

(2)、在四边形ABCD中，点P从点B出发，沿“BC→CD”移动．若点P的速度为每秒1个单位长度，运动时间为t秒，回答下列问题：
①当t＝ ▲ 秒时，点P的横坐标与纵坐标互为相反数；
②求点P在运动过程中的坐标（用含t的式子表示，写出过程）；
③当3秒＜t＜5秒时，设∠CBP＝x°，∠PAD＝y°，∠BPA＝z°，试问x，y，z之间的数量关系能否确定？若能，请用含x，y的式子表示z，写出过程；若不能，说明理由．

查看试题解析