吉林省四平市2021-2022学年七年级下学期期中数学试题
试卷更新日期:2023-02-22 类型:期中考试
一、单选题
-
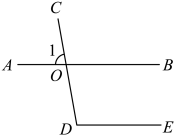
1. 3的算术平方根是( )A、9 B、-9 C、 D、2. 的相反数是( )A、0 B、 C、 D、3. 如图,直线、相交于点 , ∠1=80°,如果∥ , 那么的度数是( )
 A、80° B、90° C、100° D、110°4. 如图,下列说法错误的是( )
A、80° B、90° C、100° D、110°4. 如图,下列说法错误的是( ) A、与是同位角 B、与是内错角 C、与是对顶角 D、与是同旁内角5. 如图,∠ACB=90°,将直角三角形ABC沿着射线BC方向平移5cm,得三角形 , 已知BC=3cm,AC=4cm,AB=5cm,则阴影部分(四边形)的周长为( )
A、与是同位角 B、与是内错角 C、与是对顶角 D、与是同旁内角5. 如图,∠ACB=90°,将直角三角形ABC沿着射线BC方向平移5cm,得三角形 , 已知BC=3cm,AC=4cm,AB=5cm,则阴影部分(四边形)的周长为( ) A、16cm B、18cm C、20cm D、22cm6. 命题:①“连接直线外一点与直线上各点的所有线段中,垂线段最短.”②“内错角相等”③“在同一平面内,过一点有且只有一条直线与已知直线垂直”④“所有的实数都可以用数轴上的点表示”.其中真命题的个数为( )A、1 B、2 C、3 D、4
A、16cm B、18cm C、20cm D、22cm6. 命题:①“连接直线外一点与直线上各点的所有线段中,垂线段最短.”②“内错角相等”③“在同一平面内,过一点有且只有一条直线与已知直线垂直”④“所有的实数都可以用数轴上的点表示”.其中真命题的个数为( )A、1 B、2 C、3 D、4二、填空题
-
7. 实数-的立方根是8. 在0, , , -1.5四个实数中,最小的是 .9. 如果点P(a,5)在第一象限,那么点Q(-5,a)在第象限.10. 写出一个比大且比小的整数为 .11. 已知A、B两点的坐标分别为(2,0)、(0,1),将线段AB平移得到线段CD,点A对应点C的坐标为(4,0),则点D的坐标为 .12. 如图,直线AB与CD相交于点E,∠CEB=50°,EF⊥AE,则∠DEF的度数为 .
 13. 如图,添加一个条件能得到的是 .
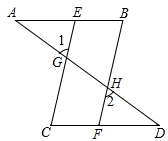
13. 如图,添加一个条件能得到的是 .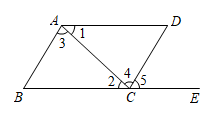 14. 如图,海关大厦与电视台大厦的大楼顶部各有一个射灯,当光柱相交时,且它们都在同一个平面内,两个大厦都垂直于地面,则∠1+∠2+∠3的度数为 .
14. 如图,海关大厦与电视台大厦的大楼顶部各有一个射灯,当光柱相交时,且它们都在同一个平面内,两个大厦都垂直于地面,则∠1+∠2+∠3的度数为 .
三、解答题
-
15. 计算: .16. 多多和爸爸、妈妈周末到白银市金鱼公园动物园游玩,回到家后,她利用平面直角坐标系画出了白银市金鱼公园动物园的景区地图,如图所示.可是她忘记了在图中标出原点、x轴和y轴,只知道东北虎的坐标为 . 请你帮她画出平面直角坐标系,并写出其他各景点的坐标.
 17. 完成推理填空.
17. 完成推理填空.如图,AB⊥BF,CD⊥BF,∠1=∠2,试说明∠3=∠E.

证明:∵AB⊥BF,CD⊥BF(已知),
∴∠ABD=∠CDF=90°(垂直定义),
∴(同位角相等,两直线平行).
∵∠1=∠2(已知),
∴ ▲ ▲ ( ),
∴( ),
∴∠3=∠E( ).
18. 已知的平方根是 , 的算术平方根是4.(1)、求a、b的值;(2)、求的平方根.19. 如图,直线AB与直线CD相交于点O,∠BOE=90°, , 求∠BOC的度数. 20. 补全下面的解答过程.
20. 补全下面的解答过程.如图, , 点E,F在直线CD下方,连接BE,DE,BF,DF,BF与CD交于点G.已知BE平分∠ABF,DE平分∠CDF, , 探究∠E与∠CDF的数量关系.

解:∵ ,
∴∠ABF= ▲ ( ),
∵BE平分∠ABF,
∴ , (角平分线的定义),
∵ ,
∴∠EBF= ▲ (等量代换),
∴( ),
∴ ▲ =∠EDF( ),
∵DE平分∠CDF,
∴∠CDF=2∠EDF(角平分线的定义)
∴ ▲ .
21. 把下列各数分别填入相应集合内:0, , 3.14, , , , .
 22. 勤俭节约是中国人民的传统美德,涛涛的爷爷是能工巧匠,他把两张破损了一部分的桌面重新拼成一张完整的正方形桌面,其面积为 , 已知他用的两张小桌面也是锯成了正方形的桌面,其中一张是边长为5dm的小板子,试问另一张较大的桌面的边长应为多少才能拼出面积为的桌面?23. 如图,在正方形网格中,每个小正方形的边长均为1个单位长度,三角形ABC的三个顶点都在网格顶点处,现将三角形ABC平移得到三角形DEF,使点A的对应点为点D,点B的对应点为点E.
22. 勤俭节约是中国人民的传统美德,涛涛的爷爷是能工巧匠,他把两张破损了一部分的桌面重新拼成一张完整的正方形桌面,其面积为 , 已知他用的两张小桌面也是锯成了正方形的桌面,其中一张是边长为5dm的小板子,试问另一张较大的桌面的边长应为多少才能拼出面积为的桌面?23. 如图,在正方形网格中,每个小正方形的边长均为1个单位长度,三角形ABC的三个顶点都在网格顶点处,现将三角形ABC平移得到三角形DEF,使点A的对应点为点D,点B的对应点为点E.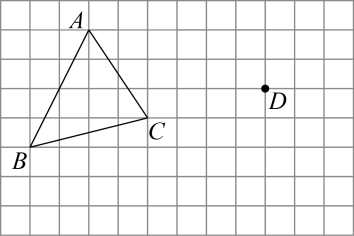 (1)、请画出平移后的三角形DEF;(2)、求三角形DEF的面积;(3)、若连接AD、CF,则这两条线段之间的关系是 .24. 在平面直角坐标系中:(1)、若点M(m-6,2m+3),点N(5,2),且MN∥x轴,求点M的坐标;(2)、若点M(a,b),点N(5,2),且MN∥y轴,MN=3,求点M的坐标.25. 某数学兴趣小组探究命题“两边分别平行的两个角相等”是否是真命题,甲同学认为该命题是真命题,并作图如图1所示,已知 , , BC与DE交于点G.
(1)、请画出平移后的三角形DEF;(2)、求三角形DEF的面积;(3)、若连接AD、CF,则这两条线段之间的关系是 .24. 在平面直角坐标系中:(1)、若点M(m-6,2m+3),点N(5,2),且MN∥x轴,求点M的坐标;(2)、若点M(a,b),点N(5,2),且MN∥y轴,MN=3,求点M的坐标.25. 某数学兴趣小组探究命题“两边分别平行的两个角相等”是否是真命题,甲同学认为该命题是真命题,并作图如图1所示,已知 , , BC与DE交于点G. (1)、根据甲同学的作图及题设,求证:∠B=∠D;(2)、乙同学对甲同学的判断提出质疑,认为该命题不一定成立,是假命题,并作图如图2所示,题设与甲同学相同,得到 , 根据乙同学的作图,试判断∠B与∠D的数量关系,并说明理由.(3)、综合甲、乙两同学的探究,两边分别平行的两个角的数量关系是: .26. 如图,有三个论断:①;②;③ , 请你从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.
(1)、根据甲同学的作图及题设,求证:∠B=∠D;(2)、乙同学对甲同学的判断提出质疑,认为该命题不一定成立,是假命题,并作图如图2所示,题设与甲同学相同,得到 , 根据乙同学的作图,试判断∠B与∠D的数量关系,并说明理由.(3)、综合甲、乙两同学的探究,两边分别平行的两个角的数量关系是: .26. 如图,有三个论断:①;②;③ , 请你从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.已知: ▲ . 结论: ▲ .
理由: