河北省唐山市路北区2021-2022学年八年级下学期期中数学试题
试卷更新日期:2023-02-22 类型:期中考试
一、单选题
-
1. 如果x是任意实数,下列各式中一定有意义的是( )A、 B、 C、 D、2. 下列式子中,属于最简二次根式的是( )A、 B、 C、 D、3. 下面计算正确的是( )A、4+=4 B、÷=3 C、·= D、=±24. 若点P(﹣1,3)在函数y=kx的图象上,则k的值为( )A、﹣3 B、3 C、 D、-5. 以下列各组数为边长能构成直角三角形的是( )A、6,8,12 B、3,4,7 C、8,15,16 D、5,12,136. 下列各曲线表示的y与x的关系中,y是x的函数的是( )A、
 B、
B、 C、
C、 D、
D、 7. 向上平移3个单位长度后能得到解析式为y=2x+1的直线表达式是( )A、y =2x+ 4 B、y =2x - 12 C、y =2x - 2 D、y =2x - 48. 设 , 用含a、b的式子表示 , 下列表示正确的是A、2a B、2b C、a+b D、ab9. 如图,在水塔O的东北方向24m处有一抽水站A,在水塔的 东南方向18m处有一建筑工地B,在AB间建一条直水管,则 水管AB的长为( )
7. 向上平移3个单位长度后能得到解析式为y=2x+1的直线表达式是( )A、y =2x+ 4 B、y =2x - 12 C、y =2x - 2 D、y =2x - 48. 设 , 用含a、b的式子表示 , 下列表示正确的是A、2a B、2b C、a+b D、ab9. 如图,在水塔O的东北方向24m处有一抽水站A,在水塔的 东南方向18m处有一建筑工地B,在AB间建一条直水管,则 水管AB的长为( ) A、40m B、45m C、30m D、35m10. 当实数的取值使得有意义时,函数中的取值范围是( )A、 B、 C、 D、11. 如图,正方形网格中的△ABC,若小方格边长为1,则△ABC的形状为( )
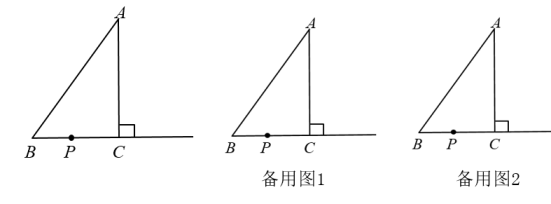
A、40m B、45m C、30m D、35m10. 当实数的取值使得有意义时,函数中的取值范围是( )A、 B、 C、 D、11. 如图,正方形网格中的△ABC,若小方格边长为1,则△ABC的形状为( )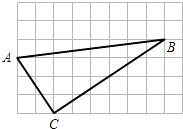 A、直角三角形 B、锐角三角形 C、钝角三角形 D、以上答案都不对12. 若y=kx+b(k>0)的图象过点(-1,0),则不等式k(x-1)+b>0的解集是( )A、x>-2 B、x>-1 C、x>0 D、x>113. 已知直线y=x+1与y=-2x+b交于点P(1,m),若y=-2x+b与x轴交于A点,B是x轴上一点,且S△PAB=4,则点B的横坐标为( )A、6 B、-2 C、6或-2 D、4或014. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )
A、直角三角形 B、锐角三角形 C、钝角三角形 D、以上答案都不对12. 若y=kx+b(k>0)的图象过点(-1,0),则不等式k(x-1)+b>0的解集是( )A、x>-2 B、x>-1 C、x>0 D、x>113. 已知直线y=x+1与y=-2x+b交于点P(1,m),若y=-2x+b与x轴交于A点,B是x轴上一点,且S△PAB=4,则点B的横坐标为( )A、6 B、-2 C、6或-2 D、4或014. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( ) A、13 B、26 C、34 D、47
A、13 B、26 C、34 D、47二、填空题
-
15. 计算:= .16. 如图,直线与轴交于点 , 则关于的方程的解为 .
 17. 函数中,y随x的增大而增大,则直线不经过第象限.18. 如图,一只蚂蚁从长为2cm,宽为2cm,高为3cm的长方形纸箱的A点沿纸箱爬到B点,那么它所行的最短路线长是cm.
17. 函数中,y随x的增大而增大,则直线不经过第象限.18. 如图,一只蚂蚁从长为2cm,宽为2cm,高为3cm的长方形纸箱的A点沿纸箱爬到B点,那么它所行的最短路线长是cm.
三、解答题
-
19. 计算(1)、(2)、20. 要画一个面积为的长方形,使它的长与宽之比为3:2,它的长、宽各应取多少?21. 已知y是x的一次函数,下表列出了部分y与x的对应值,求m的值.
x
1
0
2
y
5
m
7
22. 如图,在△ABC中,CD⊥AB于点D,AC=20,CD=12,BD=9. (1)、求BC的长;(2)、求△ABC的面积;(3)、判断△ABC的形状.23. 如图,在平面直角坐标系中,直线 过点 且与 轴交于点 ,把点 向左平移2个单位,再向上平移4个单位,得到点 .过点 且与 平行的直线交 轴于点 .
(1)、求BC的长;(2)、求△ABC的面积;(3)、判断△ABC的形状.23. 如图,在平面直角坐标系中,直线 过点 且与 轴交于点 ,把点 向左平移2个单位,再向上平移4个单位,得到点 .过点 且与 平行的直线交 轴于点 . (1)、求直线 的解析式;
(1)、求直线 的解析式;
(2)、直线 与 交于点 ,将直线 沿 方向平移,平移到经过点 的位置结束,求直线 在平移过程中与 轴交点的横坐标的取值范围.
24. 有一台风中心沿东西方向AB由点A行驶向点B,已知点C为一海港,且点C与直线AB上两点A、B的距离分别为300km和400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域. (1)、海港C会受台风影响吗?为什么?(2)、若台风的速度为20km/h,台风影响该海港持续的时间有多长?
(1)、海港C会受台风影响吗?为什么?(2)、若台风的速度为20km/h,台风影响该海港持续的时间有多长?