河北省唐山市丰润区2021-2022学年八年级下学期期中数学试卷

试卷更新日期：2023-02-22 类型：期中考试

进入出卷网下载

一、单选题

1. 若二次根式 $\sqrt{x + 2}$ 有意义，则实数x的取值范围是（）

A、x≠﹣2 B、x≥﹣2 C、x≥2 D、x≤﹣2

查看试题解析
2. 下列二次程式中，是最简二次根式的是（）

A、 $\sqrt{9}$ B、 $\sqrt{12}$ C、 $\sqrt{2}$ D、 $\sqrt{27}$

查看试题解析
3. 在▱ABCD中，如果 $∠ A = 65 °$ ，那么 $∠ C$ 的度数是（）

A、115° B、65° C、25° D、35°

查看试题解析
4. 下列长度的三条线段能组成直角三角形的是（）

A、 $4 ， 6 ， 8$ B、 $6 ， 8 ， 9$ C、 $5 ， 12 ， 13$ D、 $5 ， 11 ， 12$

查看试题解析
5. 下列各式中，运算正确的是（）

A、 $\sqrt{5} - \sqrt{3} = \sqrt{2}$ B、 $2 + \sqrt{3} = 2 \sqrt{3}$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $\sqrt{{(- 2)}^{2}} = - 2$

查看试题解析
6. 利用勾股定理，可以作出长为无理数的线段．如图，在数轴上找到点A，使OA=5，过点A作直线l垂直于OA，在1上取点B，使AB=2，以原点O为圆心，以OB长为半径作弧，弧与数轴的交点为C，那么点C表示的无理数是（）

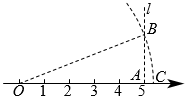A、 $\sqrt{21}$ B、 $\sqrt{29}$ C、7 D、29

查看试题解析
7. 墨迹覆盖了等式 $- 2 \sqrt{3} 〇 \sqrt{27} = \sqrt{3}$ 中的运算符号，则覆盖的运算符号是（）

A、＋ B、 $-$ C、× D、÷

查看试题解析
8. 如图，在△ABC中，CD⊥AB于点D，E，F分别为AC，BC的中点．AB＝10，BC=8，DE＝4.5，则△DEF的周长是（）

A、14.5 B、12.5 C、9.5 D、13.5

查看试题解析
9. 如图，在▱ABCD中，AE平分∠BAD，交CD边平E，AD＝3，AB＝5，则EC的长为（）

A、1 B、2 C、3 D、5

查看试题解析
10. 如图，以直角三角形的一条直角边和斜边为一边作正方形M和N，它们的面积分别为9平方厘米和25平方厘米，则直角三角形的面积为（）

A、6平方厘米 B、12平方厘米 C、24平方厘米 D、3平方厘米

查看试题解析
11. 如图，在▱ABCD中，AB⊥AC，若AB＝8，AC＝12，则BD的长是（）

A、22 B、16 C、18 D、20

查看试题解析
12. 如图，在四边形ABCD中，E，F，G，H分别是边AB，BC，CD，DA的中点．要使四边形EFGH为菱形，可以添加的一个条件是（）

A、四边形ABCD是菱形 B、AC、BD互相平分 C、
AC＝BD
D、AC⊥BD

查看试题解析

二、填空题

13. 化简 $\sqrt{18}$ 的正确结果是．

查看试题解析
14. 计算． $(\sqrt{27} - \sqrt{12}) ＋ \sqrt{3} ＝$ ．

查看试题解析
15. 如图，在Rt△ABC中，BC＝5，AB＝13，则AC＝．

查看试题解析
16. 如图，为测量位于一水塘旁的两点A，B间的距离，在地面上确定点O，分别取OA，OB的中点C，D，量得CD＝10m，则A，B之间的距离是．

查看试题解析
17. 如图，▱ABCD的对角线相交于点O，两条对角线的和为18，AD的长为5，则△OBC的周长为．

查看试题解析
18. 如图，矩形 $A B C D$ 中，对角线 $A C ， B D$ 交于点 $O$ ，如果 $∠ A D B = 30 °$ ，那么 $∠ A O B$ 的度数为．

查看试题解析
19. 如果，AD是△ABC的中线．∠ADC＝45°，BC＝4cm，把△ACD沿AD翻折，使点C落在E的位置．则BE为．

查看试题解析
20. 如图，在边长为4的正方形ABCD中，E为BC上一点，EF⊥AC于点F，EG⊥BD于点G，那么EF＋EG＝．

查看试题解析

三、解答题

21.

(1)、计算： $\sqrt{80} - \sqrt{20} ＋ \sqrt{5}$ ；

(2)、计算： $\sqrt{12} \times \frac{\sqrt{3}}{2} ＋ \sqrt{24} \div \sqrt{6}$ ．

查看试题解析
22.

(1)、计算： ${(\sqrt{3} ＋ 2)}^{2}$ ．

(2)、已知 $x = \sqrt{3} + 1 ， y = \sqrt{3} - 1$ ，求 $x^{2} - y^{2}$ 的值．

查看试题解析
23. 如图，点E、F在菱形ABCD的对角线AC上，且AF＝CE，求证：DE＝BF．

查看试题解析
24. 四边形ABCD中， $A D ∥ B C$ ， AB＝13，BC＝5，AC＝AD＝12，

(1)、求∠ACB的度数．

(2)、求CD的长，

查看试题解析
25. 如图，在▱ABCD中，对角线AC，BD相交于点O，且OA＝OD，∠OAB＝40°．求∠OAD的度数．

查看试题解析
26. 如图，在Rt△ABC中，∠ABC＝90°，D、E分别是边BC，AC的中点，连接ED并延长到点F，使DF＝ED，连接BE、BF、CF、AD．

(1)、求证：四边形BFCE是菱形；

(2)、若BC＝4，EF＝2，求AD的长．

查看试题解析