河北省石家庄市赞皇县2021-2022学年八年级下学期期中考试数学试题
试卷更新日期:2023-02-22 类型:期中考试
一、单选题
-
1. 若二次根式有意义,则x的取值范围是( )A、 B、 C、 D、2. 下列各式中,正确的是( )A、 B、 C、 D、3. 下列语句中正确的是( )A、四边都相等的四边形是矩形 B、顺次连接矩形各边中点所得的四边形是菱形 C、菱形的对角线相等 D、对角线互相垂直的平行四边形是正方形4. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、5. 如图,在中,DE平分 , , 则( )
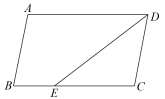 A、30° B、45° C、60° D、80°6. 如图,直线AO⊥OB,垂足为O,线段AO=3,BO=4,以点A为圆心,AB的长为半径画弧,交直线AO于点C.则OC的长为( )
A、30° B、45° C、60° D、80°6. 如图,直线AO⊥OB,垂足为O,线段AO=3,BO=4,以点A为圆心,AB的长为半径画弧,交直线AO于点C.则OC的长为( ) A、5 B、4 C、3 D、27. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间8. 已知一个直角三角形的两边长分别为3和4,则第三边长是( )A、5 B、25 C、 D、5或9. 在勾股定理的学习过程中,我们已经学会了运用以下图形,验证著名的勾股定理:这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数,图形与几何等领域中的许多数学公式和规律,它体现的数学思想是( )
A、5 B、4 C、3 D、27. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间8. 已知一个直角三角形的两边长分别为3和4,则第三边长是( )A、5 B、25 C、 D、5或9. 在勾股定理的学习过程中,我们已经学会了运用以下图形,验证著名的勾股定理:这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数,图形与几何等领域中的许多数学公式和规律,它体现的数学思想是( )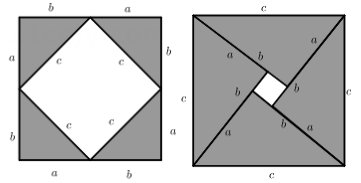 A、统计思想 B、分类思想 C、数形结合思想 D、函数思想10. 如图,矩形 中, 、 相交于点O,若 , ,则 的长为( ).
A、统计思想 B、分类思想 C、数形结合思想 D、函数思想10. 如图,矩形 中, 、 相交于点O,若 , ,则 的长为( ). A、 B、 C、 D、11. 一个四边形顺次添加下列中的三个条件便得到正方形:
A、 B、 C、 D、11. 一个四边形顺次添加下列中的三个条件便得到正方形:
a.两组对边分别相等 b.一组对边平行且相等
c.一组邻边相等 d.一个角是直角
顺次添加的条件:①a→c→d②b→d→c③a→b→c
则正确的是( )
A、仅① B、仅③ C、①② D、②③12. 如图,两根木条钉成一个角形框架 ,且 , ,将一根橡皮筋两端固定在点 , 处,拉展成线段 ,在平面内,拉动橡皮筋上的一点 ,当四边形 是菱形时,橡皮筋再次被拉长了( )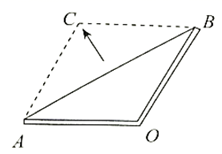 A、 B、 C、 D、13. 如图, , 、相交于P,E、F分别为、的中点,若 , 则的长是( )
A、 B、 C、 D、13. 如图, , 、相交于P,E、F分别为、的中点,若 , 则的长是( ) A、1 B、2 C、3 D、414. 如图,某自动感应门的正上方A处装着一个感应器,离地AB=2.5米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),感应门自动打开,则人头顶离感应器的距离AD等于( )
A、1 B、2 C、3 D、414. 如图,某自动感应门的正上方A处装着一个感应器,离地AB=2.5米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),感应门自动打开,则人头顶离感应器的距离AD等于( ) A、1.2米 B、1.5米 C、2.0米 D、2.5米15. 如图,在四边形ABDE中, , , 点C是边BD上一点, , , . 下列结论:①;②90°;③四边形ABDE的面积是;④;⑤该图可以验证勾股定理.其中正确的结论个数是( )
A、1.2米 B、1.5米 C、2.0米 D、2.5米15. 如图,在四边形ABDE中, , , 点C是边BD上一点, , , . 下列结论:①;②90°;③四边形ABDE的面积是;④;⑤该图可以验证勾股定理.其中正确的结论个数是( ) A、5 B、4 C、3 D、216. 如图,四边形中,AD//BC, , M是上一点,且 , 点E从点A出发以的速度向点D运动,点F从点C出发,以的速度向点B运动,当其中一点到达终点,另一点也随之停止,设运动时间为 , 则当以A、M、E、F为顶点的四边形是平行四边形时,t的值是( )
A、5 B、4 C、3 D、216. 如图,四边形中,AD//BC, , M是上一点,且 , 点E从点A出发以的速度向点D运动,点F从点C出发,以的速度向点B运动,当其中一点到达终点,另一点也随之停止,设运动时间为 , 则当以A、M、E、F为顶点的四边形是平行四边形时,t的值是( ) A、 B、3 C、3或 D、或
A、 B、3 C、3或 D、或二、填空题
-
17. 当x=时,代数式+1取最小值为 .18. 勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直的铁路经过A,B两地,则A,B间的距离为km,C到A地的距离为km.
 19. 如图,方格纸中每个小正方形的边长都是1,A、B、C、D均落在格点上.
19. 如图,方格纸中每个小正方形的边长都是1,A、B、C、D均落在格点上. (1)、;(2)、点P为BD的中点,过点P作直线 , 过点B作于点M,过点C作于点N,则矩形BCNM的面积为 .
(1)、;(2)、点P为BD的中点,过点P作直线 , 过点B作于点M,过点C作于点N,则矩形BCNM的面积为 .三、解答题
-
20. 计算:(1)、 .(2)、 .21. 先化简,再求值: , 其中 . 如图是小亮和小芳的解答过程.
 (1)、的解法是错误的,错误的原因在于未能正确地运用二次根式的性质:;(2)、先化简,再求值: , 其中;22. 如图,点E,F在 的边 , 上, , ,连接 , .求证:四边形 是平行四边形.
(1)、的解法是错误的,错误的原因在于未能正确地运用二次根式的性质:;(2)、先化简,再求值: , 其中;22. 如图,点E,F在 的边 , 上, , ,连接 , .求证:四边形 是平行四边形.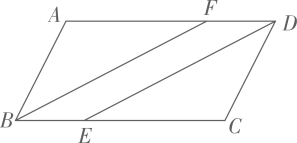 23. 如图(1)是超市的儿童玩具购物车,图(2)为某侧面简化示意图,测得支架 , , 两轮中心的距离 , 求点C到AB的距离(结果保留整数).
23. 如图(1)是超市的儿童玩具购物车,图(2)为某侧面简化示意图,测得支架 , , 两轮中心的距离 , 求点C到AB的距离(结果保留整数). 24. 如图,在中,=90°,点D在斜边AB上,E、F分别在直角边CA、BC上,且 , .
24. 如图,在中,=90°,点D在斜边AB上,E、F分别在直角边CA、BC上,且 , . (1)、求证:四边形CEDF是矩形;(2)、连接EF,若C到AB的距离是5,求EF的最小值.25. 在进行二次根式简化时,我们有时会碰上如一样的式子,其实我们还可将其进一步简化:
(1)、求证:四边形CEDF是矩形;(2)、连接EF,若C到AB的距离是5,求EF的最小值.25. 在进行二次根式简化时,我们有时会碰上如一样的式子,其实我们还可将其进一步简化:;(一)
;(二)
;(三)
以上这种化简的步骤叫做分母有理化
还可以用以下方法化简:
;(四)
(1)、化简==(2)、请用不同的方法化简 . (要求写出必要步骤)①参照(三)式得=
②参照(四)式得=
(3)、化简:26. 已知在菱形ABCD中,点P在CD上,连接AP. (1)、在BC上取点Q,使得∠PAQ=∠B,
(1)、在BC上取点Q,使得∠PAQ=∠B,①如图1,当AP⊥CD于点P时,线段AP与AQ之间的数量关系是 ▲ .
②如图2,当AP与CD不垂直时,判断①中的结论是否仍然成立,若成立,请给出证明,若不成立,则需说明理由.
(2)、在CD的延长线取点N,使得∠PAN=∠B,①根据描述在图3中补全图形.
②若AB=4,∠B=60°,∠ANC=45°,求此时线段DN的长.