河北省衡水市景县九校联考2021-2022学年八年级下学期期中考试数学试题
试卷更新日期:2023-02-22 类型:期中考试
一、单选题
-
1. 已知式子有意义,则的值可以是( )A、3 B、2 C、1 D、-12. 在中, , , 的对应边长分别为 , , , 若 , , 满足 , 则( )A、 B、 C、 D、无法确定3. 若 , 则横线处应为( )A、 B、 C、 D、4. 平行四边形的对角线与交于点 , 若 , , 则( )A、5 B、6 C、10 D、115. 已知直角三角形的一条直角边长为 , 斜边长为 , 则另一条直角边的长为( )A、8 B、 C、 D、6. 如图,在平行四边形中, , 则的度数为( )
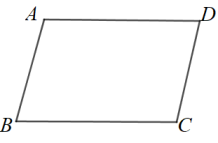 A、 B、 C、 D、7. 若 , , 则的值为( )A、 B、 C、 D、8. 下列命题的逆命题是真命题的是( )A、对顶角相等 B、正方形的四个角均为直角 C、矩形的对角线相等 D、菱形的四条边都相等9. 如图,甲,乙,丙三人手中各有一张纸质卡片,卡片的正面分别写有一个算式,则这三张卡片中,算式的计算结果是有理数的有( )
A、 B、 C、 D、7. 若 , , 则的值为( )A、 B、 C、 D、8. 下列命题的逆命题是真命题的是( )A、对顶角相等 B、正方形的四个角均为直角 C、矩形的对角线相等 D、菱形的四条边都相等9. 如图,甲,乙,丙三人手中各有一张纸质卡片,卡片的正面分别写有一个算式,则这三张卡片中,算式的计算结果是有理数的有( ) A、0张 B、1张 C、2张 D、3张10. 如图,矩形的对角线与交于点 , 若 , 则的度数为( )
A、0张 B、1张 C、2张 D、3张10. 如图,矩形的对角线与交于点 , 若 , 则的度数为( ) A、 B、 C、 D、11. 如图,在四边形ABCD中,对角线AC,BD交于点O,且OA=OC,添加下列条件后,仍无法判定四边形ABCD是平行四边形的是( )
A、 B、 C、 D、11. 如图,在四边形ABCD中,对角线AC,BD交于点O,且OA=OC,添加下列条件后,仍无法判定四边形ABCD是平行四边形的是( ) A、AB=CD B、AD∥BC C、OB=OD D、AB∥CD12. 如图,在中, , , , 和的平分线交于点 , 则的度数为( )
A、AB=CD B、AD∥BC C、OB=OD D、AB∥CD12. 如图,在中, , , , 和的平分线交于点 , 则的度数为( ) A、 B、 C、 D、13. 如图,在中,是的中位线,是边的中点,连接 . 若 , , 则四边形的周长为( )
A、 B、 C、 D、13. 如图,在中,是的中位线,是边的中点,连接 . 若 , , 则四边形的周长为( ) A、8 B、10 C、12 D、1414. 如图,在平行四边形中,小明利用尺规作直线 , 步骤如下:①分别以点 , 为圆心,以大于长为半径画弧;②两弧分别交于点 , , 作直线;③直线分别交 , 于点 , , 与交于点 , 连接 , . 若 , 则四边形的周长为( )
A、8 B、10 C、12 D、1414. 如图,在平行四边形中,小明利用尺规作直线 , 步骤如下:①分别以点 , 为圆心,以大于长为半径画弧;②两弧分别交于点 , , 作直线;③直线分别交 , 于点 , , 与交于点 , 连接 , . 若 , 则四边形的周长为( ) A、32 B、40 C、48 D、5615. 如图,已知树(垂直于地面)上的点处(米)有两只松鼠,为抢到处(点 , 在同一水平地面上,米)的坚果,一只松鼠沿到达点处,另一只松鼠沿到达点处.若两只松鼠经过的路程相等,则树的高为( )
A、32 B、40 C、48 D、5615. 如图,已知树(垂直于地面)上的点处(米)有两只松鼠,为抢到处(点 , 在同一水平地面上,米)的坚果,一只松鼠沿到达点处,另一只松鼠沿到达点处.若两只松鼠经过的路程相等,则树的高为( ) A、6.5米 B、7.0米 C、7.5米 D、8米16. 图中的两个图形都是由边长为1的小正方形拼成的,甲、乙两名同学将它们分别沿着两条垂直的虚线(乙: , 分别是小正方形一边上的中点)剪开,准备拼一个与原来面积相等的正方形,则( )
A、6.5米 B、7.0米 C、7.5米 D、8米16. 图中的两个图形都是由边长为1的小正方形拼成的,甲、乙两名同学将它们分别沿着两条垂直的虚线(乙: , 分别是小正方形一边上的中点)剪开,准备拼一个与原来面积相等的正方形,则( )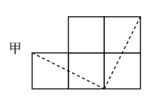
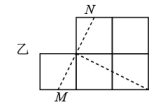 A、甲、乙都可以 B、甲、乙都不可以 C、甲不可以、乙可以 D、甲可以、乙不可以
A、甲、乙都可以 B、甲、乙都不可以 C、甲不可以、乙可以 D、甲可以、乙不可以二、填空题
-
17. 如图,已知在中, , .
 (1)、的度数为;(2)、若是的中点,则的度数为 .18. 如图,已知正方形的边在数轴上,点表示的数为-1,点表示的数为1,点 , 在数轴上方.
(1)、的度数为;(2)、若是的中点,则的度数为 .18. 如图,已知正方形的边在数轴上,点表示的数为-1,点表示的数为1,点 , 在数轴上方.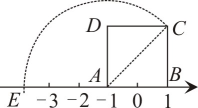 (1)、的长为;(2)、以点为圆心,长为半径画弧,交数轴负方向于点 , 则点表示的数为 .19. 如图,在矩形中, , , 是边上一点,将矩形沿向上翻折,点落在点处,点落在点处,与交于点 , 设的长为 .
(1)、的长为;(2)、以点为圆心,长为半径画弧,交数轴负方向于点 , 则点表示的数为 .19. 如图,在矩形中, , , 是边上一点,将矩形沿向上翻折,点落在点处,点落在点处,与交于点 , 设的长为 .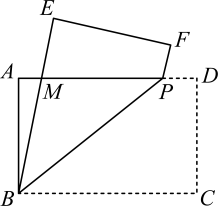 (1)、当点与点A重合时,DP的长为;(2)、当时,m的取值范围是 .
(1)、当点与点A重合时,DP的长为;(2)、当时,m的取值范围是 .三、解答题
-
20. 计算下列各小题:(1)、;(2)、 .21. 如图,已知是的中线,于点 , , , .
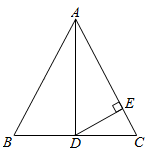 (1)、求的长;(2)、求证:垂直平分线段 .22. 已知图1是超市购物车,图2是超市购物车侧面示意图,测得支架 , , , 均与地面平行.
(1)、求的长;(2)、求证:垂直平分线段 .22. 已知图1是超市购物车,图2是超市购物车侧面示意图,测得支架 , , , 均与地面平行. (1)、若支架与之间的夹角()为 , 求两轮轮轴 , 之间的距离;(2)、若的长度为 , , 求扶手到所在直线的距离.23. 如图,已知在菱形中,对角线与交于点 , 延长到点 , 使 , 延长到点 , 使 , 顺次连接点 , , , , 且 , .
(1)、若支架与之间的夹角()为 , 求两轮轮轴 , 之间的距离;(2)、若的长度为 , , 求扶手到所在直线的距离.23. 如图,已知在菱形中,对角线与交于点 , 延长到点 , 使 , 延长到点 , 使 , 顺次连接点 , , , , 且 , . (1)、求菱形的面积;(2)、求证:四边形是矩形;(3)、四边形的周长为 .24. 如图,已知四边形和均是正方形,点K在上,延长到点H,使 , 连接 .
(1)、求菱形的面积;(2)、求证:四边形是矩形;(3)、四边形的周长为 .24. 如图,已知四边形和均是正方形,点K在上,延长到点H,使 , 连接 . (1)、求证:;(2)、求证:四边形是正方形;(3)、若四边形的面积为10, , 求点之间的距离.25. 根据学习“数与式”积累的经验,探究下面二次根式的运算规律.(1)、【探究】将题目中的横线处补充完整;
(1)、求证:;(2)、求证:四边形是正方形;(3)、若四边形的面积为10, , 求点之间的距离.25. 根据学习“数与式”积累的经验,探究下面二次根式的运算规律.(1)、【探究】将题目中的横线处补充完整;①;
②;
③;
④;
…
(2)、【归纳】若为正整数,用含的代数式表示上述运算规律,并加以证明;(3)、【应用】计算:;(4)、小明写出一个等式( , 均为正整数),若该等式符合上述规律,则的值为 .26. 如图,在平行四边形ABCD中,AB=6cm,AD=10cm,点P在边AD上,以每秒1cm的速度从点A向点D运动,点Q在边CB上,以每秒2cm的速度从点C出发,在CB之间做往返运动.两个动点同时出发,当点P到达点D时两点同时停止运动.设运动时间为t秒(t>0).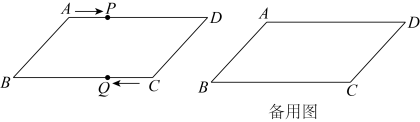 (1)、用含t的代数式表示线段AP及BQ的长度;(2)、在点P,Q的运动过程中,t为何值时,四边形APQB为平行四边形?(3)、在点P,Q的运动过程中,是否存在t的值,使四边形APQB为菱形?若存在,直接写出t的值;若不存在,请说明理由.
(1)、用含t的代数式表示线段AP及BQ的长度;(2)、在点P,Q的运动过程中,t为何值时,四边形APQB为平行四边形?(3)、在点P,Q的运动过程中,是否存在t的值,使四边形APQB为菱形?若存在,直接写出t的值;若不存在,请说明理由.