河北省沧州市孟村回族自治县2021-2022学年八年级下学期期中数学试题
试卷更新日期:2023-02-22 类型:期中考试
一、单选题
-
1. 下列各数中,与 的积为有理数的是( )A、 B、 C、 D、2. 将 化简,正确的结果是( )A、 B、 C、 D、3. 选择下列计算正确的答案是( )A、 B、 C、 D、4. 设直角三角形的两条直角边长分别为a和b,斜边长为c.已知b=8,c=10,则a的值为( )A、2 B、6 C、5 D、365. 如图,在平面直角坐标系中,点P坐标为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
 A、-4和-3之间 B、3和4之间 C、-5和-4之间 D、4和5之间6. 如图是台阶的示意图,已知每级台阶的宽度都是30 cm,每级台阶的高度都是15 cm,连接AB,则AB等于( )
A、-4和-3之间 B、3和4之间 C、-5和-4之间 D、4和5之间6. 如图是台阶的示意图,已知每级台阶的宽度都是30 cm,每级台阶的高度都是15 cm,连接AB,则AB等于( )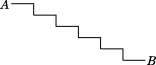 A、195 cm B、200 cm C、205 cm D、210 cm7. 如图,在平行四边形 中, ,点 , 分别是 , 的中点,则 等于( )
A、195 cm B、200 cm C、205 cm D、210 cm7. 如图,在平行四边形 中, ,点 , 分别是 , 的中点,则 等于( ) A、2 B、3 C、4 D、68. 已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是( )
A、2 B、3 C、4 D、68. 已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是( )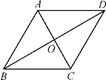 A、16 B、16 C、8 D、89. 如图,过矩形ABCD的四个顶点作对角线AC、BD的平行线,分别相交于E、F、G、H四点,则四边形EFGH为( )
A、16 B、16 C、8 D、89. 如图,过矩形ABCD的四个顶点作对角线AC、BD的平行线,分别相交于E、F、G、H四点,则四边形EFGH为( )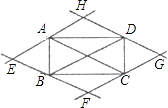 A、平行四边形 B、矩形 C、菱形 D、正方形10. 如图,将△ABC放在正方形网格图中(图中每个小正方形的边长均为1),点A,B,C恰好在网格图中的格点上,那么△ABC中BC边上的高是( )
A、平行四边形 B、矩形 C、菱形 D、正方形10. 如图,将△ABC放在正方形网格图中(图中每个小正方形的边长均为1),点A,B,C恰好在网格图中的格点上,那么△ABC中BC边上的高是( ) A、 B、 C、 D、11. ①
A、 B、 C、 D、11. ①②
③
④
以上推导中的错误在第几步( )
A、① B、② C、③ D、④12. 如果1≤a≤ ,则 +|a-2|的值是( )A、6+a B、﹣6﹣a C、﹣a D、113. 如图,在平行四边形中, , , 对角线 , 相交于点 , 则的取值范围是( ) A、 B、 C、 D、14. 如图,在平行四边形ABCD中,过对角线BD上一点P作EF∥AB,GH∥AD,与各边交点分别为点E,F,G,H,则图中面积相等的平行四边形的对数为( )
A、 B、 C、 D、14. 如图,在平行四边形ABCD中,过对角线BD上一点P作EF∥AB,GH∥AD,与各边交点分别为点E,F,G,H,则图中面积相等的平行四边形的对数为( ) A、3对 B、4对 C、5对 D、6对15. 图1中,每个小正方形的边长为1, 的三边a,b,c的大小关系是( )
A、3对 B、4对 C、5对 D、6对15. 图1中,每个小正方形的边长为1, 的三边a,b,c的大小关系是( ) A、a<c<b B、a<b<c C、c<a<b D、c<b<a16. 有一个边长为的正方形,经过一次“生长”后在它的上侧生长出两个小正方形(如图),且三个正方形所围成的三角形是直角三角形;再经过一次“生长”后变成了图 , 如此继续“生长”下去,则“生长”第k次后所有正方形的面积和为( ).
A、a<c<b B、a<b<c C、c<a<b D、c<b<a16. 有一个边长为的正方形,经过一次“生长”后在它的上侧生长出两个小正方形(如图),且三个正方形所围成的三角形是直角三角形;再经过一次“生长”后变成了图 , 如此继续“生长”下去,则“生长”第k次后所有正方形的面积和为( ).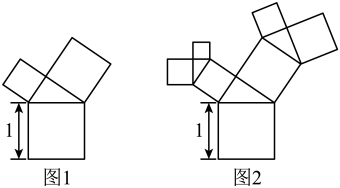 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
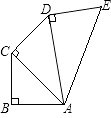
17. 计算 的结果是 .18. 如图所示,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则AE= .
 19. 如图,在边长为的菱形中, , 连接对角线 , 以为边作第二个菱形 , 使 , 连接 , 再以为边作第三个菱形 , 使…则的长度是;按此规律所作的第个菱形的边长是 .
19. 如图,在边长为的菱形中, , 连接对角线 , 以为边作第二个菱形 , 使 , 连接 , 再以为边作第三个菱形 , 使…则的长度是;按此规律所作的第个菱形的边长是 .
三、解答题
-
20. 若最简二次根式 和 是同类二次根式.(1)、求x、y的值;(2)、求 的值.21. 如图,一只蚂蚁从点A沿数轴向右直爬2个单位长度到达点B,点A表示-
 , 设点B所表示的数为m.
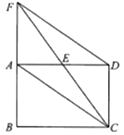
, 设点B所表示的数为m. (1)、求m的值;(2)、求|m-1|+(m+)2的值.22. 如图,正方形 中, 是 上的一点,连接 ,过 点作 ,垂足为点 ,延长 交 于点 ,连接 .
(1)、求m的值;(2)、求|m-1|+(m+)2的值.22. 如图,正方形 中, 是 上的一点,连接 ,过 点作 ,垂足为点 ,延长 交 于点 ,连接 .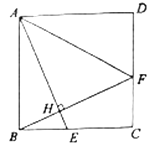 (1)、求证: .
(1)、求证: .
(2)、若正方形边长是5, ,求 的长.23. 如图,在 中, ,且周长为 ,点 从点 开始沿 边向 点以每秒 的速度移动;点 从点 开始沿 边向点 以每秒 的速度移动,如果 , 同时出发,问过 时, 的面积为多少? 24. 中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC 中,∠ACB=90°,若 AC=b,BC=a,请你利用这个图形解决下列问题:
24. 中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC 中,∠ACB=90°,若 AC=b,BC=a,请你利用这个图形解决下列问题: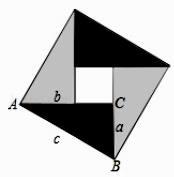 (1)、试说明 a2+b2=c2;(2)、如果大正方形的面积是 10,小正方形的面积是2,求(a+b)2的值.
(1)、试说明 a2+b2=c2;(2)、如果大正方形的面积是 10,小正方形的面积是2,求(a+b)2的值.