河北省沧州市东光县2021-2022学年八年级下学期期中数学试题
试卷更新日期:2023-02-22 类型:期中考试
一、单选题
-
1. 要使二次根式有意义,实数x的取值范围是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 下列各组数中,是勾股数的是( )A、9,16,25 B、2,2, C、1, , D、9,40,414. 如图,在四边形中, , 添加下列一个条件后,一定能判定四边形是平行四边形的是( )
 A、 B、 C、 D、5. 三边分别为 , , , 在下列条件中,不能判定是直角三角形的是( )A、 B、 C、 D、两内角互余6. 下列说法正确的是( )A、对角线相等的四边形是平行四边形 B、有一个角为直角的四边形是矩形 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直且相等的平行四边形是正方形7. 已知直线 , , 互相平行,直线 与 的距离是 ,直线 与 的距离是 ,那么直线 与 的距离是( )A、 或 B、 C、 D、8. 若 , 则代数式的值为( )A、2005 B、-2003 C、2022 D、-20209. 如图是一株美丽的“勾股树”,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形 , , , 的面积分别为5,9,3,5,则最大的正方形的面积是( )
A、 B、 C、 D、5. 三边分别为 , , , 在下列条件中,不能判定是直角三角形的是( )A、 B、 C、 D、两内角互余6. 下列说法正确的是( )A、对角线相等的四边形是平行四边形 B、有一个角为直角的四边形是矩形 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直且相等的平行四边形是正方形7. 已知直线 , , 互相平行,直线 与 的距离是 ,直线 与 的距离是 ,那么直线 与 的距离是( )A、 或 B、 C、 D、8. 若 , 则代数式的值为( )A、2005 B、-2003 C、2022 D、-20209. 如图是一株美丽的“勾股树”,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形 , , , 的面积分别为5,9,3,5,则最大的正方形的面积是( )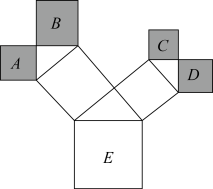 A、19 B、22 C、 D、2610. 如图所示,在矩形中,已知于 , , , 则的长为( )
A、19 B、22 C、 D、2610. 如图所示,在矩形中,已知于 , , , 则的长为( ) A、 B、 C、 D、11. 如图,在一个长方形中无重叠的放入面积分别为和的两张正方形纸片,则图中空白部分的面积为( )
A、 B、 C、 D、11. 如图,在一个长方形中无重叠的放入面积分别为和的两张正方形纸片,则图中空白部分的面积为( )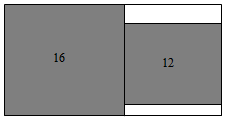 A、 B、 C、 D、12. 如图,四边形是菱形,点、分别在边、上,且 , . 若 , 则的度数为( )
A、 B、 C、 D、12. 如图,四边形是菱形,点、分别在边、上,且 , . 若 , 则的度数为( ) A、 B、 C、 D、13. 如图,在中, , 点、分别是、的中点,连接、 , 过作交的延长线于点 . 若四边形的周长是 , 的长为 , 则的周长是( )
A、 B、 C、 D、13. 如图,在中, , 点、分别是、的中点,连接、 , 过作交的延长线于点 . 若四边形的周长是 , 的长为 , 则的周长是( ) A、 B、 C、 D、14. 如图所示,点是正方形的对角线上一点, , , 垂足分别是、 . 若 , , 则的长是( )
A、 B、 C、 D、14. 如图所示,点是正方形的对角线上一点, , , 垂足分别是、 . 若 , , 则的长是( ) A、14 B、10 C、8 D、615. 新冠疫情防控过程中,某中学在大门口的正上方A处装着一个红外线激光测温仪,离地米(如图所示),当人体进入感应范围内时,测温仪就会显示人体体温.一个身高1.6米的学生(米)正对门缓慢走到离门1.2米的地方时(米),测温仪自动显示体温,则人头顶离测温仪的距离等于( )
A、14 B、10 C、8 D、615. 新冠疫情防控过程中,某中学在大门口的正上方A处装着一个红外线激光测温仪,离地米(如图所示),当人体进入感应范围内时,测温仪就会显示人体体温.一个身高1.6米的学生(米)正对门缓慢走到离门1.2米的地方时(米),测温仪自动显示体温,则人头顶离测温仪的距离等于( ) A、1.2米 B、1.3米 C、1.4米 D、1.5米16. 如图,在平行四边形 中, ,以点A为圆心, 为半径画弧与 交于点F,然后以大于 为半径,分别以B,F为圆心画弧交于点G,连接 交 于点E,若 , ,则 的长为( )
A、1.2米 B、1.3米 C、1.4米 D、1.5米16. 如图,在平行四边形 中, ,以点A为圆心, 为半径画弧与 交于点F,然后以大于 为半径,分别以B,F为圆心画弧交于点G,连接 交 于点E,若 , ,则 的长为( )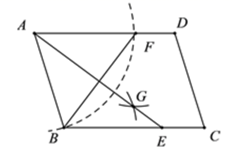 A、 B、 C、5 D、10
A、 B、 C、5 D、10二、填空题
-
17. 计算的结果是 . 已知最简二次根式与能进行合并,则 .18. 如图,在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过到达与高台A水平距离为17米,高为3米的矮台 ,
 (1)、旗杆的高度米;(2)、玛丽在荡绳索过程中离地面的最低点的高度米.
(1)、旗杆的高度米;(2)、玛丽在荡绳索过程中离地面的最低点的高度米.三、解答题
-
19. 如图,在中,是中点,平分 , ,
 (1)、与的位置关系是;(2)、若 , , 则 .20. 计算:(1)、;(2)、 .21. 如图,在正方形网格中,每个小正方形的边长都是1,四边形的顶点都在格线的交点上.解答下列问题:
(1)、与的位置关系是;(2)、若 , , 则 .20. 计算:(1)、;(2)、 .21. 如图,在正方形网格中,每个小正方形的边长都是1,四边形的顶点都在格线的交点上.解答下列问题: (1)、求四边形的面积;(2)、连接 , 请判断和是什么特殊形状的三角形,并说明理由.22. 如图,、分别是的两条高,点、点分别是、的中点.
(1)、求四边形的面积;(2)、连接 , 请判断和是什么特殊形状的三角形,并说明理由.22. 如图,、分别是的两条高,点、点分别是、的中点. (1)、求证:;(2)、若 , , 求 .23. 如图,点 , , , 在同一条直线上, , 过点 , 分别作 , , 连接、、 , . 求证:与互相平分.
(1)、求证:;(2)、若 , , 求 .23. 如图,点 , , , 在同一条直线上, , 过点 , 分别作 , , 连接、、 , . 求证:与互相平分. 24. 如图,在中, , , . 点从点出发沿方向以的速度向终点运动,点从点出发沿方向以的速度向终点运动, , 两点同时出发,设点的运动时间为秒.
24. 如图,在中, , , . 点从点出发沿方向以的速度向终点运动,点从点出发沿方向以的速度向终点运动, , 两点同时出发,设点的运动时间为秒. (1)、求的长;(2)、当时,求、两点之间的距离;(3)、当时,求的值.
(1)、求的长;(2)、当时,求、两点之间的距离;(3)、当时,求的值.

