河北省保定市易县2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-02-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列二次根式中，最简二次根式是（）

A、 $\sqrt{5}$ B、 $\sqrt{12}$ C、 $\sqrt{\frac{1}{7}}$ D、 $\sqrt{m^{2}}$

查看试题解析
2. 下列各式中，从左向右变形正确的是（）

A、 $\sqrt{4} = \pm 2$ B、 $\sqrt{{(- 3)}^{2}} = 3$ C、 $\sqrt{6} = \sqrt{- 2} \times \sqrt{3}$ D、 $\sqrt{8} + \sqrt{2} = \sqrt{10}$

查看试题解析
3. 下列四组线段中，可以构成直角三角形的是（）

A、1，1，1 B、2，3，4 C、1，2，3 D、5，12，13

查看试题解析
4. 下列图形中是中心对称图形的是（）

A、等边三角形 B、等腰三角形 C、平行四边形 D、正五边形

查看试题解析
5. 在矩形ABCD中，对角线AC，BD交于点O，且∠AOD＝120°．若AB＝3，则BC的长为（）

A、 $\sqrt{3}$ B、3 C、 $3 \sqrt{3}$ D、6

查看试题解析
6. 下列各命题都成立，逆命题也成立的有（）
⑴同旁内角互补，两直线平行⑵全等三角形的对应边相等
⑶如果两个角是直角，那么它们相等⑷如果两个实数相等，那么它们的平方相等

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图，在平面直角坐标系 $x O y$ 中，菱形 $O A B C$ 的顶点 $C$ 在 $x$ 轴的正半轴上．若点 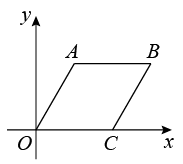$A$ 的坐标是 $(3 ， 4)$ ，则点 $B$ 的坐标为（）

A、 $(5 ， 4)$ B、 $(5 ， 3)$ C、 $(8 ， 3)$ D、 $(8 ， 4)$

查看试题解析
8. 如图，四边形ABCD的对角线相交于点O ，且互相平分．若添加下列条件，不能判定四边形ABCD为矩形的是（）

A、AC＝BD B、∠DAB＝90° C、AB＝AD D、∠ADC+∠ABC＝180°

查看试题解析
9. 如图，平行四边形ABCD的对角线AC和BD相交于点O，过点O的直线分别交AD和BC于点F，E，若设该平行四边形的面积为2，则图中阴影部分的面积为（）

A、4 B、1 C、 $\frac{1}{2}$ D、无法确定

查看试题解析
10. 如图，在 $▱ A B C D$ 中，AE平分∠BAD，交CD边于E，AD＝6，EC＝4，则AB的长为（）

A、1 B、6 C、10 D、12

查看试题解析
11. 如图，正方形ABCD的面积为8，菱形AECF的面积为4，则EF的长是（）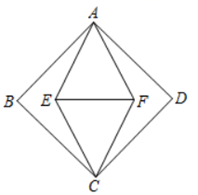

A、4 B、 $\sqrt{5}$ C、2 D、1

查看试题解析
12. 在Rt△ABC中，∠ACB＝90°，AC＝BC＝1.点Q在直线BC上，且AQ＝2，则线段BQ的长为（）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、 $\sqrt{3} + 1$ 或 $\sqrt{3} - 1$ D、 $\sqrt{5} + 1$ 或 $\sqrt{5} - 1$

查看试题解析
13. 在平面直角坐标系xOy中，如图，四边形ABCD是菱形，∠DAB＝60°，点P是边CD的中点，如果菱形的周长为16，那么点P的坐标是（）

A、（4，4） B、（2，2） C、（ $2 \sqrt{3}$ ，1） D、（ $\sqrt{3}$ ，1）

查看试题解析
14. 如图，在四边形ABCD中，AB∥CD，对角线AC，BD相交于点O．添加下列条件中的一个，若可推出该四边形是平行四边形．则添加的条件可以是（）
①AD∥BC，②AB＝CD，③AD＝BC，④∠ADC＝∠ABC，⑤BO＝DO，⑥∠DBA＝∠CAB．

A、①②③⑤ B、①②④⑤ C、①②④⑥ D、①③④⑥

查看试题解析
15. 满足下列条件的四边形是正方形的有（）
①对角线互相垂直且相等的平行四边形 ②对角线互相垂直的矩形③对角线相等的菱形 ④对角线互相垂直平分且相等的四边形

A、①③④ B、①②④ C、②③④ D、①②③④

查看试题解析
16. 如图，等腰△ABC中，点P是底边BC上的动点（不与点B，C重合），过点P分别作AB、AC的平行线PM、PN，交AC、AB于点M、N，则下列数量关系一定正确的是（）

A、PM+PN＝AB B、PM+PN＝BC C、PM+PN＝2BC D、PM+PN＝AB+BC

查看试题解析

二、填空题

17. 已知 $\sqrt{2} \approx 1.414$ ，则 $\sqrt{\frac{1}{2}} \approx$ ； $\sqrt{8} \approx$ .

查看试题解析
18. 如图，菱形ABCD中， $A B = 10$ ， AC，BD交于点O，若E是边AD的中点，∠AEO＝ $32 °$ ，则OE的长等于， ∠ADO的度数为.

查看试题解析
19. 图1中菱形的两条对角线长分别为6和8，将其沿对角线裁分为四个三角形，将这四个三角形无重叠地拼成如图2所示的图形，则图1中菱形的面积等于；图2中间的小四边形的面积等于．

查看试题解析

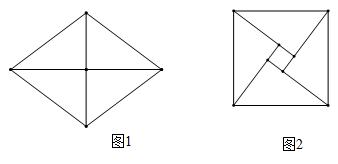
三、解答题

20. 已知 $x$ = $\sqrt{5} - 1$ ，求代数式 $x^{2} + 5 x - 6$ 的值.

查看试题解析
21. 如图，在▱ABCD中，DE⊥AB ， BF⊥CD ，垂足分别为E ， F ．求证：BE＝DF ．

查看试题解析
22. 做一个底面积为 $24 c m^{2}$ ，长、宽、高的比为4：2：1的长方体；求：

(1)、这个长方体的长、宽、高分别是多少？

(2)、长方体的表面积是多少？

(3)、长方体的体积是多少？

查看试题解析
23. 如图，在 $▱$ ABCD中，BD＝AD，延长CB到点E，使BE＝BD，连接AE.

(1)、求证：四边形AEBD是菱形；

(2)、连接DE交AB于点F，若 $D C = \sqrt{10}$ ， $D C ： D E = 1 ： 3$ ，求AD的长.

查看试题解析
24. 下面是小明设计的“作矩形ABCD”的尺规作图过程：已知：在Rt△ABC中，∠ABC=90°.求作：矩形ABCD．
作法：如图
①以点B为圆心，AC长为半径作弧；
②以点C为圆心，AB长为半径作弧；
③两弧交于点D，A，D在BC同侧；
④连接AD，CD．
所以四边形ABCD是矩形，
根据小明设计的尺规作图过程，

(1)、使用直尺和圆规，补全图形；(保留作图痕迹)

(2)、完成下面的证明.
证明：链接BD．
∵AB= ▲ ， AC= ▲ ， BC=BC
∴ΔABC≌ΔDCB
∴∠ABC=∠DCB=90°
∴AB∥CD．
∴四边形ABCD是平行四边形
∵∠ABC=90°
∴四边形ABCD是矩形.（）(填推理的依据)

查看试题解析
25. 如图，在 $▱$ ABCD中，对角线AC，BD交于点O，过点B作BE⊥CD于点E，延长CD到点F，使DF=CE，连接AF.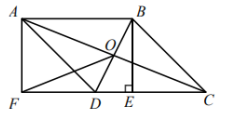

(1)、求证：四边形ABEF是矩形；

(2)、连接OF，若AB=6，DE=2，∠ADF=45°，求OF的长度.

查看试题解析
26. 在矩形ABCD中，AB=3，AD=2，点E是射线DA上一点，连接EB，以点E为圆心EB长为半径画弧，交射线CB于点F，作射线FE与CD延长线交于点G．

(1)、如图1，若DE=5，则∠DEG=°；

(2)、若∠BEF=60°，请在图2中补全图形，并求EG的长；

(3)、若以E，F，B，D为顶点的四边形是平行四边形，此时EG的长为．

查看试题解析