河北省保定市定州市2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-02-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列二次根式中属于最简二次根式的是(　 )

A、 $\sqrt{5}$ B、 $\sqrt{8}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\sqrt{0.3}$

查看试题解析
2. 若式子 $\sqrt{x + 1}$ 在实数范围内有意义，则 $x$ 的取值范围是（）

A、 $x \neq - 1$ B、 $x ≥ 1$ C、 $x \geq - 1$ D、 $x < - 1$

查看试题解析
3. 在矩形 $A B C D$ 中， $A C$ 、 $B D$ 相交于点 $O$ ，若 $A O = 3$ ，则 $B D$ 的长为（）．

A、4 B、6 C、8 D、10

查看试题解析
4. 下列各式，计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $3 \sqrt{3} - \sqrt{3} = 3$ C、 $2 \sqrt{5} \times 3 \sqrt{5} = 6 \sqrt{5}$ D、 $(\sqrt{8} - \sqrt{6}) \div \sqrt{2} = 2 - \sqrt{3}$

查看试题解析
5. 在以下列线段a、b、c的长为三边的三角形中，不能构成直角三角形的是（）

A、a＝9，b＝41，c＝40 B、a＝5，b＝5，c＝ $5 \sqrt{2}$ C、a：b：c＝3：4：5 D、a＝11，b＝12，c＝15

查看试题解析
6. 如图，两张对边平行且等宽的纸条交叉叠放在一起，重合部分构成的四边形ABCD是（）

A、平行四边形 B、菱形 C、矩形 D、正方形

查看试题解析
7. 如图， $▱ A B C D$ 中，对角线 $A C$ 与 $B D$ 交于点O， $∠ D A C = 42 °$ ， $∠ C B D = 23 °$ ，则 $∠ C O D$ 是（）

A、63° B、65° C、67° D、69°

查看试题解析
8. 下列判断错误的是（）

A、对角线相等的四边形是矩形 B、对角线相互垂直平分的四边形是菱形 C、对角线相互垂直且相等的平行四边形是正方形 D、对角线相互平分的四边形是平行四边形

查看试题解析
9. 如图，E是平行四边形内任一点，若S_{平行四边形ABCD}＝8，则图中阴影部分的面积是（）

A、3 B、4 C、5 D、6

查看试题解析
10. 如图，数轴上点A、B分别对应1、2，过点B作PQ⊥AB，以B为圆心，AB长为半径画弧，交PQ于点C，以原点O为圆心，OC长为半径画弧，交数轴于点M，则点M对应的数是（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $\sqrt{6}$ D、 $\sqrt{5}$

查看试题解析
11. 如图，在Rt△ABC中，∠ACB=90°，点D是AB的中点，且CD= $\frac{\sqrt{5}}{2}$ ，如果Rt△ABC的面积为1，则它的周长为（　　）

A、 $\frac{\sqrt{5} + 1}{2}$ B、 $\sqrt{5}$ +1 C、 $\sqrt{5}$ +2 D、 $\sqrt{5}$ +3

查看试题解析
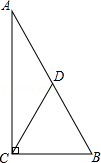12. 如图，正方形ABCD的边长为4，点E在对角线BD上，且 $∠ B A E ＝ 22 . 5°$ ， EF⊥AB，垂足为F，则EF的长为（）

A、1 B、 $\sqrt{2}$ C、 $4 - 2 \sqrt{2}$ D、 $3 \sqrt{2} - 4$

查看试题解析

二、填空题

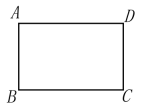
13. 若一个多边形的内角和为1800°，则这个多边形是．（填形状）

查看试题解析
14. 如图，在四边形 $A B C D$ 中， $A D / / B C$ ， $∠ D = 90 °$ ，若再添加一个条件，就能推出四边形 $A B C D$ 是矩形，你所添加的条件是．（写出一种情况即可）．

查看试题解析
15. 如图，四边形 $A B C D$ 为菱形，四边形 $A O B E$ 为矩形， $O$ ， $C$ ， $D$ 三点的坐标为 $(0 ， 0)$ ， $(2 ， 0)$ ， $(0 ， 1)$ ，则点 $E$ 的坐标为.

查看试题解析
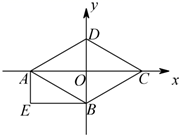16. 直角三角形的两边长为6cm，8cm，则它的第三边长是．

查看试题解析
17. 如图，平移图形M，使其与图形N可以拼成一个平行四边形，则图中 $α$ 的度数是．

查看试题解析
18. 一个底面为30cm×30cm的长方体玻璃容器中装满水，现将一部分水倒入一个底面为正方形、高为10cm的铁桶中，当铁桶装满水时，容器中的水面下降了20cm，铁桶的底面边长是厘米. （保留根号）

查看试题解析

三、解答题

19. 计算：

(1)、 $(\sqrt{8} + \sqrt{3}) \times \sqrt{6} - 4 \sqrt{\frac{1}{2}}$ ；

(2)、 $\frac{\sqrt{12} \times \sqrt{6}}{\sqrt{18}} + (\sqrt{6} + 2) (2 - \sqrt{6})$ .

查看试题解析
20. 如图，已知矩形ABCD的对角线AC和BD相交于点O， AC＝2AB．求∠AOD的度数．

查看试题解析
21. 如图，矩形ABCD中，O为BD中点，PQ过点O分别交AD、BC于点P、Q，连接BP和DQ，求证：四边形PBQD是平行四边形．

查看试题解析
22. 在B港有甲、乙两艘渔船，若甲船沿北偏东60°的方向以每小时8海里的速度前进，乙船沿南偏东某个角度的方向以每小时15海里的速度前进，2小时后，甲船到M岛，乙船到P岛，两岛相距34海里，你知道乙船是沿哪个方向航行的吗？

查看试题解析
23. 如图，四边形ABCD是菱形，BE⊥AD，BF⊥CD，垂足分别为点E，F．

(1)、求证：BE＝BF；

(2)、当菱形ABCD的对角线AC＝8，BD＝6时，求BE的长．

查看试题解析
24. 阅读下列解题过程：
$\frac{1}{\sqrt{5} + \sqrt{4}} = \frac{1 \times (\sqrt{5} - \sqrt{4})}{(\sqrt{5} + \sqrt{4}) (\sqrt{5} - \sqrt{4})} = \frac{\sqrt{5} - \sqrt{4}}{{(\sqrt{5})}^{2} - {(\sqrt{4})}^{2}} = \sqrt{5} - \sqrt{4} = \sqrt{5} - 2$ ；
$\frac{2}{\sqrt{6} - \sqrt{5}} = \frac{2 \times (\sqrt{6} + \sqrt{5})}{(\sqrt{6} - \sqrt{5}) (\sqrt{6} + \sqrt{5})} = \frac{2 \sqrt{6} + 2 \sqrt{5}}{{(\sqrt{6})}^{2} - {(\sqrt{5})}^{2}} = 2 \sqrt{6} + 2 \sqrt{5}$ ；
请解答下列问题：

(1)、观察上面解题过程，计算 $\frac{3}{\sqrt{10} - \sqrt{7}}$ ；

(2)、请直接写出 $\frac{1}{\sqrt{n} + \sqrt{n - 1}}$ 的结果（ $n \geq 1$ ）

(3)、利用上面的解法，请化简： $\frac{1}{1 + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{4}} + \cdot \cdot \cdot + \frac{1}{\sqrt{98} + \sqrt{99}} + \frac{1}{\sqrt{99} + \sqrt{100}}$ ．

查看试题解析
25. 如图，在四边形ABCD中， $A B ∥ C D$ ， ∠A＝90°，AB＝24cm，AD＝6cm，CD＝28cm．点P从点A出发，以2cm/秒的速度向点B运动；点Q从点C出发，以4cm/秒的速度向点D运动．规定其中一个点到达终点时，另一点也随之停止运动．设Q点运动的时间为t秒．

(1)、若P，Q两点同时出发．
①当四边形APQD为矩形时，求出t值；
②当四边形BCQP为平行四边形时，求t的值；

(2)、若P点先运动2秒后停止运动．此时Q点从C点出发，到达D点后运动立即停止．则t为时三角形DPQ为直角三角形（直接写出结果）．

查看试题解析
26. 如图，在 $R t △ A B C$ 中，过点 $C$ 的直线 $M N ∥ A B$ ， $D$ 为 $A B$ 边上一点、过点 $D$ 作 $D E ⊥ B C$ ，交直线 $M N$ 于 $E$ ，垂足为 $F$ ，连接 $C D$ 、 $B E$ .

(1)、求证： $C E = A D$ ；

(2)、当 $D$ 在 $A B$ 中点时，四边形 $B E C D$ 是什么特殊四边形？说明你的理由；

(3)、若 $D$ 为 $A B$ 中点，则当 $∠ A =$ 时，四边形 $B E C D$ 是正方形（直接写出答案）.

查看试题解析