河北省邢台市信都区2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-02-22 类型：期中考试

进入出卷网下载

一、单选题

1. 计算 $a^{2} \cdot a^{3} \cdot a^{4}$ 的结果是（）．

A、 $a^{9}$ B、a¹⁰ C、 $a^{20}$ D、 $a^{24}$

查看试题解析
2. 如图，直线 $a ∥ b$ ，则直线 $a ， b$ 之间的距离是（）

A、线段 $A B$ B、线段 $A B$ 的长度 C、线段 $C D$ D、线段 $C D$ 的长度

查看试题解析
3. $3^{- 2}$ 与3²之间的关系是（）．

A、相等 B、互为相反数 C、互为倒数 D、和为1

查看试题解析
4. 将3x-2y=1变形，用含x的代数式表示y，正确的是（）

A、 $x = \frac{1 + 2 y}{3}$ B、 $y = \frac{3 x - 1}{2}$ C、 $y = \frac{1 - 3 x}{2}$ D、 $x = \frac{1 - 2 y}{3}$

查看试题解析
5. 计算 ${(3 a^{3})}^{2}$ 的结果是（）

A、 $9 a^{6}$ B、 $9 a^{5}$ C、 $6 a^{6}$ D、 $6 a^{5}$

查看试题解析
6. 下列四组图形中，平移其中一个三角形可以得到另一个三角形的一组图形是（　　）

A、 B、 C、 D、

查看试题解析
7. 若甲数为x，乙数为y，则“甲数的3倍比乙数的一半少2”，列成方程是（）

A、 $3 x + \frac{1}{2} y = 2$ B、 $3 x - \frac{1}{2} y = 2$ C、 $\frac{1}{2} y - 3 x = 2$ D、 $\frac{1}{2} y + 2 = 3 x$

查看试题解析
8. 若二元一次方程组 ${\begin{array}{l} 4 x - 3 y = 13 \\ \otimes \end{array}$ 的解为 ${\begin{array}{l} x = 1 \\ y = - 3 \end{array}$ ，则 $\otimes$ 表示的方程可以是（）．

A、 $x + y = 4$ B、 $x - y = 4$ C、 $x y = 3$ D、 $2 x + y = 1$

查看试题解析
9. 命题是能够判断真假的语句，命题一般都有题设与结论．命题“垂直于同一条直线的两条直线互相平行”的题设是（）．

A、两条直线互相平行 B、两条直线互相垂直 C、同一条直线 D、两条直线垂直于同一条直线

查看试题解析
10. 如图， $∠ 1$ 与 $∠ 2$ 的关系是（）

A、互为对顶角 B、互为同位角 C、互为内错角 D、互为同旁内角

查看试题解析
11. 观察下列两个多项式相乘的运算过程：

根据你发现的规律，若（x+a）（x+b）=x²-7x+12，则a ， b的值可能分别是（）

A、 $- 3$ ， $- 4$ B、 $- 3$ ，4 C、3， $- 4$ D、3，4

查看试题解析
12. 利用加减消元法解方程组 ${\begin{array}{l} 2 x + 3 y = - 6 ① \\ 3 x - 2 y = 4 ② \end{array}$ ，下列做法正确的是（）

A、要消去y可以将①×2﹣②×3 B、要消去x，可以将①×3+②×2 C、要消去y，可以将①×2+②×（﹣3） D、要消去x，可以将①×3﹣②×2

查看试题解析
13. 如图所示，将如图一所示的大小相同的四个小正方形按图二所示的方式放置在一个边长为a的大正方形中，中间恰好空出两条互相垂直的宽都为b的长方形，根据图二中阴影部分的面积计算方法可以验证的公式为（）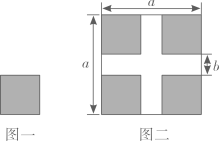

A、（a+b）（a﹣b）＝a²﹣b² B、（a+b）²＝a²+2ab+b² C、（a﹣b）²＝a²﹣2ab+b² D、（a﹣b）²＝（a+b）²﹣4ab

查看试题解析
14. 一把直尺与一块直角三角板按下图方式摆放，若 $∠ 2 = 37 °$ ，则 $∠ 1 =$ （）

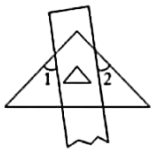A、52° B、53° C、54° D、63°

查看试题解析

二、填空题

15. 如图， $A B ⊥ B C$ ，则ABAC（填“＞”或“＝”或“＜”），其理由是．

查看试题解析
16.

(1)、计算： $2 x^{2} y \cdot (- 3 x y) =$ ．

(2)、若 $2^{x} = 12$ ， $4^{y} = 2$ ，则 $2^{x - 2 y}$ 的值为．

查看试题解析
17. 甲、乙二人分别从相距20km的A，B两地出发，相向而行．下图是小华绘制的甲、乙二人运动两次的情形，设甲的速度是x km/h，乙的速度是y km/h，根据题意所列的方程组是， $1.5 x + y =$ ．

查看试题解析

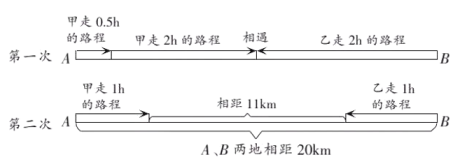
三、解答题

18. 世界上最轻的昆虫是一种卵蜂，其质量为0.000005克．

(1)、用科学记数法表示数据0.000005；

(2)、一个鸡蛋的质量大约为50克，若m只卵蜂的质量与这个鸡蛋的质量相等，请用科学记数法表示m．

查看试题解析
19. 如图，直线AB，CD相交于点O，OM⊥AB．

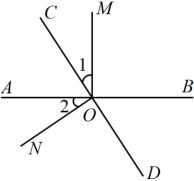(1)、若∠1=40°，求∠BOD的度数；

(2)、如果 $∠ 1 = ∠ 2$ ，那么ON与CD互相垂直吗？请说明理由．

查看试题解析
20. 以下是小鹏化简代数 $(a - 2)^{2} + (a + 1) (a - 1) - 2 a (a - 3)$ 式的过程．
解：原式= $= a^{2} - 2 a + 4 + a^{2} - 1 - 2 a^{2} + 6 a$ ………. ①
$= (a^{2} + a^{2} - 2 a^{2}) + (- 2 a + 6 a) + (4 - 1)$ ……. ②
$= 4 a + 3$ ……. ③

(1)、小鹏的化简过程在第步开始出错，错误的原因是；

(2)、请你帮助小鹏写出正确的化简过程，并计算当 $a = - \frac{1}{4}$ 时代数式的值．

查看试题解析
21. 先阅读，然后解方程组 ${\begin{array}{l} x - y - 1 = 0 \\ 4 (x - y) - y = 5 \end{array}$ .
解方程组时，可由①得x﹣y=1③，然后再将③代入②得4×1﹣y=5，求得y=﹣1，从而进一步求得 ${\begin{array}{l} x = 0 \\ y = - 1 \end{array}$ ，这种方法被称为“整体代入法”.
请用这样的方法解方程组 ${\begin{array}{l} 2 x - y - 2 = 0 \\ \frac{6 x - 3 y + 4}{5} + 2 y = 12 \end{array}$ .

查看试题解析
22. 小明家原有15头大牛和5头小牛，每天约用饲料325kg；三月后，由于经济效益好，小明父亲决定扩大养牛规模，又购进了10头大牛和5头小牛，这时每天约用饲料550kg．问每头大牛和每头小牛1天各需要多少饲料？若小明父亲估计每头大牛1天约需要饲料15～18kg，每头小牛1天约需要饲料7～8kg，你觉得小明父亲的估计准确吗？

查看试题解析
23. 如图，四边形BCED中，点A在CB的延长线上，点F在DE的延长线上，连接AF交BD于G，交CE于H，且∠1＝45，∠2＝135°．

(1)、求证：BD∥CE；

(2)、若∠C＝∠D，求证：∠A＝∠F．

查看试题解析
24. 【知识回顾】
七年级学习代数式求值时，遇到这样一类题“代数式ax﹣y+6+3x﹣5y﹣1的值与x的取值无关，求a的值”，通常的解题方法是：把x、y看作字母，a看作系数合并同类项，因为代数式的值与x的取值无关，所以含x项的系数为0，即原式＝（a+3）x﹣6y+5，所以a+3＝0，则a＝﹣3．
【理解应用】

(1)、若关于x的多项式（2x﹣3）m+2m²﹣3x的值与x的取值无关，求m值；

(2)、已知A＝（2x+1）（x﹣1）﹣x（1﹣3y），B＝﹣x²+xy﹣1，且3A+6B的值与x无关，求y的值；

(3)、【能力提升】
7张如图1的小长方形，长为a，宽为b，按照图2方式不重叠地放在大长方形ABCD内，大长方形中未被覆盖的两个部分（图中阴影部分），设右上角的面积为S₁ ，左下角的面积为S₂ ，当AB的长变化时，S₁﹣S₂的值始终保持不变，求a与b的等量关系．

查看试题解析