河北省唐山市路北区2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-02-22 类型：期中考试

进入出卷网下载

一、单选题

1. 如图，下列工具的图片中，有对顶角的是（　　）

A、 B、 C、 D、

查看试题解析
2. 在平面直角坐标系中，点A(-2，5)位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 下列各数中，立方根不等于它本身的是（）

A、2 B、1 C、0 D、－1

查看试题解析
4. 已知关于 $x$ 的方程 $2 x + k = 5$ 的解为正整数，则 $k$ 所能取得正整数的值为（）

A、2 B、1或3 C、3 D、2或3

查看试题解析
5. 方程组 ${\begin{array}{l} x + y = 5 ， \\ x - y = 3 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 2 ， \\ y = 3. \end{array}$ B、 ${\begin{array}{l} x = 3 ， \\ y = 2. \end{array}$ C、 ${\begin{array}{l} x = 4 ， \\ y = 1. \end{array}$ D、 ${\begin{array}{l} x = 1 ， \\ y = 4. \end{array}$

查看试题解析
6. 下列各式正确的是（）

A、 $(- 2)^{2} = 4$ B、 $\sqrt{4} = \pm 2$ C、 $- 2^{2} = 4$ D、 $\sqrt[3]{- 8} = 2$

查看试题解析
7. 如图所示，下列四个选项中错误的是（）

A、∠1与∠2是同旁内角 B、∠2与∠3是邻补角 C、∠1与∠4是内错角 D、∠3与∠5是对顶角

查看试题解析
8. 下列数据不能确定物体位置的是（）

A、4行5列 B、东北方向 C、青年东路25号 D、东经118°，北纬40°

查看试题解析
9. 点 $P (2 ， - 3)$ 向左平移3个单位，向上平移2个单位到点 $Q$ ，则点 $Q$ 的坐标为（）

A、 $(- 1 ， - 1)$ B、 $(- 1 ， - 5)$ C、 $(5 ， - 1)$ D、 $(5 ， - 5)$

查看试题解析
10. 实数 $\sqrt{2} + 1$ 在数轴上的对应点可能是（）

A、 $A$ 点 B、 $B$ 点 C、 $C$ 点 D、 $D$ 点

查看试题解析
11. 如图所示，点 $E$ 在 $A C$ 的延长线上，下列条件中能判断 $B D // A C$ 的是（）

A、 $∠ 3 = ∠ A$ B、 $∠ D = ∠ D C E$ C、 $∠ 1 = ∠ 2$ D、 $∠ A + ∠ A C D = 180 °$

查看试题解析
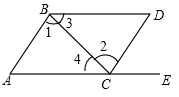12. 已知实数 $a$ ， $b$ 在数轴上的位置如图所示，下列结论中正确的是（）

A、 $a > b$ B、 $| a | < | b |$ C、 $a b > 0$ D、 $- a > b$

查看试题解析
13. 如图，利用平面直角坐标系画出的正方形网格中，若 $A (1 ， 2)$ ， $B (2 ， 1)$ ，则点C的坐标为（）

A、 $(1 ， - 3)$ B、 $(2 ， - 1)$ C、 $(3 ， 1)$ D、 $(3 ， - 1)$

查看试题解析
14. 如图是雷达在一次探测中发现的三个目标，其中目标A，B的位置分别表示为（120°，5），（240°，4），按照此方法可以将目标C的位置表示为（）

A、（30°，1） B、（210°，6） C、（30°，6） D、（60°，2）

查看试题解析

二、填空题

15. 点A（3，﹣2）到x轴的距离是．

查看试题解析
16. 如图，用符号语言表达定理“内错角相等，两直线平行”的推理形式：
∵ ， ∴a∥b．

查看试题解析
17. 已知x，y满足方程组 ${\begin{array}{l} 4 x + 3 y = - 1 \\ 2 x + y = 3 \end{array}$ ，则x+y的值为．

查看试题解析
18. 某景点拟在如图所示的长方形荷塘上架设小桥．若荷塘周长为280m，且桥宽忽略不计，则小桥总长为m．

查看试题解析

三、解答题

19. 计算

(1)、计算： $- \sqrt[3]{- 8} + \sqrt[3]{125} + \sqrt{{(- 2)}^{2}}$ ．

(2)、求x的值： $(x - 1)^{2} = 25$ ．

查看试题解析
20. 解方程组：

(1)、 ${\begin{array}{l} 3 x + y = 5 \\ 4 x - y = 9 \end{array}$

(2)、 ${\begin{array}{l} 2 x + y = 13 \\ 4 x - 3 y = 11 \end{array}$

查看试题解析
21. 按要求完成下列推理证明.
如图，已知点D为BC延长线上一点，CE∥AB.

求证：∠A+∠B+∠ACB＝180°

证明：∵CE∥AB，

∴∠1＝ ▲ ，（）

∠2＝ ▲ ，（）

又∠1+∠2+∠ACB＝180°（平角的定义），

∴∠A+∠B+∠ACB＝180°

查看试题解析
22. 已知：点P(2m+4，m-1).试分别根据下列条件，求出P点的坐标.

(1)、点P在y轴上；

(2)、点P的纵坐标比横坐标大3；

(3)、点P在过A(2，-4)点且与x轴平行的直线上.

查看试题解析
23. 喜欢探究的亮亮同学拿出形状分别是长方形和正方形的两块纸片，其中长方形纸片的长为 $3 d m$ ，宽为 $2 d m$ ，且两块纸片面积相等．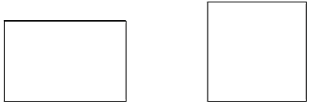

(1)、亮亮想知道正方形纸片的边长，请你帮他求出正方形纸片的边长；（结果保留根号）

(2)、在长方形纸片上截出两个完整的正方形纸片，面积分别为 $2 d m^{2}$ 和 $3 d m^{2}$ ，亮亮认为两个正方形纸片的面积之和小于长方形纸片的总面积，所以一定能截出符合要求的正方形纸片来，你同意亮亮的见解吗？为什么？（参考数据： $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732$ ）

查看试题解析
24. 如图，在四边形 ABCD 中，BE 平分∠ABC，∠AEB=∠ABE．

(1)、求∠D 与∠C 的数量关系；

(2)、若∠C=∠A，判断 AB 与 CD 的位置关系，并说明理由．

查看试题解析
25. 如图，已知在平面直角坐标系中，OA＝OB＝4，BC＝12，点P的坐标是（a，6）．

(1)、直接写出 $△$ ABC顶点A，C的坐标；

(2)、若点P坐标为（1，6），连接PA，PB，求 $△$ PAB的面积；

(3)、是否存在点P，使 $△$ PAB的面积等于 $△$ ABC的面积？如果存在，请求出点P的坐标．

查看试题解析
26. 如图，AC，BD被AB所截，E为AB外一点，连接CE，ED，已知∠A= （90 + x）°，∠B=（90 – x）°，∠CED=90°，2∠C –∠D = $α °$ ．

(1)、判断AC与BD的位置关系，并说明理由；

(2)、当 $α$ =30时，求∠C，∠D的度数；

(3)、直接写出∠C，∠D的度数（用含 $α$ 的式子表示）．

查看试题解析