河北省唐山市乐亭县2021-2022学年七年级下学期期中考试数学试题

试卷更新日期：2023-02-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下面的各组图案中，不能由其中一个经过平移后得到另一个的是（）．

A、 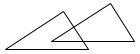B、 C、 D、

查看试题解析
2. 方程2x-3y=7，用含x的代数式表示y为（）

A、y= $\frac{1}{3}$ （7-2x） B、y= $\frac{1}{3}$ （2x-7） C、x= $\frac{1}{2}$ （7+3y） D、x= $\frac{1}{2}$ （7-3y）

查看试题解析
3. 若方程（a+3）x+3y^|a|-2＝1是关于x， y的二元一次方程，则a的值为（）

A、－3 B、±2 C、±3 D、3

查看试题解析
4. 下列命题中，属于真命题的是（）

A、如果 $a = - 2$ ，那么 $a^{2} = 4$ B、如果 $| a | = a$ ，那么 $a > 0$ C、如果两个角相等，那么这两个角都为 $90 °$ D、同位角相等

查看试题解析
5. 已知 $a = (- 2021)^{0}$ ， $b = 2^{- 1}$ ，则a与b的大小关系为（）

A、 $a > b$ B、 $a < b$ C、 $a = b$ D、无法确定

查看试题解析
6. 如图，∠ACB＝90°，CD⊥AB，垂足为D，则点B到直线CD的距离是指（）

A、线段BC的长度 B、线段CD的长度 C、线段BE的长度 D、线段BD的长度

查看试题解析
7. 下列计算正确的是（）

A、 $x^{2} \div x^{2} = x^{2}$ B、 ${(x^{- 2})}^{2} = x^{4}$ C、 $(- 3 x)^{3} = - 27 x^{3}$ D、 $x^{- 1} \cdot x^{- 2} = x^{2}$

查看试题解析
8. 下列多项式的乘法中可用平方差公式计算的是（）

A、（1+x）（x+1） B、（-a+b）（a-b） C、（x²-y）（y²+x） D、（ $\frac{1}{2}$ a+b）（b- $\frac{1}{2}$ a）

查看试题解析
9. 方程组 ${\begin{array}{l} x - y = - 1 \\ a x - b y = 5 \end{array}$ 和方程组 ${\begin{array}{l} x + 2 y = 8 \\ a x + b y = 11 \end{array}$ 的解相同，则ab值为（）

A、2 B、4 C、6 D、8

查看试题解析
10. 如图，下列条件① $∠ 1 = ∠ 2$ ；② $∠ B A D = ∠ B C D$ ；③ $∠ 3 = ∠ 4$ ；④ $∠ B A D + ∠ A D C = 180 °$ ．其中能判定 $A B ∥ C D$ 的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 已知 $3^{m} = x$ ， $3^{2 n} = y$ ， $m$ ， $n$ 为正整数，则 $3^{m + 4 n} =$ （）

A、 $x y^{2}$ B、 $x + y^{2}$ C、 $x + y$ D、 $x y$

查看试题解析
12. 若 $(x - 4) (x + 3) = x^{2} + a x + b$ ，则 $a$ 、 $b$ 的值分别为（）

A、 $a = - 1$ ， $b = - 12$ B、 $a = 1$ ， $b = - 12$ C、 $a = - 1$ ， $b = 12$ D、 $a = 1$ ， $b = 12$

查看试题解析
13. 如图，将一个长万形纸条折成如图的形状，已知∠1=110 $°$ ，则∠2的度数为（）

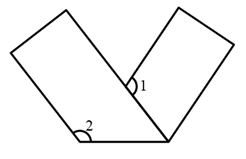A、130° B、125° C、110° D、105°

查看试题解析
14. 如图所示的是由截面为同一种长方形的墙砖粘贴的部分墙面，其中三块横放的墙砖比两块竖放的墙砖低30 cm，两块竖放的墙砖比两块横放的墙砖高50 cm，则每块墙砖的截面面积是（）

A、400 cm² B、600 cm² C、800 cm² D、900 cm²

查看试题解析
15. $2 \times (3 + 1) (3^{2} + 1) (3^{4} + 1) (3^{8} + 1) (3^{16} + 1) + 1$ 的计算结果是（）

A、 $3^{32} + 1$ B、 $3^{32} - 1$ C、 $3^{31}$ D、 $3^{32}$

查看试题解析
16. 如图，已知 $A B ∥ C D$ ， $E F ⊥ A B$ 于点 $E$ ， $∠ A E H = ∠ F G H = 20 °$ ， $∠ H = 50 °$ ，则 $∠ E F G$ 的度数是（）

A、 $120 °$ B、 $130 °$ C、 $140 °$ D、 $150 °$

查看试题解析

二、填空题

17. 原子很小， $1$ 个氧原子的直径大约为 $0.000000000148 m$ ，将 $0.000000000148$ 用科学记数法表示为.

查看试题解析
18. 如图， $O A ⊥ O B$ 于 $O$ ，直线 $C D$ 经过 $O$ ， $∠ A O D = 35 °$ ，则 $∠ B O C$ 的度数是．

查看试题解析
19. 李明、王超两位同学同时解方程组 ${\begin{array}{l} a x + b y = 2 \\ m x - 7 y = - 9 \end{array}$ 李明解对了，得 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$ ，王超抄错了m得 ${\begin{array}{l} x = - 2 \\ y = - 2 \end{array}$ 则原方程组中a的值为．

查看试题解析
20. 已知如图，直线 $C B ∥ O A$ ， $∠ C = ∠ O A B = 120 °$ ， $E$ 、 $F$ 在 $C B$ 上，且满足 $∠ F O B = ∠ A O B$ ， $O E$ 平分 $∠ C O F$ ．

(1)、若平行移动 $A B$ ，那么 $∠ O B C ： ∠ O F C$ 的值是；

(2)、在平行移动 $A B$ 的过程中，当 $∠ C O E =$ （度）时， $∠ O E C = ∠ O B A$ ．

查看试题解析

三、解答题

21. 解方程组： ${\begin{array}{l} 5 x + y = 2 \\ x - 3 y = 4 \end{array}$ （用加减消元法）．

查看试题解析
22. 如图，已知EF $∥$ AB，∠DEF=∠A．

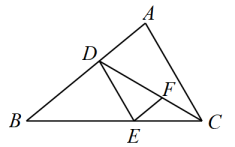(1)、求证：DE $∥$ AC；

(2)、若CD平分∠ACB，∠BED=60°，求∠ACD的度数．

查看试题解析
23. 已知多项式 $A = {(x + 2)}^{2} + x (x - 2) - (x + 3) (x - 3)$

(1)、化简多项式 $A$ 时，小明的结果与其他同学的不同，请你检查小明同学的解题过程．
小明的作业：
解： $A = {(x + 2)}^{2} + x (x - 2) - (x + 3) (x - 3)$
$x^{2} \underline{+ 2 x} + 4 ① + x^{2} \underline{- 2 x} ② - x^{2} \underline{- 9} ③$
$= x^{2} - 5$
在标出①②③的几项中，出现错误的是，请写出正确的解答过程；

(2)、小亮说：“只要给出 $x^{2} + 2 x + 1$ 的合理的值，即可求出多项式 $A$ 的值．”小明给出 $x^{2} + 2 x + 1$ 的值为4，请你求出此时 $A$ 的值．

查看试题解析
24. 如图，有三个论断：① $∠ 1 = ∠ 2$ ；② $∠ B = ∠ C$ ；③ $∠ A = ∠ D$ ，请你从中任选两个作为条件，另一个作为结论构成一个命题，并证明该命题的正确性．

查看试题解析
25. 已知正数 $x$ 、 $y$ ，满足 $(x + y)^{2} = 25$ ， $x y = 4$ ．

(1)、求 $x^{2} + y^{2}$ 的值；

(2)、当 $m = (x - y)^{2}$ 时，求 $m$ 的值；

(3)、我们把形如 $a^{2} \pm 2 a b + b^{2}$ 这样的三项式称之为完全平方式，在（2）的条件下，若 $4 a^{2} + n a + m$ 是完全平方式，直接写出 $n$ 的值________．

查看试题解析
26. 面对当前疫情形势，国家迅速反应，果断决策，全民积极行动，筹款为贫因地区捐赠了一批消毒液.现要将消毒液运往该区.已知用3辆A型车和1辆B型车装满货物一次可运货9吨；用1辆A型车和2辆B型车装满货物一次可运货8吨.现有消毒液19吨.计划同时租用A型车a辆，B型车b辆，一次运完，且恰好每辆车都载满消毒液.
根据以上信息，解答下列问题：

(1)、1辆A型车和1辆B型车都载满消毒液一次可分别运送多少吨？

(2)、请你帮我们设计租车方案；

(3)、若1辆A型车需租金90元/次，1辆B型车需租金110元/次.请选出最省钱的租车方案，并求出最少租车费.

查看试题解析