河北省石家庄市新乐市2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-02-22 类型：期中考试

进入出卷网下载

一、单选题

1. 有下列方程：① $x y = 1$ ；② $2 x = 3 y$ ；③ $x - \frac{1}{y} = 2$ ；④ $x^{2} + y = 3$ ；⑤ $\frac{x}{4} = 3 y - 1$ ，其中，二元一次方程有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
2. 计算： ${(- \frac{2}{3})}^{0} =$ （）

A、 $1$ B、 $- \frac{3}{2}$ C、 $0$ D、 $\frac{2}{3}$

查看试题解析
3. 2ab•a²的计算结果是（）

A、 2ab B、4ab C、2a³b D、4a³b

查看试题解析
4. 解方程组 ${\begin{array}{l} 2 x + y = 3 ① \\ 2 x - 3 y = 4 ② \end{array}$ 时，若将①-②可得（）

A、 $- 2 y = - 1$ B、 $- 2 y = 1$ C、 $4 y = 1$ D、 $4 y = - 1$

查看试题解析
5. 如图，直线m $∥$ n，则∠α为（）

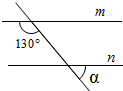A、70° B、65° C、50° D、40°

查看试题解析
6. 计算： $199 \times 201 =$ （）

A、 $3999$ B、 $4179$ C、 $41790$ D、 $39999$

查看试题解析
7. 如图，直线AB ， CD相交于点O ， OE平分∠AOC ，若∠BOD=70°，则∠DOE的度数是（）

A、70° B、35° C、120° D、145°

查看试题解析
8. 下列计算：① $(4 x^{3})^{2} = 8 x^{6}$ ；② $(- 5 a^{5} b^{5})^{2} = 25 a^{10} b^{10}$ ；③ $(- \frac{2}{3} x)^{3} = - \frac{8}{3} x^{3}$ ；④ $(3 x^{2} y^{3})^{4} = 81 x^{6} y^{12}$ $．$ 其中，错误的个数是（）

A、 $1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析
9. 2021年5月国家统计局公布了第七次人口普查结果，我国人口数约为1412000000，其中数据1412000000用科学记数法表示为（）

A、 $14 .12 \times 10^{8}$ B、 $0.1412 \times 10^{10}$ C、 $1.412 \times 10^{9}$ D、 $1.412 \times 10^{8}$

查看试题解析
10. 两条直线被第三条直线所截，就第三条直线上的两个交点而言形成了“三线八角”．为了便于记忆，同学们可仿照图用双手表示“三线八角”（两大拇指代表被截直线，食指代表截线）．下列三幅图依次表示（）

A、同位角、同旁内角、内错角 B、同位角、内错角、同旁内角 C、同位角、对顶角、同旁内角 D、同位角、内错角、对顶角

查看试题解析
11. 如图，在下列条件中，不能判定直线a与b平行的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 2 = ∠ 3$ C、 $∠ 1 = ∠ 5$ D、 $∠ 3 + ∠ 4 = 180 °$

查看试题解析
12. 已知 $a = 8 1^{31}$ ， $b = 2 7^{41}$ ， $c = 9^{61}$ ，则 $a ， b ， c$ 的大小关系是（）

A、 $a > b > c$ B、 $a > c > b$ C、 $c > b > a$ D、 $b > c > a$

查看试题解析
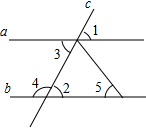13. 若关于x，y的方程组 ${\begin{array}{l} a x - b y = - 4 \\ a x + b y = 8 \end{array}$ 的解是 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$ ，则方程组 ${\begin{array}{l} a (x + 3) - b (y - 1) = - 4 \\ a (x + 3) + b (y - 1) = 8 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = - 1 \\ y = 4 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$ C、 ${\begin{array}{l} x = 1 \\ y = - 4 \end{array}$ D、 ${\begin{array}{l} x = 5 \\ y = 2 \end{array}$

查看试题解析
14. 《九章算术》是中国传统数学的重要著作，书中有一道题“今有五雀六燕，集称之衡，雀俱重，燕俱轻；一雀一燕交而处，衡适平；并燕雀重一斤.问：燕雀一枚，各重几何？”译文：“五只雀、六只燕，共重1斤（古时1斤＝16两）.雀重燕轻，互换其中一只，恰好一样重，问：每只雀、燕重量各为多少？”设雀重x两，燕重y两，可列出方程组（）

A、 ${\begin{array}{l} 5 x + 6 y = 16 \\ 4 x + y = 5 y + x \end{array}$ B、 ${\begin{array}{l} 5 x + 6 y = 10 \\ 4 x + y = 5 y + x \end{array}$ C、 ${\begin{array}{l} 5 x + 6 y = 10 \\ 5 x + y = 6 y + x \end{array}$ D、 ${\begin{array}{l} 5 x + 6 y = 16 \\ 5 x + y = 6 y + x \end{array}$

查看试题解析
15. 一次抽奖活动特等奖的中奖率为 $\frac{1}{50000}$ ,把 $\frac{1}{50000}$ 用科学记数法表示为（　　）

A、 $5 \times 10^{﹣ 4}$ B、 $5 \times 10^{﹣ 5}$ C、 $2 \times 10^{﹣ 4}$ D、 $2 \times 10^{﹣ 5}$

查看试题解析
16. 如图：AB∥CD，OE平分∠BOC，OF⊥OE，OP⊥CD，∠ABO＝40°，则下列结论：①OF平分∠BOD；②∠POE＝∠BOF；③∠BOE＝70°；④∠POB＝2∠DOF，其中结论正确的序号是（）

A、①②③ B、①②④ C、①③④ D、①②③④

查看试题解析

二、填空题

17. $0.125 \times 8 =$ ； $0.12 5^{5} \times 8^{6} =$ ．

查看试题解析
18. 已知 $110 b^{2} \div (- 5 b)^{m} = A$ ，若 $m = 1$ ，则 $A =$ ；若 $m = 3$ ，则 $A =$ ．

查看试题解析
19. 现有甲、乙、丙三种不同的矩形纸片（边长如图）．

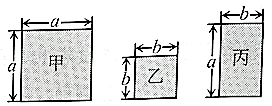(1)、取甲、乙纸片各1块，其面积和为；

(2)、嘉嘉要用这三种纸片紧密拼接成一个大正方形，先取甲纸片1块，再取乙纸片4块，还需取丙纸片块．

查看试题解析

三、解答题

20. 解方程组

(1)、 ${\begin{array}{l} 4 f + g = 15 \\ 3 g - 4 f = - 3 \end{array}$

(2)、 ${\begin{array}{l} 2 x + 3 y = 3 \\ 3 x - 2 y = 11 \end{array}$

(3)、 ${\begin{array}{l} \frac{2 (x - y)}{3} - \frac{x + y}{4} = - 1 \\ 6 (x + y) - 4 (2 x - y) = 16 \end{array}$

查看试题解析
21.

(1)、计算：
①（a+b）（a-2b）-（a+2b）（a-b）；
②（a-2b）（a²+2ab+4b）；

(2)、先化简，再求值：（x-2）²-4x（x-1）+（2x+1）（2x-1），其中x=1．

查看试题解析
22. 如图，在四边形ABCD中，E、F分别是CD、AB延长线上的点，连结EF，分别交AD、BC于点G、H．若∠1＝∠2，∠A＝∠C，试说明AD∥BC和AB∥CD．
请完成下面的推理过程，并填空（理由或数学式）：
∵∠1＝∠2（  ）
∠1＝∠AGH（  ）
∴∠2＝∠AGH（  ）
∴AD∥BC（  ）
∴∠ADE＝∠C（  ）
∵∠A＝∠C（  ）
∴∠ADE＝∠A
∴AB∥CD（  ）

查看试题解析
23. 小红准备完成题目：计算（x²x+2）（x²-x）．她发现第一个因式的一次项系数被墨水遮挡住了．

(1)、她把被遮住的一次项系数猜成3，请你完成计算：（x²+3x+2）（x²-x）；

(2)、老师说：“你猜错了，这个题目的正确答案是不含三次项的．”请通过计算说明原题中被遮住的一次项系数是多少？

查看试题解析
24. 为了提倡节约用水，某市制定了两种收费方式：当每户每月用水量不超过 $12 m^{3}$ 时，按一级单价收费；当每户每月用水量超过 $12 m^{3}$ 时，超过部分按二级单价收费.已知李阿姨家五月份用水量为 $10 m^{3}$ ，缴纳水费32元.七月份因孩子放假在家，用水量为 $14 m^{3}$ ，缴纳水费51.4元.

(1)、问该市一级水费，二级大费的单价分别是多少？

(2)、某户某月缴纳水费为64.4元时，用水量为多少？

查看试题解析
25. 小明同学遇到这样一个问题：
如图①，已知： $A B ∥ C D$ ， $E$ 为 $A B$ 、 $C D$ 之间一点，连接 $B E$ ， $E D$ ，得到 $∠ B E D$ ．
求证： $∠ B E D = ∠ B + ∠ D$ ．
小亮帮助小明给出了该问的证明．
证明：过点 $E$ 作 $E F ∥ A B$ ，则有 $∠ B E F = ∠ B$ ．
∵ $A B ∥ C D$ ，
∴ $E F ∥ C D$ ，
$∴ ∠ F E D = ∠ D$ ，
$∴ ∠ B E D = ∠ B E F + ∠ F E D = ∠ B + ∠ D$ ．
请你参考小亮的思考问题的方法，解决问题：
直线 $l_{1} ∥ l_{2}$ ，直线 $E F$ 和直线 $l_{1}$ 、 $l_{2}$ 分别交于 $C$ 、 $D$ 两点，点 $A$ 、 $B$ 分别在直线 $l_{1}$ 、 $l_{2}$ 上

(1)、猜想：如图②，若点 $P$ 在线段 $C D$ 上， $∠ P A C = 15 °$ ， $∠ P B D = 40 °$ ，求 $∠ A P B$ 的度数．

(2)、拓展：如图③，若点 $P$ 在直线 $E F$ 上，连接 $P A$ 、 $P B$ $(B D < A C)$ ，直接写出 $∠ P A C$ 、 $∠ A P B$ 、 $∠ P B D$ 之间的数量关系．

查看试题解析