河北省石家庄市平山县2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-02-22 类型：期中考试

进入出卷网下载

一、单选题

1. 在下列四个图案中，能用平移变换来分析其形成过程的图案是（）

A、 B、 C、 D、

查看试题解析
2. 下列各数中，无理数是（）

A、 $\sqrt{4}$ B、 $3.14$ C、 $\sqrt[3]{- 27}$ D、 $5 π$

查看试题解析
3. 在平面直角坐标系中，点P（3，－7）所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 下列各式中，计算正确的是（）

A、 $\pm \sqrt{16} = 4$ B、 $\sqrt{16} = \pm 4$ C、 $- \sqrt{16} = - 4$ D、 $\pm \sqrt{16} = \pm 8$

查看试题解析
5. 如图所示，直线a、b被直线c所截，现给出下列四种条件：①∠2＝∠6②∠2＝∠8③∠1＋∠4＝180°④∠3＝∠8，其中能判断是a∥b的条件的序号是（）

A、①② B、①③ C、①④ D、③④

查看试题解析
6.
如图，将三角板的直角顶点放在直尺的一边上，若∠1=65°，则∠2的度数为（　　）

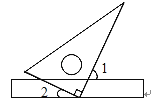A、10° B、15° C、25° D、35°

查看试题解析
7. 在平面直角坐标系中，点 $P$ 的横坐标是-3且点 $P$ 到 $x$ 轴的距离为5，则点 $P$ 的坐标是（）

A、（5，-3）或（-5，-3） B、（-3，5）或（-3，-5） C、（-3，5） D、（-3，-5）

查看试题解析
8.
如图，若象棋盘上建立直角坐标系，使“将”位于点（1，﹣2），“象”位于点（3，﹣2），那么“炮”位于点（　　）

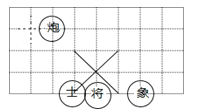A、（1，﹣1） B、（﹣1，1） C、（﹣1，2） D、（1，﹣2）

查看试题解析
9. 如图，将半径为2cm的半圆水平向左平移2cm，则半圆所扫过的面积（阴影部分）为（）
.

A、 $π c m^{2}$ B、 $4 c m^{2}$ C、 $(π - \frac{π}{2})$ cm² D、 $(π + \frac{π}{2})$ cm²

查看试题解析
10. 数轴上1， $\sqrt{3}$ 的点分别为A和B，若A为BC的中点，则点C表示的数是（）

A、 $1 - \sqrt{3}$ B、 $\sqrt{3} - 1$ C、 $2 - \sqrt{3}$ D、 $\sqrt{3} - 2$

查看试题解析
11. 图所示，在四边形ABCD中，BD是它的一条对角线，若∠1＝∠2，∠A＝55°，则∠ADC＝（）

A、110° B、115° C、125° D、135°

查看试题解析
12. 已知甲、乙、丙三个数，甲=5+ $\sqrt{13}$ ，乙=2+ $\sqrt{19}$ ，且甲＞丙＞乙，则下列符合条件的丙是（）

A、1+ $\sqrt{23}$ B、4+ $\sqrt{26}$ C、4+ $\sqrt{15}$ D、4+ $\sqrt{3}$

查看试题解析
13. 第二象限内的点P（x，y）满足|x|＝9，y²＝4，则点P 的坐标是（）

A、 $(- 9 ， 2)$ B、 $(9 ， 2) ； (9 ， - 2)$ C、 $(- 9 ， 2) ； (- 9 ， - 2)$ D、 $(9 ， - 2)$

查看试题解析
14. 线段MN是由线段EF经过平移得到的，若点E(﹣1，3)的对应点M(2，5)，则点F(﹣3，﹣2)的对应点N的坐标是（）

A、(﹣1，0) B、(﹣6，0) C、(0，﹣4) D、(0，0)

查看试题解析
15. 如图，若直线a∥b，那么∠x＝（）

A、50° B、64° C、72° D、75°

查看试题解析
16. 如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆 O₁ ， O₂ ， O₃ ， …组成一条平滑的曲线，点P 从原点O 出发，沿这条曲线向右运动，速度为每秒 $\frac{π}{2}$ 个单位长度，则第2022秒时，点P 的坐标是（）

A、 $(1011 π ， 0)$ B、 $(1011 π ， 1)$ C、 $(2022 ， - 1)$ D、 $(2022 ， 0)$

查看试题解析

二、填空题

17. （﹣0.7）² 的平方根是．

查看试题解析
18.
如图，有下列判断：①∠A与∠1是同位角；②∠A与∠B是同旁内角；③∠4与∠1是内错角；④∠1与∠3是同位角．其中正确的是（填序号）．

查看试题解析
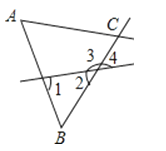19. 下列各图中的 MA₁与NAn平行．

(1)、图①中的∠A₁＋∠A₂＝180°，图②中的∠A₁＋∠A₂＋∠A₃＝360°，图③中的∠A₁＋∠A₂＋∠A₃＋∠A₄＝540°，图④中的∠A₁＋∠A₂＋∠A₃＋∠A₄＋∠A₅＝°，第⑩个图中的∠A₁＋∠A₂＋∠A₃＋…＋∠A₁₀＝°；

(2)、第n 个图中的∠A₁＋∠A₂＋∠A₃＋…＋∠An＝°．

查看试题解析

三、解答题

20. 计算：

(1)、 $\sqrt{81} + \sqrt[3]{- 27} + \sqrt{{(- \frac{2}{3})}^{2}}$

(2)、 $| \sqrt{2} - \sqrt{3} | + 2 \sqrt{2}$

查看试题解析
21. 如图，直线 $A B$ 、 $C D$ 相交于点 $O$ ， $O P ⊥ C D$ ， $∠ A O P$ 与 $∠ B O D$ 的度数之比为 $3 ： 2$ ．求 $∠ A O C$ 的度数．

查看试题解析
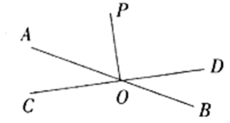22. 在平面直角坐标系中，A、B、C三点的坐标分别为（-6，7）、（-3，0）、（0，3）．

(1)、画出△ABC；

(2)、在△ABC中，点C经过平移后的对应点为C′（5，4），将△ABC作同样的平移得到△A′B′C′，画出平移后的△A′B′C′，并写出点 A′的坐标 ▲ ；

(3)、P（-3，m）为△ABC 中一点，将点P 向右平移4个单位后，再向下平移7个单位得到点Q（n，-3），则 m＝， n＝．

查看试题解析
23. 如图，∠B=∠ADE，∠EDC=∠GFB，GF⊥AB，求证：CD⊥AB.

查看试题解析
24. 已知，如图，AB∥CD，EG平分∠BEF，FG平分∠EFD，求∠EGF 的度数．

查看试题解析
25. 如图，以直角三角形 $A O C$ 的直角顶点 $O$ 为原点，以 $O C 、 O A$ 所在直线为 $x$ 轴， $y$ 轴建立平面直角坐标系，点 $A (0 ， a) ， C (c ， 0)$ 满足 $\sqrt{a - 2 c} + | c - 4 | = 0$

(1)、则 $C$ 点的坐标为； $A$ 点的坐标为．

(2)、直角三角形 $A O C$ 的面积为．

(3)、已知坐标轴上有两动点 $P 、 Q$ 同时出发， $P$ 点从 $C$ 点出发沿 $x$ 轴负方向以1个单位长度每秒的速度匀速移动， $Q$ 点从 $O$ 点出发以2个单位长度每秒的速度沿 $y$ 轴正方向移动，点 $Q$ 到达 $A$ 点整个运动随之结束． $A C$ 的中点 $D$ 的坐标是 $(2 ， 4)$ ，设运动时间为t（t＞0）秒，问：是否存在这样的t使 $S_{△ O D P} = S_{△ O D Q}$ ？若存在，请求出 $t$ 的值；若不存在，请说明理由．

查看试题解析
26. 如图，平面内的直线有相交和平行两种位置关系.

(1)、如图(a)，已知AB∥CD，求证：∠BPD=∠B+∠D.

(2)、如图(b)，已知AB∥CD，求证：∠BOD=∠P+∠D.

(3)、根据图(c)，试判断∠BPD，∠B，∠D，∠BQD之间的数量关系，并说明理由.

查看试题解析