河北省保定市定州市2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-02-22 类型：期中考试

进入出卷网下载

一、单选题

1. $\sqrt{\frac{9}{16}}$ 的值等于（）

A、± $\frac{3}{4}$ B、－ $\frac{3}{4}$ C、 $\frac{3}{4}$ D、 $\frac{81}{4}$

查看试题解析
2. 在实数 $\frac{22}{7}$ 、 $\sqrt{9}$ 、 $\sqrt{11}$ 、 $π$ 、 $\sqrt[3]{8}$ 中，无理数的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 平面直角坐标系内有一点 $P (- 2022 ， - 2022)$ ，则点P在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 如图，直线AB∥CD，∠1＝50°，则∠2＝（）

A、40° B、50° C、100° D、130°

查看试题解析
5. 在平面直角坐标系中，将点A（1，﹣2）向上平移3个单位长度，再向左平移2个单位长度，得到点A′，则点A′的坐标是（）

A、（﹣1，1） B、（﹣1，﹣2） C、（﹣1，2） D、（1，2）

查看试题解析
6. 在数轴上标注了四段范围，如图，则表示 $\sqrt{7}$ 的点落在（）

A、段① B、段② C、段③ D、段④

查看试题解析
7. 如图，△ABC沿直线BC向右平移得到△DEF，已知EC=2，BF=8，则CF的长为（）

A、3 B、4 C、5 D、6

查看试题解析
8. 下列说法错误的是（）

A、1的平方是1 B、0的平方根是0 C、 ${(- 2)}^{2}$ 的平方根是 $- 2$ D、 $- 1$ 的立方根是 $- 1$

查看试题解析
9. 如图，现将一块含有 $3 0^{∘}$ 角的直角三角板的一个顶点放在直尺的一边上，若 $∠ 1 = 2 ∠ 2$ ，那么 $∠ 1$ 的度数为（）

A、 $5 0^{∘}$ B、 $6 0^{∘}$ C、 $7 0^{∘}$ D、 $8 0^{∘}$

查看试题解析
10. 如图是某次行车路线，共拐了三次弯，最后行车路线与开始的路线是平行的，已知第一次转过的角度120°，第三次转过的角度135°，则第二次转过的角度是（）

A、105° B、120° C、135° D、75°

查看试题解析
11. 已知点 $A$ （2，7）， $A B / / x$ 轴， $A B = 3$ ，则 $B$ 点的坐标为（）

A、（5，7） B、（2，10） C、（2，10）或（2，4） D、（5，7）或（-1，7）

查看试题解析
12. 如图，将边长为1的正方形依次放在坐标系中，其中第一个正方形的两边OA₁ ， OA₃分别在y轴和x轴上，第二个正方形的一边A₃A₄与第一个正方形的边A₂A₃共线，一边A₃A₆在x轴上……以此类推，则点A₂₀₂₀的坐标为（）

A、（672，-1） B、（673，-1） C、（336，1） D、（337，-1）

查看试题解析

二、填空题

13. ﹣125的立方根是．

查看试题解析
14. 已知点 $M (m + 1 ， m + 3)$ 在x轴上，则m等于.

查看试题解析
15. 如图，直线AB ， CD相交于点O ， OA平分∠EOC ， ∠EOD=120°，则∠BOD=°．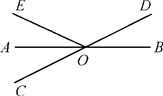

查看试题解析
16. 若x、y为实数，且满足 $| 2 x + 3 | + \sqrt{9 - 4 y} = 0$ ，则xy的立方根为．

查看试题解析
17. 若[ $x$ ]表示实数 $x$ 的整数部分，例如：[ $3 .5$ ]=3，则[ $\sqrt{17}$ ]= ．

查看试题解析
18. 如图直线AB、CD相交于点O，OE⊥AB，O为垂足，如果∠EOD=38°，则∠COB= ．

查看试题解析

三、解答题

19. 计算：

(1)、 $| \sqrt{2} - 1 | - | \sqrt{3} - 2 | + | \sqrt{3} - \sqrt{2} |$ ；

(2)、 $\sqrt{{(- 0.5)}^{2}} + \sqrt[3]{- 8} - \sqrt{1 \frac{9}{16}}$

查看试题解析
20. 求x的值：

(1)、 $(x - 1)^{2} = 4$ ；

(2)、 $2 (x - 1)^{3} + 16 = 0$ ．

查看试题解析
21. 如图所示的是某市区几个旅游景点的示意图（图中每个小正方形的边长为1个单位长度），若海洋极地公园的坐标为（4，0），大唐芙蓉园的坐标为（2，-1），请建立平面直角坐标系，并用坐标表示其他景点的位置．

查看试题解析
22. 如图，直线CD与直线AB相交于C，根据下列语句画图、解答．
（ 1 ）过点P作PQ $∥$ CD，交AB于点Q；
（ 2 ）过点P作PR⊥CD，垂足为R；
（ 3 ）若∠DCB=120°，猜想∠PQC是多少度？并说明理由

查看试题解析
23. 已知，E，F分别在AB和CD上，∠1＝∠D，∠2与∠C互余，AF⊥CE于G，
求证：AB $/ /$ CD．
证明：∵AF⊥CE，
∴∠CGF＝90°，
∵∠1＝∠D（已知），
∴AF∥DE（            ），
∴∠4＝  ▲  ＝90°（            ），
又∵∠2与∠C互余（已知），∠2+∠3+∠4＝180°，
∴∠2+∠C＝∠2+∠3＝90°，
∴∠C＝  ▲   ，
∴AB∥CD．（            ）

查看试题解析
24. 如图，用两个边长为 $\sqrt{8} c m$ 的小正方形剪拼成一个大的正方形，

(1)、则大正方形的边长是cm；

(2)、若沿此大正方形边的方向剪出一个长方形，能否使剪出的长方形纸片的长宽之比为3：2且面积为 $12 c m^{2}$ ，若能，试求出剪出的长方形纸片的长宽；若不能，试说明理由．

查看试题解析
25. 如图，AD⊥BC，垂足为D，点E、F分别在线段AB、BC上，EF⊥BC，∠CAD＝∠DEF，

(1)、求证：EF∥AD；

(2)、判断ED与AC的位置关系，并证明你的猜想．

查看试题解析
26. 在平面直角坐标系中，O为坐标原点，过点A（8，6）分别作x轴、y轴的平行线，交y轴于点B，交x轴于点C，点P是从点B出发，沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点，运动时间为t（秒）．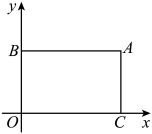

(1)、直接写出点B和点C的坐标．

(2)、当点P运动时，用含t的式子表示线段AP的长，

(3)、点D（2，0），连接PD、AD，在（2）条件下是否存在这样的t值，使 $S_{△ A P D} = \frac{1}{8} S_{四边形 A B O C}$ ，若存在，请求出t值，若不存在，请说明理由．

查看试题解析