北京市大兴区2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-02-22 类型：期中考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系 $x O y$ 中，下列各点位于第一象限的是（）

A、 $(1 ， 2)$ B、 $(1 ， - 2)$ C、 $(- 1 ， 2)$ D、 $(- 1 ， - 2)$

查看试题解析
2. 下列实数中，是无理数的是（）

A、 $- \frac{7}{22}$ B、 $\sqrt{36}$ C、 $π$ D、0.6

查看试题解析
3. 如图，数轴上点M表示的数可能是（）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、 $\sqrt{8}$ D、 $\sqrt{10}$

查看试题解析
4. 如图，直线 $A B ， C D$ 相交于点O， $O E ⊥ C D$ 于点O，若 $∠ B O D = 20 °$ ，则 $∠ A O E$ 的度数是（）

A、 $70 °$ B、 $100 °$ C、 $110 °$ D、 $160 °$

查看试题解析
5.
如图，要把河中的水引到水池A中，应在河岸B处（AB⊥CD）开始挖渠才能使水渠的长度最短，这样做依据的几何学原理是（　　）

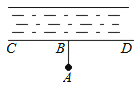A、两点之间线段最短 B、点到直线的距离 C、两点确定一条直线 D、垂线段最短

查看试题解析
6. 在下列各式中，正确的是（）

A、 $\sqrt{8} = 4$ B、 $\sqrt{2^{2}} = 2$ C、 $\sqrt{(- 2)^{2}} = - 2$ D、 $\pm \sqrt{25} = 5$

查看试题解析
7. 已知，两条直线被第三条直线所截， $∠ 1$ 和 $∠ 2$ 是同位角，若 $∠ 1 = 50 °$ ，则 $∠ 2$ 的度数是（）

A、 $∠ 2 = 50 °$ B、 $∠ 2 = 130 °$ C、 $∠ 2 = 50 °$ 或 $∠ 2 = 130 °$ D、 $∠ 2$ 的度数不能确定

查看试题解析
8. 在平面直角坐标系 $x O y$ 中，已知点 $A (2 ， 1)$ ，点B在x轴上，对于线段 $A B$ 有如下四个结论：
①线段 $A B$ 的最大值是2；
②线段 $A B$ 的最小值是1；
③线段 $A B$ 一定不经过点 $(0 ， 1)$ ；
④线段 $A B$ 可能经过点 $(5 ， - 2)$ ．
上述结论中，所有正确结论的序号是（）

A、①③ B、②③ C、①④ D、②④

查看试题解析

二、填空题

9. 49的算术平方根是．

查看试题解析
10. 若 $| x + 2 | + \sqrt{3 - y} = 0$ ，则x+y= ．

查看试题解析
11. 在比 $\sqrt{10}$ 大的实数中，最小的整数是．

查看试题解析
12. 若实数m的两个不相等的平方根是 $a + 1$ 和 $2 a - 7$ ，则实数m为．

查看试题解析
13. 如图所示，将一块三角板与一个直尺叠放，直尺的一边经过三角板的直角顶点，若 $∠ 2 = 50 °$ ，则 $∠ 1$ 的度数是 $°$ ．

查看试题解析
14. 某景区游览示意图如图所示，各个景点均在小正方形的顶点上，在社会实践活动中，七（1）班王玲同学对着景区示意图建立平面直角坐标系，描述音乐台的位置为 $(0 ， 4)$ ，东门的位置为 $(4 ， 0)$ ，则湖心亭所在位置的坐标是．

查看试题解析
15. 如图，已知 $A B ∥ C D$ ，请你添加一个条件，使得 $∠ 1 = ∠ 2$ 成立，这个条件可以是．

查看试题解析
16. 在平面直角坐标系 $x O y$ 中，对于点 $P (x ， y)$ ，我们把点 $P^{'} (- y + 2 ， x - 2)$ 叫做点P的移动点．已知点 $A_{1}$ 的移动点为 $A_{2}$ ，点 $A_{2}$ 的移动点为 $A_{3}$ ，点 $A_{3}$ 的移动点为 $A_{4}$ ， …，这样依次得到点 $A_{1} ， A_{2} ， A_{3} ， ⋯ ， A_{n} ， ⋯$ ．若点 $A_{1}$ 的坐标为 $(2 ， 1)$ ，则点 $A_{3}$ 的坐标为；若点 $A_{2022}$ 的坐标为 $(5 ， 7)$ ，则点 $A_{1}$ 的坐标为．

查看试题解析

三、解答题

17. 计算： $\sqrt{16} - \sqrt[3]{8} + \sqrt{\frac{1}{4}} \times \sqrt{100 - 64}$ ．

查看试题解析
18. 已知 $2 x^{2} - 1 = 13$ ，求实数x的值．

查看试题解析
19. 如图，已知 $∠ C A B = 80 °$ ， D是 $∠ C A B$ 平分线上一点， $D E$ 与 $A C$ 交于点E，若 $∠ E D A = 40 °$ ，求证： $E D ∥ A B$ ．
请将下面的证明过程补充完整：
证明：∵ $A D$ 平分 $∠ C A B ， ∠ C A B = 80 °$ ，
∴  ▲    ▲   $= \frac{1}{2} ∠ C A B =$   ▲  （角平分线定义）．
又∵ $∠ E D A = 40 °$ ，
∴  ▲   ．
∴ $E D ∥ A B$ （    ）．

查看试题解析
20. 如图，在一块长为 $20 m$ ，宽为 $10 m$ 的长方形草地上，修建了宽为 $1 m$ 的小路，求这块草地的绿地面积．

查看试题解析
21. 在平面直角坐标系 $x O y$ 中，已知点 $P (a - 2 ， a)$ ．

(1)、若点P在y轴上，求点P的坐标；

(2)、若点P到x轴的距离是9，求点P的坐标．

查看试题解析
22. 已知 $6 a - 3$ 的立方根是3， $3 a + b - 9$ 的算术平方根是2，求 $a^{2} - b^{2}$ 的值．

查看试题解析
23. 如图，在平面直角坐标系 $x O y$ 中，三角形 $A B C$ 的三个顶点坐标分别为 $A (2 ， 0) ， B (2 ， 6) ， C (- 1 ， 2)$ ，点 $A^{'}$ 的坐标是 $(- 2 ， - 1)$ ，现将三角形 $A B C$ 平移，使点A平移到点 $A^{'}$ 处， $B^{'} ， C^{'}$ 分别是B，C的对应点．

(1)、根据题意，画出平移后的三角形 $A^{'} B^{'} C^{'}$ （不写画法），并直接写出 $B^{'}$ 的坐标；

(2)、求三角形 $A B C$ 的面积；

(3)、若将C点向右平移 $m (m > 0)$ 个单位长度到点D，使得三角形 $A B D$ 的面积等于3，直接写出m的值．

查看试题解析
24. 根据下表回答下列问题：
x
17
17.1
17.2
17.3
17.4
17.5
17.6
17.7
17.8
17.9
18
$x^{2}$
289
292.41
295.84
299.29
302.76
306.25
309.76
313.29
316.84
320.41
324

(1)、316.84的平方根是；

(2)、 $\sqrt{299.3} \approx$ ；

(3)、 $\sqrt{29241} =$ ；

(4)、若 $\sqrt{n}$ 介于17.6与17.7之间，则满足条件的整数n有个；

(5)、观察表格中的数据，请写出一条你发现的结论．

查看试题解析
25. 如图，在四边形 $A B C D$ 中， $A D ∥ B C ， A B ∥ D C$ ， E是 $A B$ 延长线上一点．求证： $∠ A = ∠ C$ ．

(1)、请将下面的证明过程补充完整：
证明：∵ $A D ∥ B C$ ，
∴ $∠ A =$ ▲ （）．
∵ $A B ∥ D C$ ，
∴ ▲ （）．
∴ $∠ A = ∠ C$ ．

(2)、请根据题目条件，用与（1）不同的方法证明 $∠ A = ∠ C$ ．

查看试题解析
26. 已知三角形 $A B C ， A D ⊥ B C$ 于点D， $D M ∥ B A$ 交 $A C$ 于点M．

(1)、如图1，当点E在线段 $A B$ 上时（点E不与点A、B重合），作 $E F ⊥ B C$ 于点F，则 $∠ A D M$ 与 $∠ B E F$ 的数量关系是；

(2)、当点E在 $A B$ 的延长线上时，作 $E F$ 垂直于 $C B$ 交 $C B$ 的延长线于点F．
①依题意补全图2；
②猜想 $∠ A D M$ 与 $∠ B E F$ 的数量关系，并证明．

查看试题解析
27. 在平面直角坐标系 $x O y$ 中，对于任意一点 $P (x ， y)$ ，定义点P的“ $M A X$ 轴距” $Z (P)$ 为： $Z (P) = {\begin{array}{l} | x | ，当 | x | \geq | y | 时 \\ | y | ，当 | x | < | y | 时 \end{array}$ ．例如，点 $A (3 ， 5)$ ，因为 $| 5 | > | 3 |$ ，所以点A的“ $M A X$ 轴距” $Z (A) = | 5 | = 5$ ．

(1)、点 $B (\frac{1}{2} ， \frac{1}{2})$ 的“ $M A X$ 轴距” $Z (B) =$ ；点 $C (- 3 ， 2)$ 的“ $M A X$ 轴距” $Z (C) =$ ；

(2)、已知直线l经过点 $(0 ， 1)$ ，且垂直于y轴，点D在直线l上．
①若点D的“ $M A X$ 轴距” $Z (D) = 2$ ，求点D的坐标；
②请你找到一点D，使得点D的“ $M A X$ 轴距” $Z (D) = 1$ ，则D点的坐标可以是 ▲ （写出一个即可）；

(3)、已知线段 $E F ， E (- 3 ， 2) ， F (- 4 ， 0)$ ，将线段 $E F$ 向右平移 $a (a > 0)$ 个单位长度得到线段 $E^{'} F^{'}$ ，若线段 $E^{'} F^{'}$ 上恰好有两个点的“ $M A X$ 轴距”为2，请你写出满足条件的a的两个取值．

查看试题解析

x	17	17.1	17.2	17.3	17.4	17.5	17.6	17.7	17.8	17.9	18
$x^{2}$	289	292.41	295.84	299.29	302.76	306.25	309.76	313.29	316.84	320.41	324