初中数学同步训练必刷题(人教版八年级下册 18.2.3 正方形)
试卷更新日期:2023-02-22 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 下列命题中,错误的是( )A、两组对边分别相等的四边形是平行四边形 B、有一个角是直角的平行四边形是矩形 C、对角线互相垂直的四边形是菱形 D、有一组邻边相等的矩形是正方形2. 如图,已知矩形ABCD中,添加下列条件能使矩形ABCD成为正方形的是( )
 A、AC=BD B、AB⊥BC C、AD=BC D、AC⊥BD3. 如图,在平面直角坐标系中,四边形为正方形,点的坐标为(0,2),点的坐标为(4,0),则点的坐标为( )
A、AC=BD B、AB⊥BC C、AD=BC D、AC⊥BD3. 如图,在平面直角坐标系中,四边形为正方形,点的坐标为(0,2),点的坐标为(4,0),则点的坐标为( ) A、 B、 C、 D、4. 如图1,直角三角形纸片的一条直角边长为1,斜边为3.把它们按图2,拼摆正方形,纸片在结合部分不重叠无缝隙,则图2的中间空白部分,即四边形ABCD的面积为( )
A、 B、 C、 D、4. 如图1,直角三角形纸片的一条直角边长为1,斜边为3.把它们按图2,拼摆正方形,纸片在结合部分不重叠无缝隙,则图2的中间空白部分,即四边形ABCD的面积为( ) A、 B、9 C、 D、以上都不对5. 已知四边形是矩形,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )
A、 B、9 C、 D、以上都不对5. 已知四边形是矩形,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( ) A、 B、 C、 D、6. 如图,延长正方形边至点E,使 , 则为( )
A、 B、 C、 D、6. 如图,延长正方形边至点E,使 , 则为( ) A、22.5° B、25° C、30° D、45°7. 如图,三个边长相同的正方形重叠在一起,、是其中两个正方形的中心,阴影部分的面积和是4,则正方形的边长为( )
A、22.5° B、25° C、30° D、45°7. 如图,三个边长相同的正方形重叠在一起,、是其中两个正方形的中心,阴影部分的面积和是4,则正方形的边长为( ) A、2 B、4 C、8 D、8. 如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB= , 则点B到直线AE的距离是( )
A、2 B、4 C、8 D、8. 如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB= , 则点B到直线AE的距离是( ) A、 B、2 C、 D、39. 如图,在正方形ABCD外侧作等边 , 则的度数为( )
A、 B、2 C、 D、39. 如图,在正方形ABCD外侧作等边 , 则的度数为( )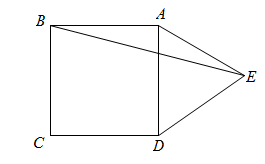 A、15° B、22.5° C、20° D、10°10. 如图,正方形的边长为1, , 是对角线,将绕点顺时针旋转45°得到 , 交于点 , 连接交于点 , 连接 , 则下列结论:①四边形是菱形;②;③;④ . 其中结论正确的是( )
A、15° B、22.5° C、20° D、10°10. 如图,正方形的边长为1, , 是对角线,将绕点顺时针旋转45°得到 , 交于点 , 连接交于点 , 连接 , 则下列结论:①四边形是菱形;②;③;④ . 其中结论正确的是( )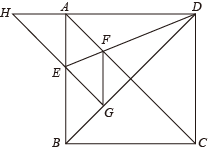 A、①②③ B、①②④ C、②③④ D、①③④
A、①②③ B、①②④ C、②③④ D、①③④二、填空题(每题3分,共24分)
-
11. 已知正方形ABCD的边长为6,如果P是正方形内一点,且 , 那么AP的长为 .12. 如图,点A在线段BG上,四边形ABCD和四边形DEFG都是正方形,面积分别是10和19,则△CDE的面积为.
 13. 如图,在正方形内作等边 , 连接 , , 则的度数为 .
13. 如图,在正方形内作等边 , 连接 , , 则的度数为 . 14. 如图,直线L经过正方形的顶点A,分别过点B、D作于点E,于点F,若 , , 则的长为 .
14. 如图,直线L经过正方形的顶点A,分别过点B、D作于点E,于点F,若 , , 则的长为 . 15. 如图,在正方形ABCD中,E为对角线BD上一点,且 ,则 的值为.
15. 如图,在正方形ABCD中,E为对角线BD上一点,且 ,则 的值为. 16. 已知矩形ABCD,请添加一个条件: , 使得矩形ABCD成为正方形.17. 如图,Rt△ABC中,四边形DBFE、GFIH都是正方形,已知AD=1cm,DB=3cm,则图中阴影部分面积为cm2.
16. 已知矩形ABCD,请添加一个条件: , 使得矩形ABCD成为正方形.17. 如图,Rt△ABC中,四边形DBFE、GFIH都是正方形,已知AD=1cm,DB=3cm,则图中阴影部分面积为cm2. 18. 如图,正方形ABCD的边长为4,点M在AB上,且 , N是BD上一动点,则的最小值为 .
18. 如图,正方形ABCD的边长为4,点M在AB上,且 , N是BD上一动点,则的最小值为 .
三、解答题(共8题,共66分)
-
19. 如图,正方形和正方形有公共点A,点B在线段上.判断与的位置关系,并说明理由;
 20. 如图,在正方形ABCD中,E,F分别是AB,AD边上的点,且AF=BE,CE,BF相交于点G,请判断线段CE与BF的关系,并说明理由.
20. 如图,在正方形ABCD中,E,F分别是AB,AD边上的点,且AF=BE,CE,BF相交于点G,请判断线段CE与BF的关系,并说明理由. 21. 已知:如图,在Rt中,平分交于点 , 垂足分别为 , 求证:四边形是正方形.
21. 已知:如图,在Rt中,平分交于点 , 垂足分别为 , 求证:四边形是正方形. 22. 如图所示,在△ABC中,∠ABC=90°,BD平分∠ABC,DE⊥BC,DF⊥AB.
22. 如图所示,在△ABC中,∠ABC=90°,BD平分∠ABC,DE⊥BC,DF⊥AB.求证:四边形BEDF是正方形.
 23. 如图,在正方形 中,点 , 在 上,且 .判断四边形 的形状,并说明理由.
23. 如图,在正方形 中,点 , 在 上,且 .判断四边形 的形状,并说明理由.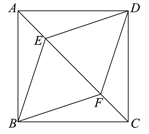 24. 如图,正方形ABCD中,E是对角线BD上一点,连接AE,CE,延长AE交CD边于点F.
24. 如图,正方形ABCD中,E是对角线BD上一点,连接AE,CE,延长AE交CD边于点F. (1)、求证: .(2)、若 , , 求证: .25. 如图,正方形的周长是40.点P是正方形对角线上一动点,过P点分别作、的垂线,垂足分别为E,F.
(1)、求证: .(2)、若 , , 求证: .25. 如图,正方形的周长是40.点P是正方形对角线上一动点,过P点分别作、的垂线,垂足分别为E,F.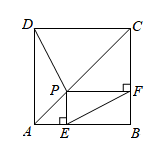 (1)、求证:四边形是矩形.(2)、请你猜想与的数量关系,并给出证明.(3)、在P点运动过程中,的长也随之变化,求的最小值.26. 如图1,在正方形中,点E是边CD上一点(点E不与点C、D重合),连接BE,过点A作交BC于点F.
(1)、求证:四边形是矩形.(2)、请你猜想与的数量关系,并给出证明.(3)、在P点运动过程中,的长也随之变化,求的最小值.26. 如图1,在正方形中,点E是边CD上一点(点E不与点C、D重合),连接BE,过点A作交BC于点F.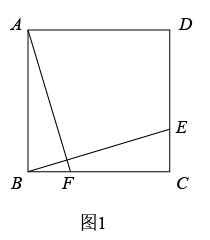

 (1)、求证:;(2)、如图2,取BE的中点M,过点M作 , 交AD于点G,交BC于点H.
(1)、求证:;(2)、如图2,取BE的中点M,过点M作 , 交AD于点G,交BC于点H.①求证:;
②连接CM,若 , 求GH的长;
(3)、如图3,取BE的中点M,连接CM,过点C作交AD于点G,连接EG、MG,若 , 则四边形的面积为 . (直接写出结果)