2023年苏科版数学八年级下册全方位训练卷第九章中心对称图形——平行四边形（进阶版）

试卷更新日期：2023-02-21 类型：单元试卷

进入出卷网下载

一、单选题（每题2分，共16分）

1. 已知点D与点 A（8，0），B（0，6），C（ a ， -a ）是一个平行四边形的四个顶点，则CD长的最小值为（）

A、8 B、 $7 \sqrt{2}$ C、 $\frac{13}{2} \sqrt{2}$ D、6

查看试题解析
2. 在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，使其与图中阴影部分构成中心对称图形．该小正方形的序号是（）

A、 $①$ B、 $②$ C、 $③$ D、 $④$

查看试题解析
3. 如图，在矩形 $A B C D$ 中， $A B = 4 ， B C = 3 ， C E = 2 B E ， E F = 2$ ，连接 $A F$ ，将线段 $A F$ 绕着点A顺时针旋转 $90 °$ 得到 $A P$ ，则线段 $P E$ 的最小值为（）

A、 $2 \sqrt{5}$ B、 $\sqrt{34} - 1$ C、4 D、 $\sqrt{34} - 2$

查看试题解析
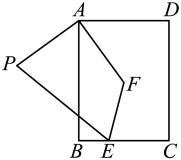4. 如图，已知点D是等边三角形ABC中BC的中点，BC＝2，点E是AC边上的动点，则BE＋ED的和最小值为（）

A、 $\sqrt{5}$ B、 $\sqrt{7}$ C、3 D、 $\sqrt{3} + 1$

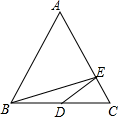查看试题解析
5. 如图，在矩形ABCD中，AB＝4，BC＝8，E为CD边的中点，P，Q为BC边上两个动点，且PQ＝2，当四边形APQE的周长最小时，BP的长为（）

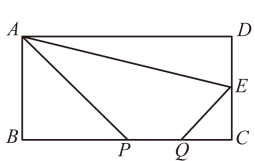A、0 B、3 C、4 D、6

查看试题解析
6. 如图所示，在菱形ABCD中，AB＝6，∠BAD＝120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．当点E、F在BC、CD上滑动时，△CEF的面积最大值是（）

A、4 $\sqrt{3}$ B、 $\frac{5}{4} \sqrt{3}$ C、3 $\sqrt{3}$ D、 $\frac{9}{4} \sqrt{3}$

查看试题解析
7. 如图，在正方形 $A B C D$ 中， $E$ 为对角线 $A C$ 上一点，连接 $D E$ ，过点 $E$ 作 $E F ⊥ D E$ ，交 $B C$ 延长线于点 $F$ ，以 $D E$ ， $E F$ 为邻边作矩形 $D E F G$ ，连接 $C G .$ 在下列结论中：
$① D E = E F$ ； $② △ D A E$ ≌ $△ D C G$ ； $③ A C ⊥ C G$ ； $④ C E = C F .$ 其中正确的是（）

A、②③④ B、①②③ C、①②④ D、①③④

查看试题解析
8. 如图，菱形ABCD中，∠BAD＝60°，AC、BD交于点O，E为CD延长线上的一点，且CD＝DE，连接BE分别交AC，AD于点F、G，连接OG、AE.则下列结论：①OG＝ $\frac{1}{2}$ AB； ②四边形ABDE是菱形；③S_四边形_ODGF＝S_△_ABF；其中正确的是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析

二、填空题（每题2分，共16分）

9. 在四边形 $A B C D$ 中，现给出下列结论：
①若 $A B = C D$ ， $A D ∥ B C$ ，则四边形 $A B C D$ 是平行四边形；
②若 $∠ A = ∠ C$ ， $∠ B = ∠ D$ ，则四边形 $A B C D$ 是平行四边形；
③若 $A B ∥ C D$ ， $∠ A = ∠ C$ ，则四边形 $A B C D$ 是平行四边形；
④若 $A B = C D$ ， $∠ A = ∠ C$ ，则四边形 $A B C D$ 是平行四边形.
其中正确的结论是.（写出所有正确结论的序号）

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ C < 90 °$ ， $∠ B = 30 °$ ， $A B = 10$ ， $A C = 7$ ， O为 $A C$ 的中点，M为 $B C$ 边上一动点，将 $△ A B C$ 绕点A逆时针旋转角 $α (0 ° < α \leq 360 °)$ 得到 $△ A B^{'} C^{'}$ ，点M的对应点为 $M^{'}$ ，连接 $O M^{'}$ ，在旋转过程中，线段 $O M^{'}$ 的长度的最小值是．

查看试题解析
11. 如图，△ABC中，∠C＝90°，AC＝6，BC＝4，点O是AC的中点，以O为旋转中心，将△ABC绕点O旋转一周，A、B、C的对应点分别为A'、B'、C'，则BC'的最大值为．

查看试题解析
12. 小明同学学习了菱形的知识后，结合之前学习的赵爽弦图，编了一个菱形版“赵爽弦图” $.$ 如图，菱形 $A B C D$ 中， $∠ A B C = 60 °$ ，四边形 $E F G H$ 是矩形，若 $F A = F B = 2 \sqrt{2}$ ，则矩形 $E F G H$ 的面积为．

查看试题解析
13. 如图，点 $E$ 、 $F$ 分别在菱形 $A B C D$ 的边 $A D$ 、 $C D$ 上， $△ E F D$ 为等边三角形， $G$ 是 $B E$ 的中点，延长 $A G$ 交 $B C$ 于点 $H$ ，已知 $A B = 6$ ，四边形 $G H C F$ 的面积是 $△ A B G$ 的面积的2倍，则 $E D$ 的长为．

查看试题解析
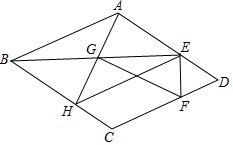14. 如图，正方形ABCD边长为2，F为对角线AC上的一个动点，过C作AC的垂线并截取 $C E = A F$ ，连结EF， $△ E C F$ 周长的最小值为．

查看试题解析
15. 如图，在▱ $A B C D$ 中， $A C$ 是对角线， $∠ A C D = 90 °$ ，点 $E$ 是 $B C$ 的中点， $A F$ 平分 $∠ B A C$ ， $C F ⊥ A F$ 于点 $F$ ，连接 $E F .$ 已知 $A B = 5$ ， $B C = 13$ ，则 $E F$ 的长为.

查看试题解析
16. 如图，定义：平面上一点到图形上所有点的最短距离，叫做这点到图形的距离.如图，P为平面上一点，正方形绕其中心O旋转，它边长为1，PO＝1，点P到正方形的距离为d，则d的取值范围是 .

查看试题解析

三、作图题（共2题，共12分）

17. 在小正方形构成的网格中，每个小正方形的顶点叫做格点．

（1） $△ A B C$ 的三个顶点都在格点上．

$①$ 在图1中，画出一个与 $△ A B C$ 成中心对称的格点三角形； $②$ 在图2中，画出 $△ A B C$ 绕着点 $C$ 按顺时针方向旋转 $90 °$ 后的三角形．
（2）如图3是由5个边长为1的小正方形拼成的图形，请用无刻度的直尺画经过点 $P$ 的一条直线，使它平分该图形的面积，保留连线的痕迹，不要求说明理由．

查看试题解析
18. 如图，在小正三角形组成的网格 $A B C D$ 中，每个小正三角形的顶点叫做格点，各顶点均在格点处的多边形称为格点多边形，按下列要求画图.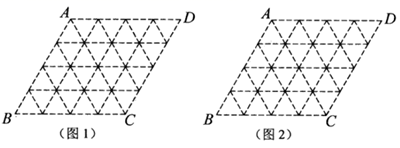

(1)、请在图1中画一个格点矩形，面积是格点四边形 $A B C D$ 面积的一半.

(2)、请在图2中画一个格点菱形，面积是格点四边形 $A B C D$ 面积的一半.

查看试题解析

四、解答题（共9题，共76分）

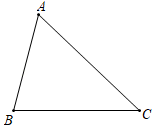
19. 证明：三角形的中位线平行于三角形的第三边，并且等于第三边的一半．
（要求：在给出的△ABC中用尺规作出AB、AC边的中点M、N ，保留作图痕迹，不要求写作法，并根据图形写出已知、求证和证明）

查看试题解析
20. 在平面直角坐标系中，已知 $O$ 为坐标原点，点 $A (1 ， 0)$ ， $B (0 ， 2)$ ．以点 $A$ 为旋转中心，把 $△ A B O$ 顺时针旋转，得 $△ A C D$ ．

(1)、如图①，当旋转后满足 $D C ∥ x$ 轴时，求点C的坐标；

(2)、如图②，当旋转后点C恰好落在x轴正半轴上时，求点D的坐标；

(3)、在（2）的条件下，边OB上的一点 $P$ 旋转后的对应点为 $P^{'}$ 当 $D P + A P^{^{'}}$ 取得最小值时，求点 $P$ 的坐标（直接写出结果即可）．

查看试题解析
21. 如图， $A B \begin{array}{l} \begin{array}{l} \begin{array}{l} ∥ \end{array} \end{array} \end{array} C D$ ，点 $E$ ， $F$ 分别在 $A B$ ， $C D$ 上，连接 $E F$ ， $∠ A E F$ 、 $∠ C F E$ 的平分线交于点 $G$ ， $∠ B E F$ 、 $∠ D F E$ 的平分线交于点 $H$ ．

(1)、求证：四边形 $E G F H$ 是矩形；

(2)、过 $G$ 作 $M N \begin{array}{l} \begin{array}{l} \begin{array}{l} ∥ \end{array} \end{array} \end{array} E F$ ，分别交 $A B$ ， $C D$ 于点 $M$ ， $N$ ，过 $H$ 作 $P Q \begin{array}{l} \begin{array}{l} \begin{array}{l} ∥ \end{array} \end{array} \end{array} E F$ ，分别交 $A B$ ， $C D$ 于点 $P$ ， $Q$ ，得到四边形 $M N Q P$ ，此时，求证四边形 $M N Q P$ 是菱形．

查看试题解析
22. 如图，四边形 $A B C D$ 是正方形，E，F是对角线 $A C$ 上的两点，且 $A E = C F$ ．

(1)、求证： $△ A D E ≌ △ C B F$ ；

(2)、求证：四边形 $B E D F$ 是菱形；

(3)、若 $A C = 8 ， A E = 2$ ，求四边形 $B E D F$ 的周长．

查看试题解析
23. 已知，如图，矩形ABCD中，AD＝3，DC＝4，菱形EFGH的三个顶点E，G，H分别在矩形ABCD的边AB，CD，DA上，AH＝1，连接CF．

(1)、当点G在边DC上运动时；探究：点F到边DC的距离FM是否为定值？如果是，请求出这个值；如果不是，请说明理由．

(2)、当DG为何值时，△FCG的面积最小，并求出这个最小值．

查看试题解析
24. 如图①，已知正方形ABCD中，E，F分别是边AD，CD上的点（点E，F不与端点重合），且AE＝DF，BE，AF交于点P，过点C作CH⊥BE交BE于点H.

(1)、求证：AF⊥BE；

(2)、若AB＝2 $\sqrt{3}$ ， AE＝2，试求线段PH的长；

(3)、如图②，连接CP并延长交AD于点Q，若点H是BP的中点，试求 $\frac{C P}{P Q}$ 的值.

查看试题解析
25. 如图

(1)、数学课上，张老师给出了一个问题：如图1，四边形ABCD是正方形，点E是边BC的中点，∠AEF＝90°，且EF交正方形外角∠DCG的平分线CF于点F．求证：AE＝EF．小明经过思考展示了一种正确的解题思路：取AB的中点H，连接HE，则可以证明AE＝EF．
请你写出证明过程．

(2)、在此基础上，小颖提出：如图2，如果把“点E是边BC的中点”改为“点E是边BC上（除B、C外）的任意一点”，其他条件不变，那么结论“AE＝EF”仍然成立，你认为小颖的观点正确吗？如果正确，请写出证明过程；如果不正确，请说明理由；

(3)、如图3，如果点E是BC的延长线上（除C点外）的任意一点，其他条件不变，结论“AE＝EF”仍然成立吗？直接写出结论，不用说明理由．

查看试题解析
26. 综合与探究：
问题情境：已知，如图1，在Rt△ABC中，∠ACB＝90°，AC＝BC＝4．点D是AC的中点，点E在BC延长线上，且∠CDE＝60°．保持△ABC不动，将△CDE从图1的位置开始，绕点C顺时针旋转α°（0＜α＜180）得到△CD'E'，D、E的对应点分别为D'、E'．

(1)、初步思考：求证：DE＝AC；

(2)、操作探究：如图2，当点 $D^{'}$ 落在DE边上时，连接AD'，判断此时四边形ACE'D'的形状，并说明理由；

(3)、拓展延伸：请从A，B两题中任选一题作答，我选择题．
A．在△CDE旋转过程中，当D'E'//BC时，请直接写出此时旋转角a的度数及B、E'两点间的距离．

B．在△CDE旋转过程中，当D'E'//AB时，延长AC交D'E'于点F，请直接写出此时旋转角α的度数及线段CF的长．

查看试题解析
27. 问题提出：

(1)、如图1，在四边形ABCD中 $∠ A B C = 90^{\circ}$ ，对角线AC⊥BD，AC＝BD，E，F，G，H分别是各边的中点，求证：四边形EFGH是正方形．
问题解决：

(2)、如图2，某市有一块四边形土地ABCD，AD＝60米，DC＝80米，∠ADC是直角，P是该四边形土地内的一点，计划在四个三角形土地△APD，△APB，△BCP，△CPD中分别种植不同的花草，为了方便种植，王师傅设计出如下方案：取四边形ABCD各边的中点E，F，G，H，然后在四边形EFGH的四条边EF，FG，GH，EH铺上人行道地砖（人行道宽度不计），铺设地砖成本为20元/米，经测量AP＝BP，CP＝DP，∠APB＝∠CPD＝90°，设计要求是四边形EFGH为正方形，请问王师傅的设计方案是否符合要求，若符合，请写出证明过程，并计算铺设地砖所需的费用；若不符合，请说明理由．

查看试题解析