2023年苏科版数学八年级下册全方位训练卷第九章 中心对称图形——平行四边形（基础版）
试卷更新日期：2023-02-21 类型：单元试卷
一、单选题（每题3分，共16分）
-
1. 在平面直角坐标系中，点A的坐标为（2，3），将点 绕原点逆时针旋转90°得到点 ，则点 的坐标为（ ）A、（－3，2） B、（3，－2） C、（3，2） D、（－2，－3）2. 如图，在 中， ，以点 为旋转中心把 按顺时针旋转一定角度，得到 点 恰好落在 上，连接 则 度数为（ ）
A、 B、 C、 D、3. 下列图案既是轴对称又是中心对称图形的有（ ）A、
B、
C、
D、
4. 能判定四边形ABCD为平行四边形的条件是 （ ）A、CB=CD，AB=AD B、 C、AB//CD，AD=BC D、AB=CD，AD=BC5. 下列说法正确的是（ ）A、两组对边分别平行的四边形是平行四边形 B、有一组邻边相等的的平行四边形是矩形 C、有一个角是直角的平行四边形是菱形 D、有一组邻边相等并且有一个角是直角的四边形是正方形6. 菱形的对角线长分别是8，6，则这个菱形的面积是（ ）A、48 B、24 C、14 D、127. 下列条件中，能使菱形 为正方形的是（ ）A、 B、 C、 D、 平分8. 如图，矩形ABCD的对角线AC，BD交于点O，点E，F分别为AO，AD的中点，若EF＝4，AB＝8，则∠ACB的度数为（ ）
A、30° B、35° C、45° D、60°二、填空题（每题3分，共16）
-
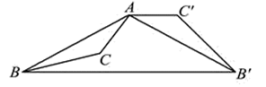
9. 如图，△ABC为钝角三角形，将△ABC绕点A按逆时针方向旋转120°得到△AB′C′，连接BB′，若AC′∥BB′，则∠C′AB′的度数为 ．
10. 在平面直角坐标系中，▱ABCD的顶点A、B、C的坐标分别是（0，2）、（﹣3，﹣4）、（2，﹣4），则顶点D的坐标是 .11. 用反证法证明：“多边形中最多有三个锐角”的第一步是：假设12. 已知矩形ABCD中，若AC=8，则BD＝ ．13. 如图，菱形ABCD的对角线AC、BD相交于点O，若AC=8，BD=6，则该菱形的周长是.
14. 如图，四边形ABCD是正方形，按如下步骤操作：①分别以点A、D为圆心，以AD长为半径画弧，两弧交于点P，连接AP、DP；②连接BP、CP，则∠PBC＝ ．
15. 如图，在▱ABCD中，对角线AC与BD相交于点O，AC⊥CD，OE∥BC交CD于E，若OC=4，CE=3，则BC的长是.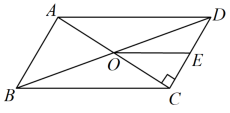
16. 如图，为估计池塘岸边 ， 两点间的距离，在池塘的一侧选取点 ， 分别取 ， 的中点 ， ， 测得 ， 则 ， 两点间的距离是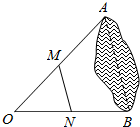
三、作图题（共9分）
-
17. 如图，在平面直角坐标系中，△ABC和△A1B1C1 关于点E成中心对称．
⑴画出对称中心E，并写出点E的坐标 ▲ ；
⑵画出△A1B1C1绕点O逆时针旋转90°后的△A2B2C2；
⑶画出与△A1B1C1关于点O成中心对称的△A3B3C3.
四、解答题（共10题，共79分）
-
18. 如图，四边形ABCD是平行四边形，点E、B、D、F在同一直线上，且BE＝DF.求证：四边形AECF是平行四边形.
19. 如图，把一张长方形（对边平行）纸条按如图所示折叠.判断三角形HBC的形状，说明理由.
20. 如图所示，点E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点，求证：四边形EFGH是平行四边形.小明同学做法是：连接BD，利用三角形的中位线定理证明得出 ， EH＝FG，从而得到四边形EFGH是平行四边形.
请你完成小明的做法：
证明：连接BD，
21. 如图，菱形ABCD的对角线相交于O点，DEAC，CEBD.
(1)、求证：四边形OCED是矩形；(2)、若AD =5，BD =8，计算DE的值.22. 如图，△ABC中，AB＝AC＝5，BC＝6．
(1)、仅用圆规在平面内找一点D（异于点A），使得点D到射线AB、AC的距离相等，且DB＝5；（不写作法，保留作图痕迹）(2)、求四边形ABDC的面积．23. 如图，正方形ABCD，E为平面内一点，且∠BEC＝90°，把△BCE绕点B逆时针旋转90°得△BAG，直线AG和直线CE交于点F.
(1)、证明：四边形BEFG是正方形；(2)、若CE＝CF，则∠AGD＝°.24. 如图，平行四边形ABCD的周长为36cm，由钝角顶点D向AB、BC引两条高DE、DF，且DE=4cm，DF=5cm.
(1)、求这个平行四边形的面积.(2)、与∠B的关系怎样？为什么？(3)、平行四边形两条对角线长分别为8cm和10cm，求则其边长x的范围.25. 如图，在平面直角坐标系中，点O为坐标原点，AB∥OC，点B，C的坐标分别为（15，8），（21，0），动点M从点A沿A→B以每秒1个单位的速度运动；动点N从点C沿C→O以每秒2个单位的速度运动．M，N同时出发，设运动时间为t秒．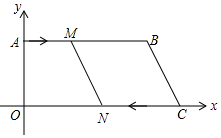
(1)、在t=3时，M点坐标 ， N点坐标 ；(2)、当t为何值时，四边形OAMN是矩形？(3)、运动过程中，四边形MNCB能否为菱形？若能，求出t的值；若不能，说明理由．26. 已知在平行四边形ABCD中，点E、F分别在AB、BC边上，DE＝AF，DE⊥AF于点G．
(1)、如图1，若∠BAD＝90°，求证：四边形ABCD是正方形；(2)、在（1）的条件下，延长CB到点H，使得BH＝AE，判断△AHF的形状，并说明理由．(3)、如图2，若AB=AD，∠AED＝60°，AE＝6，BF＝2，求DE的长．27. 定义：我们把对角线互相垂直的四边形叫做和美四边形，对角线交点称为和美四边形的中心.
(1)、写出一种你学过的和美四边形；(2)、如图1，点O是和美四边形ABCD的中心，E，F，G、H分别是边AB，BC，CD，DA的中点，连接OE，OF，OG，OH，记四边形AEOH，BEOF，CGOF，DHOG的面积为 ，用等式表示 的数量关系(无需说明理由).(3)、如图2，四边形ABCD是和美四边形，若AB=3，BC=2，CD=4，求AD的长.
-