2023年苏科版数学八年级下册全方位训练卷9.5三角形的中位线
试卷更新日期:2023-02-21 类型:同步测试
一、单选题(每题3分,共24分)
-
1. 如图,D、E、F是△ABC各边的中点,若△ABC的周长为12,则△DEF的周长为( )
 A、2 B、4 C、6 D、82. 如图,菱形ABCD的对角线AC,BD相交于点O, , , 点E为BC的中点,则OE的长为( )
A、2 B、4 C、6 D、82. 如图,菱形ABCD的对角线AC,BD相交于点O, , , 点E为BC的中点,则OE的长为( ) A、2.5 B、3 C、5 D、63. 若顺次连接四边形各边中点所得的四边形是菱形,则原四边形( )A、一定是矩形 B、一定是菱形 C、对角线一定互相垂直 D、对角线一定相等4. 如图,A、B两地被池塘隔开,小强通过下面的方法估测出A、B间的距离:先在AB外选一点C,然后步测出AC、BC的中点D、E,并且步测出DE长,由此推算出AB长.若步测DE的长为50m,则A、B间的距离是( )
A、2.5 B、3 C、5 D、63. 若顺次连接四边形各边中点所得的四边形是菱形,则原四边形( )A、一定是矩形 B、一定是菱形 C、对角线一定互相垂直 D、对角线一定相等4. 如图,A、B两地被池塘隔开,小强通过下面的方法估测出A、B间的距离:先在AB外选一点C,然后步测出AC、BC的中点D、E,并且步测出DE长,由此推算出AB长.若步测DE的长为50m,则A、B间的距离是( )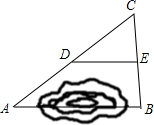 A、25m B、50m C、75m D、100m5. 如图,在四边形 中, 分别是 的中点,要使四边形 是矩形,则四边形 只需要满足一个条件是( )
A、25m B、50m C、75m D、100m5. 如图,在四边形 中, 分别是 的中点,要使四边形 是矩形,则四边形 只需要满足一个条件是( ) A、 B、 C、 D、6. 如图,在四边形ABCD中,∠A=90°,AB=3, ,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )
A、 B、 C、 D、6. 如图,在四边形ABCD中,∠A=90°,AB=3, ,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( ) A、2 B、3 C、4 D、7. 如图所示,在四边形 中,点 是对角线 的中点,点 、 分别是 、 的中点, , ,则 的度数是( )
A、2 B、3 C、4 D、7. 如图所示,在四边形 中,点 是对角线 的中点,点 、 分别是 、 的中点, , ,则 的度数是( ) A、15° B、20° C、25° D、30°8. 如图所示,吴伯伯家一块等边三角形的空地ABC,已知点E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需要篱笆的长是( )
A、15° B、20° C、25° D、30°8. 如图所示,吴伯伯家一块等边三角形的空地ABC,已知点E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需要篱笆的长是( )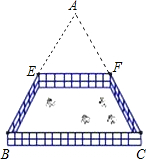 A、15米 B、20米 C、25米 D、30米
A、15米 B、20米 C、25米 D、30米二、填空题(每题3分,共24分)
-
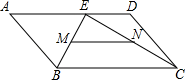
9. 如图,点E在平行四边形ABCD的边AD上,且AE=2ED,M、N分别是BE、CE的中点,连接MN,已知MN=3,则AE的长是.
 10.
10.
如图, , 分别为矩形的边 , 的中点,连接 , , .已知 , , 则的长为.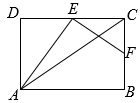 11. 中, 分别为 的中点,若 则12. 如图,在△ABC中,∠ACB=90°,AB=10 cm,BC=8cm,点D在边AB上,AD=AC,AE⊥CD,垂足为E,点F是BC的中点,则EF=cm.
11. 中, 分别为 的中点,若 则12. 如图,在△ABC中,∠ACB=90°,AB=10 cm,BC=8cm,点D在边AB上,AD=AC,AE⊥CD,垂足为E,点F是BC的中点,则EF=cm.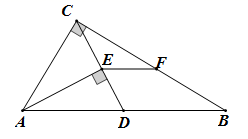 13. 如图,A,B两点被池塘隔开,不能直接测量其距离.于是小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=20m,则A,B间的距离为m.
13. 如图,A,B两点被池塘隔开,不能直接测量其距离.于是小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=20m,则A,B间的距离为m.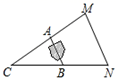 14. 如图,在平行四边形 中,对角线 、 相交于点 , , 是 边的中点, 、 为 上的点,连接 和 ,若 , , ,则图中阴影部分的面积为.
14. 如图,在平行四边形 中,对角线 、 相交于点 , , 是 边的中点, 、 为 上的点,连接 和 ,若 , , ,则图中阴影部分的面积为. 15. 在 中, , , ,点 在 边上,点 为 边上的动点,点 、 分别为 , 的中点,则 的最小值是.
15. 在 中, , , ,点 在 边上,点 为 边上的动点,点 、 分别为 , 的中点,则 的最小值是. 16. 如图,已知点 在正方形 的边 上,以 为边向正方形 外部作正方形 ,连接 , 、 分别是 、 的中点,连接 .若 , ,则 .
16. 如图,已知点 在正方形 的边 上,以 为边向正方形 外部作正方形 ,连接 , 、 分别是 、 的中点,连接 .若 , ,则 .
三、解答题(共10题,共72分)
-
17. 如图,四边形ABCD是菱形,E、F、G、H分别是边AB、BC、CD、DA的中点,连接EF、FG、GH、HE.求证:四边形EFGH是矩形.
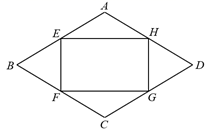 18. 如图,在平行四边形ABCD中,EF∥AB且交BC于点E,交AD于点F,连接AE、BF交于点M,连接CF、DE交于点N,连接MN.试探讨MN与AD的大小关系和位置关系,并加以证明.
18. 如图,在平行四边形ABCD中,EF∥AB且交BC于点E,交AD于点F,连接AE、BF交于点M,连接CF、DE交于点N,连接MN.试探讨MN与AD的大小关系和位置关系,并加以证明. 19. 如图,在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点且AB=CD,则EF与GH有怎样的关系?请说明你的理由.
19. 如图,在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点且AB=CD,则EF与GH有怎样的关系?请说明你的理由. 20. 如图,在中,D,E,F分别是AB,BC,CA的中点, , , 求四边形DECF的周长.
20. 如图,在中,D,E,F分别是AB,BC,CA的中点, , , 求四边形DECF的周长. 21. 如图,DE是△ABC的中位线,过点C作CF∥AB,交DE的延长线于点F.
21. 如图,DE是△ABC的中位线,过点C作CF∥AB,交DE的延长线于点F.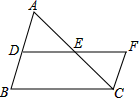 (1)、求证:BC=DF;(2)、连接CD、AF,当△ABC满足什么条件时,四边形ADCF是矩形,请说明理由.22. 如图,在中,点D,点E分别是边AC,AB的中点,点F在线段DE上,交BC于点G.
(1)、求证:BC=DF;(2)、连接CD、AF,当△ABC满足什么条件时,四边形ADCF是矩形,请说明理由.22. 如图,在中,点D,点E分别是边AC,AB的中点,点F在线段DE上,交BC于点G. (1)、证明:四边形EFGB是菱形;(2)、若 , 求DF的长度.23. 如图,在▱ABCD中,点E在边AD上,连接EB并延长至F,使BF=BE;连接EC并延长至G,使CG=CE,连接FG,点H为FG的中点,连接DH,AF.
(1)、证明:四边形EFGB是菱形;(2)、若 , 求DF的长度.23. 如图,在▱ABCD中,点E在边AD上,连接EB并延长至F,使BF=BE;连接EC并延长至G,使CG=CE,连接FG,点H为FG的中点,连接DH,AF. (1)、若∠BAE=70°,∠DCE=20°,求∠DEC的度数;(2)、求证:四边形AFHD为平行四边形.24. 如图1,在四边形 中, 、 、 、 分别是 、 、 、 的中点.
(1)、若∠BAE=70°,∠DCE=20°,求∠DEC的度数;(2)、求证:四边形AFHD为平行四边形.24. 如图1,在四边形 中, 、 、 、 分别是 、 、 、 的中点.
 (1)、求证:四边形 是平行四边形;(2)、如图2,延长 、 相交于点 ,连接 、 、 ,若 ,求四边形 的面积.25. 如图,已知四边形ABCD是正方形.
(1)、求证:四边形 是平行四边形;(2)、如图2,延长 、 相交于点 ,连接 、 、 ,若 ,求四边形 的面积.25. 如图,已知四边形ABCD是正方形. (1)、如图1,若E、F、G分别是AB、BC、CD边上的点,AF和EG交于点O.现在提供三个关系:①AF⊥EG;②AO=FO;③AF=EG.从三个关系中选择一个作为条件,一个作为结论,形成一个真命题,完成下列填空并证明:你选择的条件是 , 结论是.(只要填写序号).(2)、如图2,点E、F分别在AD、AB上,BE⊥CF,垂足为点O,连接EF、EC,M、N分别是BF、CE的中点,MN分别交BE、CF于点G、H,求证:OG=OH;(3)、如图3,AB=3cm,E为CD边上一点,∠DAE=30°,O为AE的中点,过点O的直线分别交AD、BC于点M、N,若MN=AE,请直接写出AM的长.26. 我们知道,平行四边形的对边平行且相等.利用这一性质,可以为证明线段之间的位置关系和数量关系提供帮助.(1)、重温定理,识别图形
(1)、如图1,若E、F、G分别是AB、BC、CD边上的点,AF和EG交于点O.现在提供三个关系:①AF⊥EG;②AO=FO;③AF=EG.从三个关系中选择一个作为条件,一个作为结论,形成一个真命题,完成下列填空并证明:你选择的条件是 , 结论是.(只要填写序号).(2)、如图2,点E、F分别在AD、AB上,BE⊥CF,垂足为点O,连接EF、EC,M、N分别是BF、CE的中点,MN分别交BE、CF于点G、H,求证:OG=OH;(3)、如图3,AB=3cm,E为CD边上一点,∠DAE=30°,O为AE的中点,过点O的直线分别交AD、BC于点M、N,若MN=AE,请直接写出AM的长.26. 我们知道,平行四边形的对边平行且相等.利用这一性质,可以为证明线段之间的位置关系和数量关系提供帮助.(1)、重温定理,识别图形如图①,我们在探究三角形中位线DE和第三边BC的关系时,所作的辅助线为“延长DE到点F,使EF=DE,连接CF”,此时DE与DF在同一直线上且DE= DF,又可证图中的四边形为平行四边形,可得BC与DF的关系是 , 于是推导出了“DE BC,DE= BC”.
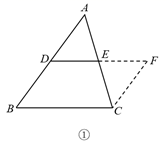 (2)、寻找图形,完成证明
(2)、寻找图形,完成证明如图②,四边形ABCD和四边形AEFG都是正方形,△BEH是等腰直角三角形,∠EBH=90°,连接CF、CH.求证CF= BE.
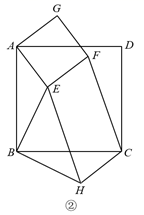 (3)、构造图形,解决问题
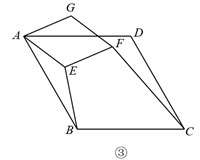
(3)、构造图形,解决问题如图③,四边形ABCD和四边形AEFG都是菱形,∠ABC=∠AEF=120°,连接BE、CF.直接写出CF与BE的数量关系.