2023年苏科版数学八年级下册全方位训练卷9.4矩形、菱形、正方形

试卷更新日期：2023-02-21 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共24分）

1. 下列命题中，是真命题的是（）

A、有一个角是直角的四边形是矩形 B、对角线相等的平行四边形是菱形 C、一组邻边相等的平行四边形是菱形 D、四边都相等的四边形是正方形

查看试题解析
2. 如图，已知四边形 $A B C D$ 是平行四边形，对角线 $A C 、 B D$ 交于点 $O$ ，则下列结论中错误的是（）

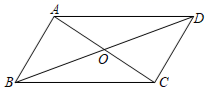A、当 $A B = B C$ 时，它是菱形 B、当 $∠ A B C = 90 °$ 时，它是正方形 C、当 $A C = B D$ 时，它是矩形 D、当 $A C ⊥ B D$ 时，它是菱形

查看试题解析
3. 下面性质中矩形具有而菱形没有的是（）

A、对角线相等 B、邻边相等 C、对角线垂直 D、对边相等

查看试题解析
4. 若菱形的两条对角线的长分别为6和10，则菱形的面积为（）

A、15 B、24 C、30 D、60

查看试题解析
5. 在矩形ABCD中，对角线AC，BD相交于点O，∠AOD=60°，OB=2cm，那么矩形ABCD的面积为（）

A、 $\sqrt{3}$ cm B、2 $\sqrt{3}$ cm C、3 $\sqrt{3}$ cm D、4 $\sqrt{3}$ cm

查看试题解析
6. 如图，若四边形ABCD是菱形，AC=24，BD=10，则菱形ABCD的边长是（）

A、13 B、12 C、26 D、52

查看试题解析
7. 如图，把正方形纸片ABCD沿对边中点所在直线折叠后展开，折痕为MN；再过点D折叠，使得点A落在MN上的点F处，折痕为DE，则 $\frac{E M}{F N}$ 的值是（）

A、 $\sqrt{3}$ B、 $\sqrt{3}$ －1 C、2－ $\sqrt{3}$ D、3－ $\sqrt{3}$

查看试题解析
8. 正方形ABCD中，对角线AC、BD交于点O，则∠CBO等于（）

A、30° B、45° C、60° D、75°

查看试题解析

二、填空题（每题3分，共24分）

9. 如图，矩形ABCD的对角线AC、BD相交于点O，∠BOC＝120°，AC＝6．则AB＝．

查看试题解析
10. 如图，过四边形ABCD的四个顶点分别作对角线AC、BD的平行线，若所围成的四边形EFGH是矩形，则原四边形ABCD需满足的条件是.（只需写出一个符合要求的条件）

查看试题解析
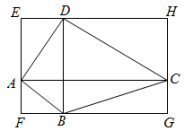11. 在矩形ABCD中，对角线AC、BD相交于点O，AO＝6cm，则BD＝cm．

查看试题解析
12. 菱形的两条对角线长分别是 $16 cm$ 和 $12 cm$ ，则菱形的周长是 $cm$ .

查看试题解析
13. 已知一个菱形的边长为 $5$ ，其中一条对角线长为 $8$ ，则这个菱形的面积为.

查看试题解析
14. 如图，正方形 $A B C D$ 在第一象限，点 $A (a ， b)$ 、 $C (c ， b)$ ，则点 $B$ 的坐标是．（用含 $a$ 、 $b$ 、 $c$ 的代数式表示）

查看试题解析
15. 如图，正方形 $A B C D$ 和正方形 $C E F G$ 的边长分别为4和2，正方形 $C E F G$ 绕点C旋转，则 $D E^{2} + B G^{2} =$ ．

查看试题解析
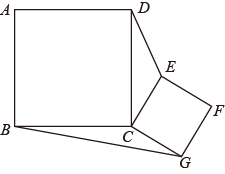16. 如图，木制活动衣帽架由三个全等的菱形构成，在 $A$ ， $E$ ， $F$ ， $C$ ， $G$ ， $H$ 处安装上、下两排挂钩，可以根据需要改变挂钩间的距离，并在 $B$ ， $M$ 处固定.已知菱形 $A B C D$ 的边长为13cm，要使两排挂钩间的距离 $A C$ 为24cm，则 $B$ ， $D$ 之间的距离（即线段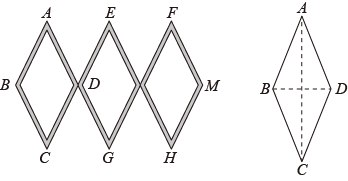 $B D$ 的长）为cm.

查看试题解析

三、作图题（共10分）

17. 如图1、2都是边长为1的全等菱形组成的网格图，网格的交点称为格点，AB是端点落在格点上的线段，请仅用无刻度直尺作出符合下列要求的格点四边形．

(1)、请在图1中作出一个以AB为边的平行四边形（非矩形）．

(2)、请在图2中作出一个以AB为边的矩形．

查看试题解析

四、解答题（共8题，共62分）

18. 已知：如图，在正方形ABCD中，点P是对角线BD上一点，PM⊥AD，PN⊥AB，垂足分别为M、N.求证：MN=PC.

查看试题解析
19. 如图，菱形ABCD的对角线AC、BD相交于点O， $B E // A C$ ， $A E // B D$ ，OE与AB交于点F.

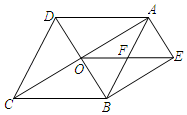(1)、求证：四边形AEBO为矩形；

(2)、若OE＝10，AC＝16，求菱形ABCD的面积.

查看试题解析
20. 如图，已知菱形ABCD的对角线相交于点O，延长AB至点E，使BE＝AB，连接CE．

(1)、求证：BD＝EC；

(2)、当∠DAB为多少度时，四边形BECD为菱形？并说明理由．

查看试题解析
21. 操作：第一步：如图1，对折长方形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开.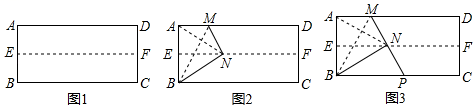
第二步：如图2，再一次折叠纸片，使点A落在EF上的N处，并使折痕经过点B，得到折痕BM，同时得到线段BN.连结AN，易知△ABN的形状是 ▲ .
论证：如图3，若延长MN交BC于点P，试判定△BMP的形状，请说明理由.

查看试题解析
22. 如图，平行四边形 $A B C D$ 中， $A B ⊥ A C$ ， $A C = 2 A B$ .对角线 $A C$ ， $B D$ 相交于点 $O$ ，将直线 $A C$ 绕点 $O$ 顺时针旋转 $β ° (0 < β < 180)$ ，分别交直线 $B C$ 、 $A D$ 于点 $E$ 、 $F$ .

(1)、当 $β =$ °，四边形 $A B E F$ 是平行四边形；

(2)、在旋转的过程中，从 $A$ 、 $B$ 、 $C$ 、 $D$ 、 $E$ 、 $F$ 中任意找4个点为顶点构造四边形.
① $β =$ ▲ °，构造的四边形是菱形；

②若构造的四边形是矩形，则不同的矩形应该有 ▲ 个.

查看试题解析
23. 如图1，在边长为4的正方形ABCD中，点E为对角线BD上一点，连接AE，过点E作 $E F ⊥ A E$ ，交边CD于点F，若 $D F = 2$ ，求BE的长.
下面是小明、小华和小东三位同学关于本题不同视角下的部分思维过程：

小明：从直线BD是正方形的对称轴角度看，连接EC，如图2，则 $E A = E C$ ， ∠ECD＝∠EAD，又 $∠ A D C = ∠ A E F = 9 0^{∘}$ ， ……

小华：从 $E F ⊥ A E$ 的角度看，可以过点E作BC的平行线，交AB、CD于M、N，如图3，通过证明 $△ A M E ≅ △ E N F$ ， ……

小东：从 $E F ⊥ A E$ 的角度看，还可以过点E作BD的垂线，交DC的延长线于点P，如图4，……

请结合上面的思路，求BE的长.

查看试题解析
24. 问题情境：
如图①，点E为正方形ABCD内一点，∠AEB＝90°，将Rt△ABE绕点B按顺时针方向旋转90°，得到△CBE′（点A的对应点为点C）．延长AE交CE′于点F，连接DE．

(1)、猜想证明：
试判断四边形BE'FE的形状，并说明理由；

(2)、如图②，若DA＝DE，请猜想线段CF与 $F E^{'}$ 的数量关系并加以证明；

(3)、解决问题：
如图①，若AB＝4，当BE的长为时，△ADE为等腰三角形，请直接写出结果．

查看试题解析
25.

(1)、【方法回顾】
如图1，过正方形ABCD的顶点A作一条直线l交边BC于点P，BE⊥AP于点E，DF⊥AP于点F，若DF＝2.5，BE＝1，则EF＝．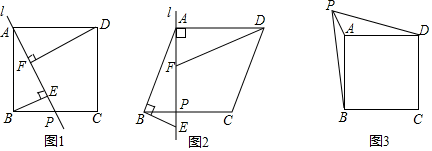

(2)、【问题解决】
如图2，菱形ABCD的边长为1.5，过点A作一条直线l交边BC于点P，且∠DAP＝90°，点F是AP上一点，且∠BAD+∠AFD＝180°，过点B作BE⊥AB，与直线l交于点E，若EF＝1，求BE的长．

(3)、【思维拓展】
如图3，在正方形ABCD中，点P在AD所在直线上的上方，AP＝2，连接PB，PD，若△PAD的面积与△PAB的面积之差为m（m＞0），则PB²﹣PD²的值为．（用含m的式子表示）

查看试题解析