2023年苏科版数学八年级下册全方位训练卷9.3平行四边形
试卷更新日期:2023-02-21 类型:同步测试
一、单选题(每题3分,共24分)
-
1. 平行四边形的对角线长为x,y,一边长为14,则x,y的值可能是( )A、8和16 B、10和14 C、18和10 D、10和242. 如图,在平行四边形ABCD中,AB=5,BC=8,∠ABC和∠BCD的角平分线分别交AD于点E和F,若BE=6,则CF=( )
 A、6 B、8 C、10 D、133. 如图,点A在平行四边形的对角线上,试判断S1 , S2之间的大小关系( )
A、6 B、8 C、10 D、133. 如图,点A在平行四边形的对角线上,试判断S1 , S2之间的大小关系( ) A、S1=S2 B、S1>S2 C、S1<S2 D、无法确定4. 如图,点P为▱ABCD外一点,连接PA、PB、PC、PD,若△APB的面积为18,△APD的面积为5,则△APC的面积为( )
A、S1=S2 B、S1>S2 C、S1<S2 D、无法确定4. 如图,点P为▱ABCD外一点,连接PA、PB、PC、PD,若△APB的面积为18,△APD的面积为5,则△APC的面积为( )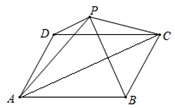 A、10 B、13 C、18 D、205. 下列条件中,能判定四边形是平行四边形的条件是( )A、一组对边平行,另一组对边相等 B、一组对边平行,一组对角相等 C、一组对边平行,一组邻角互补 D、一组对边相等,一组邻角相等6. 下列条件中,不能确定四边形ABCD为平行四边形的是( )A、∠A=∠C,∠B=∠D B、∠A+∠B=180°,∠B+∠C=180° C、 ,AD=BC D、 ,AD=BC7. 如图,△ABC是等边三角形,P是三角形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为24,则PD+PE+PF=( )
A、10 B、13 C、18 D、205. 下列条件中,能判定四边形是平行四边形的条件是( )A、一组对边平行,另一组对边相等 B、一组对边平行,一组对角相等 C、一组对边平行,一组邻角互补 D、一组对边相等,一组邻角相等6. 下列条件中,不能确定四边形ABCD为平行四边形的是( )A、∠A=∠C,∠B=∠D B、∠A+∠B=180°,∠B+∠C=180° C、 ,AD=BC D、 ,AD=BC7. 如图,△ABC是等边三角形,P是三角形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为24,则PD+PE+PF=( ) A、8 B、9 C、12 D、158. 若用反证法证明命题“四边形中至少有一个角是钝角或直角”时,则首先应该假设这个四边形中( )A、至少有一个角是钝角或直角 B、没有一个角是锐角 C、没有一个角是钝角或直角 D、每一个角都是钝角或直角
A、8 B、9 C、12 D、158. 若用反证法证明命题“四边形中至少有一个角是钝角或直角”时,则首先应该假设这个四边形中( )A、至少有一个角是钝角或直角 B、没有一个角是锐角 C、没有一个角是钝角或直角 D、每一个角都是钝角或直角二、填空题(每空3分,共21分)
-
9. 用反证法证明某一命题的结论“ ”时,应假设.10. 平行四边形ABCD中,∠A:∠B=2:7,则∠C=°11. 如图,在平行四边形 ABCD中,AD=7,AB=5,DE平分∠ADC交BC于点E,则BE的长是 .
 12. 如图,在中,点是定点,点、是直线和上两动点, , 且点到直线和的距离分别是1和4,则对角线长度的最小值是 .
12. 如图,在中,点是定点,点、是直线和上两动点, , 且点到直线和的距离分别是1和4,则对角线长度的最小值是 . 13. 如图,平行四边形ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,连接AP,若S△PBG=2,则S四边形AEPH=.
13. 如图,平行四边形ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,连接AP,若S△PBG=2,则S四边形AEPH=. 14. 如图,在平行四边形ABCD中,对角线交于点0,点E、F在直线AC上(不同于A、C),当E、F的位置满足的条件时,四边形DEBF是平行四边形.
14. 如图,在平行四边形ABCD中,对角线交于点0,点E、F在直线AC上(不同于A、C),当E、F的位置满足的条件时,四边形DEBF是平行四边形.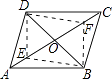 15. 如图,在四边形 中, ,点 分别从点 同时出发,点 以 的速度由点 向点 运动,点 以 的速度由点 向点 运动设运动时间为 .当 .时, 为平行四边形的一边.
15. 如图,在四边形 中, ,点 分别从点 同时出发,点 以 的速度由点 向点 运动,点 以 的速度由点 向点 运动设运动时间为 .当 .时, 为平行四边形的一边.
三、作图题(共2题,共14分)
-
16. 按下列要求画 ,使它的四个顶点以及对角线交点都在方格的顶点上,
 (1)、在图①中画 ,使它的周长是整数;(2)、在图②中画 ,使它的周长不是整数(请标出必要的字母与线段长度)17. 题目:
(1)、在图①中画 ,使它的周长是整数;(2)、在图②中画 ,使它的周长不是整数(请标出必要的字母与线段长度)17. 题目: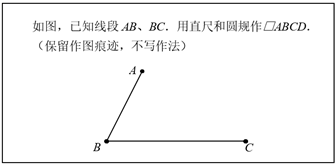 (1)、下图是小明所作的图,根据作图痕迹,可以知道他作图的依据是“的四边形是平行四边形”;
(1)、下图是小明所作的图,根据作图痕迹,可以知道他作图的依据是“的四边形是平行四边形”;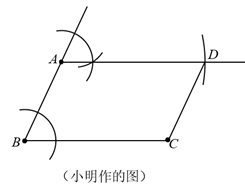 (2)、请你以“对角线互相平分的四边形是平行四边形”为依据完成题目中的作图.
(2)、请你以“对角线互相平分的四边形是平行四边形”为依据完成题目中的作图.四、解答题(共9题,共61分)
-
18. 证明此命题为伪命题:一组对边相等且一组对角相等的四边形是平行四边形.19. 如图,E、F是平行四边形ABCD对角线BD上的两点,且BE=DF.求证:四边形AECF是平行四边形.
 20. 平行四边形ABCD中,对角线AC与BD相交于O,E、F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.21. 平行四边形的一个判定定理是:对角线互相平分的四边形是平行四边形.请你证明这个判定定理.
20. 平行四边形ABCD中,对角线AC与BD相交于O,E、F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.21. 平行四边形的一个判定定理是:对角线互相平分的四边形是平行四边形.请你证明这个判定定理.已知:如图,在四边形ABCD中,AC,BD相交于点O,OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
证明:
 22. 如图是某区部分街道示意图,其中 垂直平分 .从 站乘车到 站只有两条路线有直接到达的公交车,路线1是 ,且长度为5公里,路线2是 ,求路线2的长度.
22. 如图是某区部分街道示意图,其中 垂直平分 .从 站乘车到 站只有两条路线有直接到达的公交车,路线1是 ,且长度为5公里,路线2是 ,求路线2的长度. 23. 已知:如图,E、F是▱ABCD的对角线AC上的两点,AE=CF.
23. 已知:如图,E、F是▱ABCD的对角线AC上的两点,AE=CF.求证:
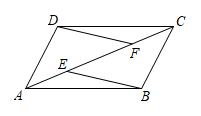 (1)、△ADF≌△CBE;(2)、EB∥DF.24. 如图,平行四边形ABCD的对角线AC,BD相交于О点,于E点,于F.
(1)、△ADF≌△CBE;(2)、EB∥DF.24. 如图,平行四边形ABCD的对角线AC,BD相交于О点,于E点,于F. (1)、求证:四边形DEBF为平行四边形;(2)、若 , , , 求的面积.25. 定义:有三个角相等的四边形叫做三等角四边形.
(1)、求证:四边形DEBF为平行四边形;(2)、若 , , , 求的面积.25. 定义:有三个角相等的四边形叫做三等角四边形.
 (1)、在三等角四边形 中, ,则 的取值范围为;(2)、如图1,折叠平行四边形 ,使得顶点 分别落在边 上的点 处,折痕为 .求证:四边形 为三等角四边形;(3)、如图 ,在三等角四边形 中, ,若 , , ,则 的长度为.26. 【教材呈现】下图是华师版八年级下册数学教材第77页的部分内容.
(1)、在三等角四边形 中, ,则 的取值范围为;(2)、如图1,折叠平行四边形 ,使得顶点 分别落在边 上的点 处,折痕为 .求证:四边形 为三等角四边形;(3)、如图 ,在三等角四边形 中, ,若 , , ,则 的长度为.26. 【教材呈现】下图是华师版八年级下册数学教材第77页的部分内容.平行四边形的性质定理3:行四边形的对角线互相平分。
我们可以用演绎推理证明这个结论。
已知:如图,的对角线AC和BD相交于点O。
求证:OA=OC,OB=OD。
 (1)、请根据教材中的分析,结合图1写出“平行四边形的对角线互相平分”这一性质的完整的证明过程.
(1)、请根据教材中的分析,结合图1写出“平行四边形的对角线互相平分”这一性质的完整的证明过程.证明:
 (2)、【性质应用】
(2)、【性质应用】如图2,的对角线相交于点 , 过点且与分别相交于点 ,
求证:;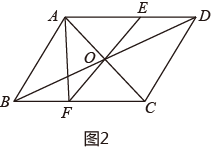 (3)、连结 , 若 , 周长是 , 则的周长是.
(3)、连结 , 若 , 周长是 , 则的周长是.