2023年苏科版数学八年级下册全方位训练卷9.1图形的旋转
试卷更新日期:2023-02-21 类型:同步测试
一、单选题(每题3分,共24分)
-
1. 如图,在新型俄罗斯方块游戏中(出现的图案可进行顺时针、逆时针旋转;向左、向右平移),已拼好的图案如图3所示,现又出现一个形如“
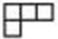 ”的方块正向下运动,你必须进行以下哪项操作,才能拼成一个完整的图形( ).
”的方块正向下运动,你必须进行以下哪项操作,才能拼成一个完整的图形( ).  A、顺时针旋转90°,向右平移 B、逆时针旋转90°,向右平移 C、顺时针旋转90°,向左平移 D、逆时针旋转90°,向左平移2. 将图中可爱的“小鸭子”图片按逆时针方向旋转90°后得到的图片是( )
A、顺时针旋转90°,向右平移 B、逆时针旋转90°,向右平移 C、顺时针旋转90°,向左平移 D、逆时针旋转90°,向左平移2. 将图中可爱的“小鸭子”图片按逆时针方向旋转90°后得到的图片是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 如图,将绕着点O顺时针旋转,得到(点C落在外),若 , , 则最小旋转角度是( )
3. 如图,将绕着点O顺时针旋转,得到(点C落在外),若 , , 则最小旋转角度是( ) A、20° B、30° C、40° D、50°4. 如图,若正方形ABCD绕图中某点顺时针旋转90°得到正方形EFGH,则旋转中心应是( )
A、20° B、30° C、40° D、50°4. 如图,若正方形ABCD绕图中某点顺时针旋转90°得到正方形EFGH,则旋转中心应是( )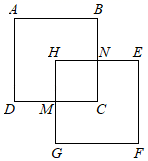 A、H点 B、N点 C、C点 D、M点5. 将如图所示的图形绕中心按顺时针方向旋转60°后可得到的图形是( )
A、H点 B、N点 C、C点 D、M点5. 将如图所示的图形绕中心按顺时针方向旋转60°后可得到的图形是( )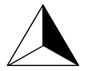 A、
A、 B、
B、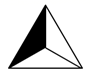 C、
C、 D、
D、 6. 以如图的右边缘所在直线为轴将该图案向右翻折后,再绕正方形的中心旋转 , 所得到的图形是
6. 以如图的右边缘所在直线为轴将该图案向右翻折后,再绕正方形的中心旋转 , 所得到的图形是 A、
A、 B、
B、 C、
C、 D、
D、 7. 如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC,若AB=10,BC=6.则线段BE的长为( )
7. 如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC,若AB=10,BC=6.则线段BE的长为( ) A、10 B、12 C、14 D、168. 如图,将绕点A按逆时针方向旋转110°得到 , 连接 , 若 , 则的度数为( )
A、10 B、12 C、14 D、168. 如图,将绕点A按逆时针方向旋转110°得到 , 连接 , 若 , 则的度数为( ) A、75° B、80° C、85° D、90°
A、75° B、80° C、85° D、90°二、填空题(每空3分,共27分)
-
9. 如图,在中, , 将绕点按逆时针方向旋转后得到 , 则阴影部分面积为 .
 10. 如图,在中, , 将绕点C按顺时针方向旋转得到 , 斜边DE交AC边于点F,当点D落在AB边上时,CF的长为 .
10. 如图,在中, , 将绕点C按顺时针方向旋转得到 , 斜边DE交AC边于点F,当点D落在AB边上时,CF的长为 . 11. 如图,将的直角三角尺绕直角顶点A逆时针旋转到的位置,使B点对应点D落在边上,连接、 , 则下列结论:①;②为的垂直平分线;③平分;④其中正确的是 .
11. 如图,将的直角三角尺绕直角顶点A逆时针旋转到的位置,使B点对应点D落在边上,连接、 , 则下列结论:①;②为的垂直平分线;③平分;④其中正确的是 . 12. 如图,一个小孩坐在秋千上,秋千绕点O旋转了86°,小孩的位置也从A点运动到了点,则度.
12. 如图,一个小孩坐在秋千上,秋千绕点O旋转了86°,小孩的位置也从A点运动到了点,则度. 13. 如图,网格中每个小正方形的边长均为1个单位长度,点A,B都在格点上.线段AB绕着某一定点顺时针旋转一个角度后,得到线段A'B'(点A',B'分别是A,B的对应点),则α的大小是.
13. 如图,网格中每个小正方形的边长均为1个单位长度,点A,B都在格点上.线段AB绕着某一定点顺时针旋转一个角度后,得到线段A'B'(点A',B'分别是A,B的对应点),则α的大小是. 14. 把一个图案进行旋转变换,选择不同的旋转中心、不同的,会有不同的效果.
14. 把一个图案进行旋转变换,选择不同的旋转中心、不同的,会有不同的效果.
15. 要使正十二边形旋转后与自身重合,至少应将它绕中心旋转的度数为16. 如图,在平面直角坐标系中,有一边长为1的正方形 , 点B在x轴的正半轴上,如果以对角线为边作第二个正方形 , 再以对角线为边作第三个正方形 , …,照此规律作下去,则的坐标是;的坐标是 .
三、作图题(共3题,共24分)
-
17. 如图所示,的顶点在的网格中的格点上.
 (1)、画出绕点A顺时针旋转90°得到的;(2)、画出绕点A逆时针旋转180°得到的 .18. 如图,在 的正方格中,中心点为点 ,图中有4个小正方格被涂黑成“ 形”.
(1)、画出绕点A顺时针旋转90°得到的;(2)、画出绕点A逆时针旋转180°得到的 .18. 如图,在 的正方格中,中心点为点 ,图中有4个小正方格被涂黑成“ 形”. (1)、用 铅笔在图中再涂黑4格,使新涂黑的图形与原来的“ 形”关于点 成中心对称;(2)、用 铅笔在图中再涂黑4格,使新涂黑的图形与原来的“ 形”所组成的新图形既是轴对称图形、又是中心对称图形 (要求画出三种 ) .19. 在平面直角坐标系xOy中, 的顶点坐标分别是 , , .
(1)、用 铅笔在图中再涂黑4格,使新涂黑的图形与原来的“ 形”关于点 成中心对称;(2)、用 铅笔在图中再涂黑4格,使新涂黑的图形与原来的“ 形”所组成的新图形既是轴对称图形、又是中心对称图形 (要求画出三种 ) .19. 在平面直角坐标系xOy中, 的顶点坐标分别是 , , . (1)、按要求画出图形:
(1)、按要求画出图形:①将 向右平移6个单位得到 ;
②再将 绕点 顺时针旋转90°得到 ;
(2)、如果将(1)中得到的 看成是由 经过以某一点M为旋转中心旋转一次得到的,请写出M的坐标.四、解答题(共7题,共45分)
-
20. 如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,求BD的长.
 21. 如图,逆时针旋转一定角度后与重合,且点在上.若 , , 求出旋转角的度数,并写出旋转中心.
21. 如图,逆时针旋转一定角度后与重合,且点在上.若 , , 求出旋转角的度数,并写出旋转中心. 22. 如图,点D在等边三角形ABC的边BC上,将△ABD绕点A旋转,使得旋转后点B的对应点为点C.小明是这样做的:如图,过点C画BA的平行线l,在l上取 , 连接AE,则△ACE即为旋转后的图形.你能说明小明这样做的道理吗?
22. 如图,点D在等边三角形ABC的边BC上,将△ABD绕点A旋转,使得旋转后点B的对应点为点C.小明是这样做的:如图,过点C画BA的平行线l,在l上取 , 连接AE,则△ACE即为旋转后的图形.你能说明小明这样做的道理吗? 23. 如图,在 中, , 平分 交 于点 ,将 绕点 逆时针旋转到 的位置,点 在 上,连接 交 于点 .求证: 垂直平分 .
23. 如图,在 中, , 平分 交 于点 ,将 绕点 逆时针旋转到 的位置,点 在 上,连接 交 于点 .求证: 垂直平分 . 24. 如图,已知△ABC是等边三角形,在△ABC外有一点D,连接AD,BD,CD,将△ACD绕点A按顺时针方向旋转得到△ABE,AD与BE交于点F, .
24. 如图,已知△ABC是等边三角形,在△ABC外有一点D,连接AD,BD,CD,将△ACD绕点A按顺时针方向旋转得到△ABE,AD与BE交于点F, .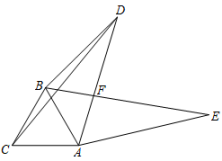 (1)、求的大小;(2)、连接DE,若BD=3,CD=5,求AD的长.25. 数学探究课上老师出了这样一道题:“如图,等边 中有一点 ,且 , , ,试求 的度数.”小明和小军探讨时发现了一种求 度数的方法,下面是这种方法的一部分思路,请按照下列思路要求画图或判断.
(1)、求的大小;(2)、连接DE,若BD=3,CD=5,求AD的长.25. 数学探究课上老师出了这样一道题:“如图,等边 中有一点 ,且 , , ,试求 的度数.”小明和小军探讨时发现了一种求 度数的方法,下面是这种方法的一部分思路,请按照下列思路要求画图或判断.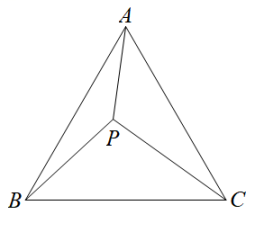 (1)、在图中画出 绕点 顺时旋转60°后的 ,并判断 的形状是 ;(2)、试判断 的形状,并说明理由;(3)、由(1)、(2)两问可知: .26. 如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)、在图中画出 绕点 顺时旋转60°后的 ,并判断 的形状是 ;(2)、试判断 的形状,并说明理由;(3)、由(1)、(2)两问可知: .26. 如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.

 (1)、操作发现如图2,固定△ABC,使△DEC绕点C旋转.当点D恰好落在BC边上时,填空:
(1)、操作发现如图2,固定△ABC,使△DEC绕点C旋转.当点D恰好落在BC边上时,填空:
①线段DE与AC的位置关系是;②设△BDC的面积为S1 , △AEC的面积为S2 . 则S1与S2的数量关系是 .
(2)、猜想论证当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想.