初中数学同步训练必刷题（人教版八年级下册 18.2.1 矩形）

试卷更新日期：2023-02-21 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 矩形具有而一般平行四边形不具有的性质是（）

A、两组对边分别相等 B、两组对角分别相等 C、两条对角线互相平分 D、两条对角线相等

查看试题解析
2. 若矩形 $A B C D$ 的邻边长分别是1，2，则 $B D$ 的长是（）

A、 $\sqrt{3}$ B、3 C、 $\sqrt{5}$ D、 $2 \sqrt{5}$

查看试题解析
3. 在矩形 $A B C D$ 中， $A B = 6 ， B C = 8$ ，对角线交于点O，则 $B O =$ （）

A、3 B、4 C、5 D、10

查看试题解析
4. 如图，在矩形 $A B C D$ 中， $A B = 1 ， A D = 2$ ，点M在边 $B C$ 上，若 $M A$ 平分 $∠ D M B$ ，则 $C M$ 的长是（）

A、 $3 \sqrt{2}$ B、 $2 \sqrt{6}$ C、 $2 \sqrt{5}$ D、 $\sqrt{3}$

查看试题解析
5. 如图所示， $O$ 是矩形 $A B C D$ 的对角线 $A C$ 的中点， $E$ 为 $A D$ 的中点．若 $A B = 6$ ， $B C = 8$ ，则 $△ B O E$ 的周长为（）

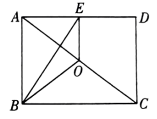A、10 B、 $8 + 2 \sqrt{5}$ C、 $8 + 2 \sqrt{13}$ D、14

查看试题解析
6. 如图，矩形ABCD中，∠BOC＝120°，BD＝12，点P是AD边上一动点，则OP的最小值为（）

A、3 B、4 C、5 D、6

查看试题解析
7. 如图，矩形 $A B C D$ 中 $A B = 8$ 把矩形沿直线 $A C$ 折叠，点 $B$ 落在点 $E$ 处， $A E$ 交 $C D$ 于点 $F$ ．若 $A F = \frac{25}{4}$ ，则 $A D$ 的长为（）

A、4 B、5 C、6 D、7

查看试题解析
8. 如图所示，点 $O$ 是矩形 $A B C D$ 对角线 $A C$ 的中点， $O E ∥ A B$ 交 $A D$ 于点 $E$ ，若 $A B = 6 ， B C = 8$ ，则 $△ B O E$ 的周长为（）

A、10 B、 $8 + 2 \sqrt{5}$ C、 $8 + 2 \sqrt{13}$ D、14

查看试题解析
9. 在 $R t △ A B C$ 中，点 $D$ 是斜边 $B C$ 上的中点，连接 $A D$ ．若 $∠ C = 68 °$ ，则 $∠ C A D =$ （）．

A、22° B、68° C、96° D、112°

查看试题解析
10. 如图，在矩形 $A B C D$ 中，点E是 $A D$ 的中点， $∠ E B C$ 的平分线交 $C D$ 于点F将 $△ D E F$ 沿 $E F$ 折叠，点D恰好落在 $E B$ 上M点处，延长 $B C 、 E F$ 交于点N，有下列四个结论：① $B F$ 垂直平分 $E N$ ；② $△ B E N$ 是等边三角形；③ $△ D E F ∽ △ F E B$ ；④ $S_{△ B E F} = 3 S_{△ D E F}$ ．其中，正确结论的序号是（）

A、①②③ B、①③④ C、②③④ D、①②④

查看试题解析

二、填空题(每题3分，共24分）

11. 一个木匠要制作矩形的踏板．他在一个对边平行的长木板上分别沿与长边垂直的方向锯两次，就能得到矩形踏板．理由是．

查看试题解析
12. 如图，O是矩形ABCD对角线AC的中点，E是AB上的一点，将 $△ B C E$ 沿CE折叠后，点B恰好与点O重合．若 $B C = 3$ ，则折痕CE的长为．

查看试题解析
13. 已知在 $△ A B C$ 中， $A C = 6 c m$ ，点D、E分别是AC、BC的中点，连接DE，在DE上有一点F， $E F = 1 c m$ ，连接AF，CF，若 $A F ⊥ C F$ ，则AB＝．

查看试题解析
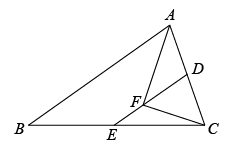14. 如图，矩形ABCD的对角线AC与BD交于点O，过点O作 $O E ⊥ A C$ ，交AD于点E，过点E作 $E F ⊥ B D$ ，垂足为F， $E F = 1$ ， $O E = 2$ ， $B D = 4 \sqrt{3}$ ，则矩形ABCD的面积为．

查看试题解析
15. 如图，在 $△$ ABC中，D，E分别是AB，AC的中点，点F，G在边BC 上，且DF $∥$ EG．只需添加一个条件即可证明四边形DFGE是矩形，这个条件可以是．（写出一个即可）

查看试题解析
16. 如图，CD，BE是 $△ A B C$ 的高，点P是BC边的中点，连接DP，EP，若 $D P = 3$ ，则EP的长是．

查看试题解析
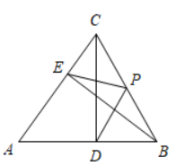17. 如图，在矩形ABCD中， $A B = 4 c m$ ， $A D = 12 c m$ ，点P从点A向点D以每秒1cm的速度运动，Q以每秒4cm的速度从点C出发，在B、C两点之间做往返运动，两点同时出发，点P到达点D为止(同时点Q也停止)，这段时间内，当运动时间为时，P、Q、C、D四点组成矩形．

查看试题解析
18. 如图，Rt△ABC中，∠BAC=90°，AB=4，AC=3，D为BC边上一点，DE⊥AB，DF⊥AC垂足分别是E，F，连接EF，则EF最小值为．

查看试题解析

三、解答题（共8题，共66分）

19. 如图， $R t △ A B C$ 中， $∠ B = 90 ° ， A B = 12 ， B C = 16 ， C D = 21 ， A D = 29$ ，点E是 $A D$ 的中点，求 $C E$ 的长．

查看试题解析
20. 如图，在△ABC中，AB＝AC，AD⊥BC于点D，过点B作AD的平行线交外角∠BAF的平分线于点E．求证：四边形ADBE是矩形．

查看试题解析
21. 如图，在矩形 $A B C D$ 中，点E是 $A B$ 的中点， $E F ⊥ A B$ 交 $C D$ 于点F，点M在 $A D$ 上，连接 $B M$ ，把 $△ A B M$ 延 $B M$ 翻折．当点A的对应点 $A^{'}$ 恰好落在 $E F$ 上时，求 $∠ C B A^{'}$ 的度数．

查看试题解析
22. 如图，四边形ABCD的对角线AC⊥BD，垂足为O，点E，F，G，H分别是AB，BC，CD，DA的中点．求证：四边形EFGH是矩形．

查看试题解析
23. 如图， $D E$ ， $D F$ 是 $△ A B C$ 的中位线， $∠ A C B = 90 °$ ，连接 $C D$ ， $E F$ ，求证： $C D = E F$ ．

查看试题解析
24. 如图， $▱ A B C D$ 的对角线相较于点O，△OAB是等边三角形，AB＝4．

(1)、求证： $▱ A B C D$ 是矩形；

(2)、求AD的长．

查看试题解析
25. 如图，在矩形ABCD中，E是AD的中点，将△ABE沿BE折叠，点A的对应点为点G.

(1)、填空：如图1，当点G恰好在BC边上时，四边形ABGE的形状是形；

(2)、如图2，当点G在矩形ABCD内部时，延长BG交DC边于点F.
求证：BF=AB+DF；

若AD= $\sqrt{3}$ AB，试探索线段DF与FC的数量关系.

查看试题解析
26. 如图①，将一张矩形纸片ABCD沿着对角线BD向上折叠，顶点C落到点E处，BE交AD于点F．

(1)、求证：△BDF是等腰三角形．

(2)、如图②，过点D作DG//BE，交BC于点G，连接FG交BD于点O．
①判断四边形BFDG的形状，并说明理由；
②若AB＝6，AD＝8，求FG的长．

查看试题解析