初中数学同步训练必刷题(人教版八年级下册 18.1.2 平行四边形的判定)
试卷更新日期:2023-02-21 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 下面各条件中,能判定四边形是平行四边形的是( )A、对角线互相垂直 B、对角线互相平分 C、一组对角相等 D、一组对边相等2. 如图,四边形的对角线交于点O,下列哪组条件能判断四边形是平行四边形( )
 A、 , B、 , C、 , D、 ,3. 在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1),为顶点构造平行四边形,下列各点中不能作为平行四边形第四个顶点的坐标的是( )
A、 , B、 , C、 , D、 ,3. 在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1),为顶点构造平行四边形,下列各点中不能作为平行四边形第四个顶点的坐标的是( )
 A、 B、 C、 D、4. 已知三角形的两边长分别为6 cm和8 cm,则下列长度的四条线段中能作为第三边上的中线是( )A、1cm B、2cm C、12cm D、14cm5. 如图,点E、F分别是▱ABCD边AD、BC的中点,G、H是对角线BD上的两点,且BG=DH.则下列结论中错误的是( )
A、 B、 C、 D、4. 已知三角形的两边长分别为6 cm和8 cm,则下列长度的四条线段中能作为第三边上的中线是( )A、1cm B、2cm C、12cm D、14cm5. 如图,点E、F分别是▱ABCD边AD、BC的中点,G、H是对角线BD上的两点,且BG=DH.则下列结论中错误的是( ) A、 B、四边形EGFH是平行四边形 C、 D、6. 如图,在一束平行光线中插入一张对边平行的纸板,如果光线与纸板右下方所成的 , 则光线与纸板左上方所成的的度数是( )
A、 B、四边形EGFH是平行四边形 C、 D、6. 如图,在一束平行光线中插入一张对边平行的纸板,如果光线与纸板右下方所成的 , 则光线与纸板左上方所成的的度数是( ) A、 B、 C、 D、7. 如图,在中, , , 、、分别为、、的中点,连接、 , 则四边形的周长是( )
A、 B、 C、 D、7. 如图,在中, , , 、、分别为、、的中点,连接、 , 则四边形的周长是( ) A、5 B、7 C、9 D、118. 如图,在给定的△ABC中,动点D从点B出发沿BC方向向终点C运动,DEAC交AB于点E,DFAB交AC于点F,O是EF的中点,在整个运动过程中,△OBC的面积的大小变化情况是( )
A、5 B、7 C、9 D、118. 如图,在给定的△ABC中,动点D从点B出发沿BC方向向终点C运动,DEAC交AB于点E,DFAB交AC于点F,O是EF的中点,在整个运动过程中,△OBC的面积的大小变化情况是( ) A、不变 B、一直增大 C、先增大后减小 D、先减小后增大9. 如图,点G为的重心,连接并延长分别交于点E,F.连接 , 若.则的长度为( )
A、不变 B、一直增大 C、先增大后减小 D、先减小后增大9. 如图,点G为的重心,连接并延长分别交于点E,F.连接 , 若.则的长度为( ) A、1.6 B、1.8 C、2.2 D、2.410. 如图,在平行四边形中,E为上一点,且 , , , , 则下列结论:①;②平行四边形周长是24;③;④;⑤E为中点.正确的结论有( )
A、1.6 B、1.8 C、2.2 D、2.410. 如图,在平行四边形中,E为上一点,且 , , , , 则下列结论:①;②平行四边形周长是24;③;④;⑤E为中点.正确的结论有( ) A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题(每题3分,共24分)
-
11. 已知:如图,四边形 中, ,要使四边形 为平行四边形,需添加一个条件是:.(只需填一个你认为正确的条件即可)
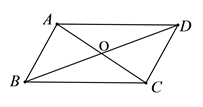 12. 如图,AD为△ABC的中线,延长AD至点E,使DE=AD,连结BE,CE,则判定四边形ABEC是平行四边形的依据是.
12. 如图,AD为△ABC的中线,延长AD至点E,使DE=AD,连结BE,CE,则判定四边形ABEC是平行四边形的依据是. 13. 如图所示,AO=OC,BD=16cm,则当OB=cm时,四边形ABCD是平行四边形。
13. 如图所示,AO=OC,BD=16cm,则当OB=cm时,四边形ABCD是平行四边形。 14. 如图在平行四边形ABCD中,E是CD的中点,F是AE的中点,CF交BE于点G,若BE=8,则GE=.
14. 如图在平行四边形ABCD中,E是CD的中点,F是AE的中点,CF交BE于点G,若BE=8,则GE=. 15. 如图两张长相等,宽分别是1和3的矩形纸片上叠合在一起,重叠部分为四边形ABCD,且AB+BC=6,则四边形ABCD的面积为 .
15. 如图两张长相等,宽分别是1和3的矩形纸片上叠合在一起,重叠部分为四边形ABCD,且AB+BC=6,则四边形ABCD的面积为 . 16. 如图,在ABCD中,点E,F均在AD边上,BE平分∠ABC,CF平分∠BCD,如果BE=8,CF=6,EF=2,那么ABCD的周长等于 .
16. 如图,在ABCD中,点E,F均在AD边上,BE平分∠ABC,CF平分∠BCD,如果BE=8,CF=6,EF=2,那么ABCD的周长等于 . 17. 如图,平行四边形的对角线 , 相交于点O,点E、F分别是线段、的中点,若 , 的周长是18,则 .
17. 如图,平行四边形的对角线 , 相交于点O,点E、F分别是线段、的中点,若 , 的周长是18,则 . 18. 如图,在中,D是上一点, , , 垂足为E,F是的中点, , 则的长为 .
18. 如图,在中,D是上一点, , , 垂足为E,F是的中点, , 则的长为 .
三、解答题(共8题,共66分)
-
19. 如图,在平行四边形ABCD中,点E,F分别在AB,CD上,AE=CF.求证:DE=BF.
 20. 如图所示,在▱中,点 , 是对角线上的两点,且 , 连接 , , , 求证:四边形是平行四边形.
20. 如图所示,在▱中,点 , 是对角线上的两点,且 , 连接 , , , 求证:四边形是平行四边形. 21. 如图,在中, , 、分别是、的中点,试判断四边形的形状,并证明之.
21. 如图,在中, , 、分别是、的中点,试判断四边形的形状,并证明之. 22. 如图,点D、E分别是△ABC的边AB、AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若DE=1,求DF的长.
22. 如图,点D、E分别是△ABC的边AB、AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若DE=1,求DF的长. 23. 如图,点M、N在▱ABCD的对角线AC上,且AM=CN,求证:四边形BMDN是平行四边形.
23. 如图,点M、N在▱ABCD的对角线AC上,且AM=CN,求证:四边形BMDN是平行四边形.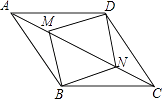 24. 在▱中, , 分别为对角线上两点,连接、、、 , 且 .
24. 在▱中, , 分别为对角线上两点,连接、、、 , 且 . (1)、如图1,求证:四边形是平行四边形;(2)、如图2,若 , 在不添加任何字母及辅助线的情况下,请直接写出图2中面积是面积的的四个三角形.25. 已知,如图,在ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
(1)、如图1,求证:四边形是平行四边形;(2)、如图2,若 , 在不添加任何字母及辅助线的情况下,请直接写出图2中面积是面积的的四个三角形.25. 已知,如图,在ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN. (1)、求证:△AEM≌△CFN;(2)、求证:四边形BMDN是平行四边形.26. 【教材呈现】如图是华师九年级上删数学教材第77页的部分内容.
(1)、求证:△AEM≌△CFN;(2)、求证:四边形BMDN是平行四边形.26. 【教材呈现】如图是华师九年级上删数学教材第77页的部分内容.如图,在中,点D、E分别是与的中点,根据画出的图形,可以猜想:
, 且
对此,我们可以用演绎推理给出证明.

【定理证明】
 (1)、请根据材料内容,结合图①,写出证明过程.(2)、【定理应用】
(1)、请根据材料内容,结合图①,写出证明过程.(2)、【定理应用】
如图②,四边形中,M、N、P分别为、、的中点,边、延长线交于点E, , 则的度数是.(3)、如图③,矩形中, , , 点E在边上,且.将线段绕点A旋转一周,得到线段 , M是线段的中点,直接写出旋转过程中线段长的最大值和最小值.