浙江省温州市2022-2023学年高二上学期数学期末试卷（B卷）

试卷更新日期：2023-02-21 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 $(3 ， - \sqrt{3})$ 是直线的一个方向向量，则该直线的倾斜角为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{2 π}{3}$ D、 $\frac{5 π}{6}$

查看试题解析
2. 已知空间的三个不共面的单位向量 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ ，对于空间的任意一个向量 $\vec{p}$ ，（）

A、将向量 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ 平移到同一起点，则它们的终点在同一个单位圆上 B、总存在实数x，y，使得 $\vec{p} = x \vec{a} + y \vec{b}$ C、总存在实数x，y，z，使得 $\vec{p} = x \vec{a} + y (\vec{a} + \vec{b}) + z (\vec{a} - \vec{b})$ D、总存在实数x，y，z，使得 $\vec{p} = x \vec{a} + y (\vec{a} + \vec{b}) + z (\vec{a} - \vec{c})$

查看试题解析
3. 过两点 $A (3 ， - 5)$ ， $B (- 5 ， 5)$ 的直线在 $y$ 轴上的截距为（）

A、 $- \frac{5}{4}$ B、 $\frac{5}{4}$ C、 $- \frac{2}{5}$ D、 $\frac{2}{5}$

查看试题解析
4. 已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的焦点为 $F_{1} (- c ， 0)$ ， $F_{2} (c ， 0)$ ，且c是a，b的等比中项，则在椭圆上使 $∠ F_{1} P F_{2} = 90 °$ 的点P共有（）

A、0个 B、2个 C、4个 D、8个

查看试题解析
5. 已知 ${a_{n}}$ 是公差不为0的等差数列， $S_{n}$ 是其前 $n$ 项和，则“对于任意 $n \in N^{*}$ ，都有 $S_{n} \leq S_{5}$ ”是“ $a_{6} < a_{5}$ 的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件

查看试题解析
6. 抛物线的光学性质：从焦点出发的光线，经过抛物线上的一点（不同于顶点）反射后，反射光线平行于抛物线的轴．现有抛物线 $C$ ： $y^{2} = 2 p x (p > 0)$ ，一平行于 $x$ 轴的光线射向抛物线，经抛物线两次反射之后，又沿着 $x$ 轴方向射出，若两平行线间的距离的最小值为8，则抛物线的方程为（）

A、 $y^{2} = 2 x$ B、 $y^{2} = 4 x$ C、 $y^{2} = 8 x$ D、 $y^{2} = 16 x$

查看试题解析
7. 已知椭圆 $L_{1}$ ： $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ ，椭圆 $L_{2}$ 与椭圆 $L_{1}$ 的离心率相等，并且椭圆 $L_{1}$ 的短轴端点就是椭圆 $L_{2}$ 的长轴端点，据此类推：对任意的 $n \in N^{*}$ 且 $n \geq 2$ ，椭圆 $L_{n}$ 与椭圆 $L_{n - 1}$ 的离心率相等，并且椭圆 $L_{n - 1}$ 的短轴端点就是椭圆 $L_{n}$ 的长轴端点，由此得到一个椭圆列： $L_{1}$ ， $L_{2}$ ， $⋅ ⋅ ⋅$ ， $L_{n}$ ，则椭圆 $L_{5}$ 的焦距等于（）

A、 $6 \times {(\frac{3}{5})}^{4}$ B、 $6 \times {(\frac{4}{5})}^{4}$ C、 $6 \times {(\frac{3}{5})}^{2}$ D、 $6 \times {(\frac{4}{5})}^{2}$

查看试题解析
8. 正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A B = 2$ ， $A A_{1} = \sqrt{3}$ ， O为BC的中点，M是棱 $B_{1} C_{1}$ 上一动点，过O作 $O N ⊥ A M$ 于点N，则线段MN长度的最小值为（）

A、 $\frac{3 \sqrt{6}}{4}$ B、 $\frac{\sqrt{6}}{2}$ C、 $\frac{3 \sqrt{3}}{4}$ D、 $\sqrt{3}$

查看试题解析

二、多选题

9. 设直线 $l_{1}$ ： $A_{1} x + B_{1} y + C_{1} = 0$ ， $l_{2}$ ： $A_{2} x + B_{2} y + C_{2} = 0$ ，下列说法正确的是（）

A、当 $C_{1} \neq C_{2}$ 时，直线 $l_{1}$ 与 $l_{2}$ 不重合 B、当 $A_{1} B_{2} - A_{2} B_{1} \neq 0$ 时，直线 $l_{1}$ 与 $l_{2}$ 相交 C、当 $A_{1} B_{2} - A_{2} B_{1} = 0$ 时， $l_{1} / / l_{2}$ D、当 $A_{1} A_{2} + B_{1} B_{2} = 0$ 时， $l_{1} ⊥ l_{2}$

查看试题解析
10. 已知空间向量 $\vec{a} = (2 ， - 1 ， 3)$ ， $\vec{b} = (- 4 ， 2 ， x)$ ，下列说法正确的是（）

A、若 $\vec{a} ⊥ \vec{b}$ ，则 $x = \frac{10}{3}$ B、若 $3 \vec{a} + \vec{b} = (2 ， - 1 ， 10)$ ，则 $x = 1$ C、若 $\vec{a}$ 在 $\vec{b}$ 上的投影向量为 $\frac{1}{3} \vec{b}$ ，则 $x = 4$ D、若 $\vec{a}$ 与 $\vec{b}$ 夹角为锐角，则 $x \in (\frac{10}{3} ， + \infty)$

查看试题解析
11. 已知 $S_{n}$ 为数列 ${a_{n}}$ 的前 $n$ 项和，下列说法正确的是（）

A、若 ${a_{n}}$ 为等差数列，则 $S_{5}$ ， $S_{10} - S_{5}$ ， $S_{15} - S_{10}$ 为等差数列 B、若 ${a_{n}}$ 为等比数列，则 $S_{5}$ ， $S_{10} - S_{5}$ ， $S_{15} - S_{10}$ 为等比数列 C、若 ${a_{n}}$ 为等差数列，则 $\frac{S_{5}}{5}$ ， $\frac{S_{10}}{10}$ ， $\frac{S_{15}}{15}$ 为等差数列 D、若 ${a_{n}}$ 为等比数列，则 $\frac{S_{5}}{5}$ ， $\frac{S_{10}}{10}$ ， $\frac{S_{20}}{20}$ 为等比数列

查看试题解析
12. 如图，已知点P是椭圆 $\frac{x^{2}}{16} + \frac{y^{2}}{12} = 1$ 上第一象限内的动点， $F_{1}$ ， $F_{2}$ 分别为椭圆的左、右焦点，圆心在y轴上的动圆T始终与射线 $P F_{1}$ ， $P F_{2}$ 相切，切点分别为M，N，则下列判断正确的是（）

A、 $| P M | = | P N | = 4$ B、 ${| P M |}^{2} \leq | P F_{1} | \cdot | P F_{2} |$ C、 $△ P M N$ 面积的最大值为 $4 \sqrt{3}$ D、当点P坐标为 $(2 \sqrt{3} ， \sqrt{3})$ 时，则直线PT的斜率是 $\frac{2}{3}$

查看试题解析

三、填空题

13. 已知圆 ${(x - 1)}^{2} + y^{2} = 1$ 与圆 $x^{2} + y^{2} + a x + b y = 0$ 内切，则有序实数对 $(a ， b)$ 可以是．（写出一对即可）

查看试题解析
14. 11世纪，阿拉伯数学家阿尔•卡克希利用几何方法推出了自然数的三次方的求和公式（如图所示），据此可知： $1^{3} + 2^{3} + 3^{3} + \cdot \cdot \cdot + 9^{3} =$ ．

查看试题解析
15. 二面角 $α - l - β$ 的棱上有两个点 $A$ 、 $B$ ，线段 $B D$ 与 $A C$ 分别在这个二面角的两个面内，并且垂直于棱 $l$ ，若 $A B = 4$ ， $A C = 6$ ， $B D = 8$ ， $C D = 2 \sqrt{17}$ ，则平面 $α$ 与平面 $β$ 的夹角为.

查看试题解析
16. 已知点 $A (2 ， 2)$ 在抛物线 $y^{2} = 2 p x$ 上，B，C是抛物线上的动点且 $C A ⊥ C B$ ，若直线AC的斜率 $k \in [\frac{1}{2} ， 2]$ ，则点B纵坐标的取值范围是．

查看试题解析

四、解答题

17. 已知点 $P (- 3 ， 2)$ 及圆C： $x^{2} + y^{2} + 2 x + 4 y + 1 = 0$ ．

(1)、求过P且与圆C相切的直线方程；

(2)、以PC为直径的圆交圆C于A，B两点，求 $| A B |$ ．

查看试题解析
18. 长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A D = A A_{1} = 1$ ， $A B = 2$ ，点 $E$ 在棱 $A B$ 上移动．

(1)、求证： $D_{1} E ⊥ A_{1} D$ ；

(2)、当 $E$ 为棱 $A B$ 的中点时，求 $D_{1} E$ 与面 $A C D_{1}$ 所成角的正弦值．

查看试题解析
19. 已知数列 ${a_{n}}$ 满足： $a_{1} = 2$ ， $n a_{n + 1} - (n + 1) a_{n} = - 1$ （ $n \in N^{*}$ ）

(1)、写出 $a_{2}$ ， $a_{3}$ ，并求 ${a_{n}}$ 的通项公式；

(2)、若数列 $b_{n} = \frac{a_{n}}{2^{a_{n}}}$ （ $n \in N^{*}$ ），求数列 ${b_{n}}$ 的前n项和 $S_{n}$ ．

查看试题解析
20. 如图，在四棱锥 $P - A B C D$ 中，底面ABCD为正方形，二面角 $P - B C - A$ 为直二面角． $B P = C P = \sqrt{2}$ ， $B P ⊥ C P$ ， M，N分别为AP，AC的中点．

(1)、求平面BMN与平面PCD夹角的余弦值；

(2)、若平面 $B M N ∩$ 平面 $P C D = l$ ，求点A到直线l的距离．

查看试题解析
21. 已知椭圆 $C_{1}$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 过点 $M (\frac{2 \sqrt{3}}{3} ， \sqrt{2})$ 且与抛物线 $C_{2}$ ： $y^{2} = 2 p x$ 有一个公共的焦点 $F (1 ， 0)$ ．

(1)、求椭圆 $C_{1}$ 与抛物线 $C_{2}$ 的方程；

(2)、过点 $F$ 的直线 $l$ 与椭圆 $C_{1}$ 交于 $A$ ， $B$ 两点，与抛物线 $C_{2}$ 交于 $C$ ， $D$ 两点．是否存在这样的直线 $l$ ，使得 $2 | A B | = | C D |$ ？若存在，求出直线 $l$ 的方程，若不存在，请说明理由．

查看试题解析
22. 广州塔外形优美，游客都亲切地称之为“小蛮腰”，其主塔部分可近似地看成是由一个双曲面和上下两个圆面围成的．其中双曲面的构成原理如图所示：圆 $O_{1}$ ， $O_{2}$ 所在的平面平行， $O_{1} O_{2}$ 垂直于圆面，AB为一条长度为定值的线段，其端点A，B分别在圆 $O_{1}$ ， $O_{2}$ 上，当A，B在圆上运动时，线段AB形成的轨迹曲面就是双曲面．用过 $O_{1} O_{2}$ 的任意一个平面去截双曲面得到的截面曲线都是双曲线，我们称之为截面双曲线．已知主塔的高度 $| O_{1} O_{2} | = 15 (12 + 9 \sqrt{3}) m$ ， $| A B | = 15 (16 + 7 \sqrt{3}) m$ ，设塔身最细处的圆的半径为 $r_{0}$ ，上、下圆面的半径分别为 $r_{1}$ 、 $r_{2}$ ，且 $r_{0}$ ， $r_{1}$ ， $r_{2}$ 成公比为 $\sqrt{2}$ 的等比数列．

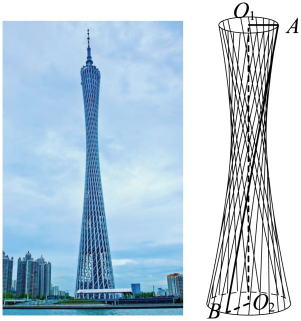(1)、求 $\vec{O_{1} A}$ 与 $\vec{O_{2} B}$ 的夹角；

(2)、建立适当的坐标系，求该双曲面的截面双曲线的渐近线方程．

查看试题解析