上海市2023届高三下学期数学开学摸底试卷

试卷更新日期：2023-02-21 类型：开学考试

进入出卷网下载

一、填空题

1. 已知集合 $A = {y | y = 1 0^{x} ， x \in R}$ ， $B = {y | y = x^{2} ， 1 \leq x \leq 2}$ ，则 $A ∩ B =$ .

查看试题解析
2. 已知函数 $f (x) = 2 + l o g_{a} (x + 1)$ （ $a > 0$ ，且 $a \neq 1$ ）．若 $y = f (x)$ 的反函数的图象经过点 $(1 ， 2)$ ，则 $a =$ ．

查看试题解析
3. 若方程x²﹣2x+3＝0的两个根为α和β，则|α|+|β|＝．

查看试题解析
4. 某学校组织学生参加劳动实践活动，其中4名男生和2名女生参加农场体验活动，体验活动结束后，农场主与6名同学站成一排合影留念，则2名女生互不相邻，且农场主站在中间的概率等于．（用数字作答）

查看试题解析
5. 已知复数 $z$ 满足 $z (2 + i) = 5 (i$ 为虚数单位 $)$ ，则 $z$ 的模为.

查看试题解析
6. 等比数列 ${a_{n}} (n \in N *)$ 中，若 $a_{2} = \frac{1}{16}$ ， $a_{5} = \frac{1}{2}$ ，则 $a_{8} =$ ．

查看试题解析
7. 在 $(x + 2)^{6}$ 的二项展开式中， $x^{3}$ 项的系数为(结果用数值表示).

查看试题解析
8. 若 $s i n θ = k c o s θ$ ，则 $s i n θ \cdot c o s θ$ 的值等于(用 $k$ 表示).

查看试题解析
9. 函数 $y = 3^{x} + \frac{a}{3^{x} + 1}$ 在 $(0, + \infty)$ 内单调递增，则实数 $a$ 的取值范围是.

查看试题解析
10. 设集合 $S ， T ， S \subseteq N^{\cdot} ， T \subseteq N^{\cdot} ， S ， T$ 中，至少有两个元素，且 $S ， T$ 满足：①对于任意 $x ， y \in S$ ，若 $x \neq y$ ，都有 $x y \in T$ ；②对于任意 $x ， y \in T$ ，若 $x < y$ ，则 $\frac{y}{x} \in S$ .若 $S$ 有4个元素，则 $S ∪ T$ 有个元素.

查看试题解析
11. 设 $S_{n}$ 为正数列 ${a_{n}}$ 的前 $n$ 项和， $S_{n + 1} = q S_{n} + S_{1}$ ， $q > 1$ ，对任意的 $n \geq 1$ ， $n \in N$ 均有 $S_{n + 1} \leq 4 a_{n}$ ，则 $q$ 的取值为.

查看试题解析
12. 已知定义在 $(- 3 ， 3)$ 上的奇函数 $y = f (x)$ 的导函数是 $f^{^{'}} (x)$ ，当 $x \geq 0$ 时， $y = f (x)$ 的图象如图所示，则关于x的不等式 $\frac{f^{'} (x)}{x} > 0$ 的解集为.

查看试题解析

二、单选题

13. 已知平面α ，直线m ， n满足m $⊄$ α ， n $\subset$ α ，则“m∥n”是“m∥α”的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
14. 某高科技公司所有雇员的工资情况如下表所示．
年薪（万元）
135
95
80
70
60
52
40
31
人数
1
1
2
1
3
4
1
12
该公司雇员年薪的标准差约为（）

A、24.5（万元） B、25.5（万元） C、26.5（万元） D、27.5（万元）

查看试题解析
15. 已知点 $P (4 ， m)$ 是直线 $l ： {\begin{array}{l} x = 1 + 3 t ， \\ y = - 5 + t \end{array}$ （ $t \in R ， t$ 是参数）和圆 $C ： {\begin{array}{l} x = 1 + 5 c o s θ ， \\ y = 5 s i n θ \end{array}$ （ $θ \in R ， θ$ 是参数）的公共点，过点 $P$ 作圆 $C$ 的切线 $l_{1}$ ，则切线 $l_{1}$ 的方程是（）

A、 $3 x - 4 y - 28 = 0$ B、 $3 x + 4 y - 28 = 0$ C、 $3 x - y - 13 = 0$ D、 $x - 3 y - 16 = 0$

查看试题解析
16. 已知数列 ${x_{n}}$ 满足 $x_{1} = 2$ ， $x_{n + 1} = \sqrt{2 x_{n} - 1} (n \in N^{*})$ .给出以下两个命题：命题 $p :$ 对任意 $n \in N^{*}$ ，都有 $1 < x_{n + 1} < x_{n}$ ；命题 $q :$ 存在 $r \in (0, 1)$ ，使得对任意 $n \in N^{*}$ ，都有 $x_{n} \leq r^{n - 1} + 1$ .则（）

A、p真，q真 B、p真，q假 C、p假，q真 D、p假，q假

查看试题解析

三、解答题

17. 如图，在四棱锥P-ABCD中，已知PA⊥平面ABCD，且四边形ABCD为直角梯形，∠ABC＝∠BAD＝90°，AB＝AD＝AP＝2，BC＝1，且Q为线段BP的中点．

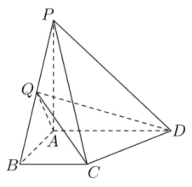(1)、求直线CQ与PD所成角的大小；

(2)、求直线CQ到平面ADQ所成角的大小．

查看试题解析
18. 2020年11月5日至10日，第三届中国国际进口博览会在上海举行，经过三年发展，进博会让展品变商品，让展商变投资商，交流创意和理念，联通中国和世界，国际采购、投资促进、人文交流，开放合作四大平台作用不断凸显，成为全球共享的国际公共产品.在消费品展区，某企业带来了一款新型节能环保产品参展，并决定大量投放市场.已知该产品年固定研发成本为150万元，每生产1万台需另投入380万元.设该企业一年内生产该产品 $x$ 万台且全部售完，每万台的销售收入为 $R (x)$ 万元，且 $R (x) = {\begin{array}{l} 500 - 2 x ， 0 < x \leq 20 \\ 370 + \frac{2140}{x} - \frac{6250}{x^{2}} ， x > 20 \end{array}$ .

(1)、写出年利润 $S$ （万元）关于年产量 $x$ （万台）的函数解析式；（利润 = 销售收入—成本）

(2)、当年产量为多少万台时，该企业获得的年利润最大？并求出最大年利润.

查看试题解析
19. 在平面直角坐标系 $x O y$ 中，已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ （ $a$ 、 $b$ 为正数）的右顶点为 $A$ ，右焦点 $F_{2} (5 ， 0)$ 到渐近线的距离为4，直线 $l$ 与双曲线 $C$ 交于 $P$ 、 $Q$ 两点，且 $P$ 、 $Q$ 均不是双曲线的顶点， $M$ 为 $P Q$ 的中点．

(1)、求双曲线的方程；

(2)、当直线 $P Q$ 与直线 $O M$ 的斜率均存在时，设斜率分别为 $k_{1}$ 、 $k_{2}$ ，求 $k_{1} k_{2}$ 的值；

(3)、若 $\frac{| A M |}{| P Q |} = \frac{1}{2}$ ，试探究直线 $l$ 是否过定点？若过定点，求出该定点坐标：否则，说明理由．

查看试题解析
20. 已知在每一项均不为0的数列 ${a_{n}}$ 中， $a_{1} = 3$ ，且 $a_{n + 1} = p a_{n} + \frac{t}{a_{n}}$ （ $p$ 、 $t$ 为常数， $n \in N^{*}$ ），记数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ .

(1)、当 $t = 0$ 时，求 $S_{n}$ ；

(2)、当 $p = \frac{1}{2}$ 、 $t = 2$ 时，
①求证：数列 ${l g \frac{a_{n} + 2}{a_{n} - 2}}$ 为等比数列；
②是否存在正整数 $m$ ，使得不等式 $S_{n} - 2 n < m$ 对任意 $n \in N^{*}$ 恒成立？若存在，求出 $m$ 的最小值；若不存在，请说明理由.

查看试题解析
21. 设函数 $f (x) = a x^{3} - (a + 1) x^{2} + x ， g (x) = k x + m$ ，其中 $a \geq 0 ， k ， m \in R$ ，若任意 $x \in [0 ， 1]$ 均有 $f (x) \leq g (x)$ ，则称函数 $y = g (x)$ 是函数 $y = f (x)$ 的控制函数”，且对于所有满足条件的函数 $y = g (x)$ 在 $x$ 处取得的最小值记为 $\bar{f} (x)$ ．

(1)、若 $a = 2 ， g (x) = x$ ，试问 $y = g (x)$ 是否为 $y = f (x)$ 的控制函数”；

(2)、若 $a = 0$ ，使得直线 $y = h (x)$ 是曲线 $y = f (x)$ 在 $x = \frac{1}{4}$ 处的切线，证明：函数 $y = h (x)$ 为函数 $y = f (x)$ 的控制函数，并求“ $\bar{f} (\frac{1}{4})$ ”的值；

(3)、若曲线 $y = f (x)$ 在 $x = x_{0} (x_{0} \in (0 ， 1))$ 处的切线过点 $(1 ， 0)$ ，且 $c \in [x_{0} ， 1]$ ，证明：当且仅当 $c = x_{0}$ 或 $c = 1$ 时， $\bar{f} (c) = f (c)$ ．

查看试题解析

年薪（万元）	135	95	80	70	60	52	40	31
人数	1	1	2	1	3	4	1	12