山西省太原市2023届高三上学期数学期末试卷
试卷更新日期:2023-02-21 类型:期末考试
一、单选题
-
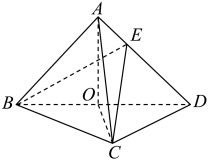
1. 已知集合 , 则( )A、 B、 C、 D、2. 设复数满足为虚数单位),则复数在复平面内所对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 已知 , 则向量与的夹角为( )A、 B、 C、 D、4. 中国古代数学的瑰宝《九章算术》中记载了一种称为“曲池”的几何体,该几何体是上、下底面均为扇环形的柱体(扇环是指圆环被扇形截得的部分).现有一个如图所示的曲池,垂直于底面, , , 底面扇环所对的圆心角为 , 弧的长度是弧长度的2倍, , 则该曲池的体积为( )
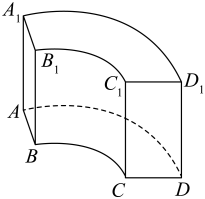 A、 B、 C、 D、5. 某学校音乐社团为庆祝学校百年华诞将举办歌曲展演,要从4首独唱歌曲和2首合唱歌曲中选出4首歌曲安排演出,若最后一首歌曲必须是合唱歌曲,则不同的安排方法种数为( )A、96 B、120 C、240 D、3606. 已知 , 则( )A、 B、 C、 D、7. 如表所示的数阵称为“森德拉姆素数筛”,表中每行每列的数都成等差数列,设表示该数阵中第m行、第n列的数,则下列说法正确的是( )
A、 B、 C、 D、5. 某学校音乐社团为庆祝学校百年华诞将举办歌曲展演,要从4首独唱歌曲和2首合唱歌曲中选出4首歌曲安排演出,若最后一首歌曲必须是合唱歌曲,则不同的安排方法种数为( )A、96 B、120 C、240 D、3606. 已知 , 则( )A、 B、 C、 D、7. 如表所示的数阵称为“森德拉姆素数筛”,表中每行每列的数都成等差数列,设表示该数阵中第m行、第n列的数,则下列说法正确的是( )2
3
4
5
6
7
…
3
5
7
9
11
12
…
4
7
10
13
16
19
…
5
9
13
17
21
25
…
6
11
1
21
26
31
…
7
13
19
25
31
37
…
…
…
…
…
…
…
…
A、 B、 C、 D、8. 已知函数及其导函数的定义域均为 , 记 , 若均为偶函数,当时, , 且 , 则( )A、20 B、30 C、35 D、40二、多选题
-
9. 已知正数x,y满足 , 则下列结论正确的是( )A、的最大值是1 B、的最小值是4 C、的最大值是 D、的最小值是110. 已知函数的部分图像如图所示,下列结论正确的是( )
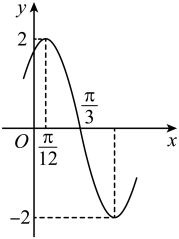 A、的图像关于直线对称 B、的图像关于点对称 C、将函数的图像向左平移个单位长度可以得到函数的图像 D、方程在上有7个不相等的实数根11. 已知抛物线的焦点为 , 过点的直线交于两个不同点,则下列结论正确的是( )A、若点 , 则的最小值是3 B、的最小值是2 C、若 , 则直线的斜率为 D、过点分别作抛物线的切线,设两切线的交点为 , 则点的横坐标为-112. 已知正四棱柱的底面边长为2,侧棱 , P为上底面上的动点,M为棱的中点,下列结论正确的是( )A、三棱锥的体积为定值1 B、当直线与平面所成角为时,点P的轨迹长度为 C、若直线平面 , 则线段长度的最小值为 D、直线被正四棱柱外接球所截得线段长度的取值范围是
A、的图像关于直线对称 B、的图像关于点对称 C、将函数的图像向左平移个单位长度可以得到函数的图像 D、方程在上有7个不相等的实数根11. 已知抛物线的焦点为 , 过点的直线交于两个不同点,则下列结论正确的是( )A、若点 , 则的最小值是3 B、的最小值是2 C、若 , 则直线的斜率为 D、过点分别作抛物线的切线,设两切线的交点为 , 则点的横坐标为-112. 已知正四棱柱的底面边长为2,侧棱 , P为上底面上的动点,M为棱的中点,下列结论正确的是( )A、三棱锥的体积为定值1 B、当直线与平面所成角为时,点P的轨迹长度为 C、若直线平面 , 则线段长度的最小值为 D、直线被正四棱柱外接球所截得线段长度的取值范围是三、填空题
-
13. 已知函数的图象在处的切线经过坐标原点,则实数 .14. 的展开式中常数项为 . (用数字作答)15. 在临床上,经常用某种试验来诊断试验者是否患有某种癌症,设“试验结果为阳性”,“试验者患有此癌症”,据临床统计显示 , . 已知某地人群中患有此种癌症的概率为0.001,现从该人群中随机抽在了1人,其试验结果是阳性,则此人患有此种癌症的概率为 .16. 已知双曲线的左、右焦点分别为 , 过作圆的切线,切点为 , 延长交双曲线的左支于点 . 若 , 则双曲线离心率的取值范围是 .
四、解答题
-
17. 已知数列的前n项和为 .(1)、从条件①、条件②这两个条件中选择一个条件作为已知,求的通项公式;(2)、设 , 记的前n项和为 , 若对任意正整数的n,不等式恒成立,求的最小值.
条件① , 且;条件②为等比数列,且满足;(注:若条件①和条件②分别解答,按第一个解答计分.)
18. 在中,内角 , , 所对的边分别为 , , , 且满足 .(1)、求证:;(2)、求的取值范围.19. 从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,整理测量结果得到如下频率分布直方图: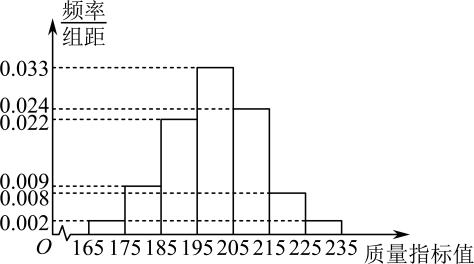 (1)、求这500件产品质量指标值的样本平均值和样本方差(同一组的数据用该组区间的中点值作代表);(2)、由直方图可以认为,这种产品的质量指标Z服从正态分布 , 其中近似为样本平均数近似为样本方差 .
(1)、求这500件产品质量指标值的样本平均值和样本方差(同一组的数据用该组区间的中点值作代表);(2)、由直方图可以认为,这种产品的质量指标Z服从正态分布 , 其中近似为样本平均数近似为样本方差 .(ⅰ)利用该正态分布,求;
(ⅱ)某用户从该企业购买了100件这种产品,记X表示这100件产品中质量指标值位于区间的产品件数.利用(ⅰ)的结果,求 .
附:;若 , 则 .