浙江省杭州市十三中教育集团2022-2023学年九年级上学期数学期末独立作业

试卷更新日期：2023-02-21 类型：期末考试

进入出卷网下载

一、选择题（本题共有10个小题，每小题3分，共30分）

1. 若 $\frac{a}{b} = \frac{4}{7}$ ，则 $\frac{a}{b + a}$ 的值为（）

A、 $\frac{4}{11}$ B、 $\frac{3}{4}$ C、 $\frac{3}{11}$ D、 $\frac{3}{7}$

查看试题解析
2. 抛一枚均匀的骰子，下列事件中，发生可能性最大的是（）

A、点数是奇数 B、点数是3的倍数 C、点数大于5 D、点数小于5

查看试题解析
3. 两个相似三角形的相似比是4：9，则它们的面积比是（）

A、4：9 B、16：81 C、2：3 D、1：3

查看试题解析
4. 如图，已知圆心角∠AOB=140°，则圆周角∠ACB=（）

A、40° B、70° C、110° D、120°

查看试题解析
5. 关于二次函数 $y = - {(x + 2)}^{2} - 3$ 的图象，下列说法错误的是（）

A、开口向下 B、对称轴是直线x=2 C、与x轴没有交点 D、当x＞ $- 1$ 时，y随x的增大而减小

查看试题解析
6. 如图，AB是⊙O的直径，弦CD⊥AB交于点E. 若BE=10，CD=8，则⊙O的半径为（）

A、3 B、4.2 C、5.8 D、6

查看试题解析
7. 已知在△ABC中，AB=6，AC=9，D，E分别是AB，AC边上的点，且AD=2. 若△ABC和△ADE相似，则AE=（）

A、5 B、3 C、 $\frac{4}{3}$ D、3或 $\frac{4}{3}$

查看试题解析
8. 已知抛物线 $y = x^{2} + (m + 3) x + m$ . 当x=1时，y＞0；当x＜ $- 2$ 时，y随x的增大而减小，则m的取值范围是（）

A、 $m > - 2$ B、 $m \geq 1$ C、 $- 2 < m \leq 1$ D、 $- 2 < m \leq 2$

查看试题解析
9. 如图，等边△ABC是⊙O的内接三角形，点D，E分别为AB，AC边上的中点，延长DE交⊙O于点F，若BC=2，则EF=（）

A、 $\frac{\sqrt{5} - 1}{2}$ B、 $\sqrt{3} - 1$ C、 $\frac{2 \sqrt{3}}{3} - \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
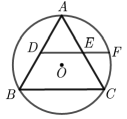10. 如图，将矩形ABCD沿着GE，EC，GF翻折，使得点A，B，D恰好都落在点O处，且点G，O，C在同一条直线上，点E，O，F 在另一条直线上. 以下结论正确的是（）

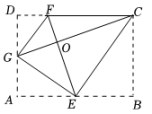A、△COF∽△CEG B、OC=3OF C、AB：AD=4：3 D、GE= $\sqrt{6}$ DF

查看试题解析

二、填空题（本题共有6个小题，每小题4分，共24分）

11. 一个边长为2的正六边形，其外接圆的半径为.

查看试题解析
12. 在一个不透明的袋子里装有红球、黄球共20个，这些球除颜色外都相同. 小明通过多次实验发现，摸出红球的频率稳定在0.3左右，则袋子中红球的大约有个.

查看试题解析
13. 已知扇形的圆心角为80°，半径为3，则该扇形的面积为，周长为.（结果保留π）

查看试题解析
14. 如图，将△ABC以点A为旋转中心逆时针旋转得到△ADE，当点D在BC边上时，恰好有AE∥BC，若∠C=40°，则∠B=.

查看试题解析
15. 如图，在△ABC中，点D，E分别在BC，AC上，CD=2BD，CE=2AE，BE交AD于点F，则AF：FD= ， S_△_BFD：S_△_ABC=.

查看试题解析
16. 已知关于x的一元二次方程 $(x - 2) (x - 3) = m$ 有实根x₁ ， x₂ ，且x₁＜x₂ ，现有下列说法： ①当m=0时，x₁=2，x₂=3；②当m>0时，2＜x₁＜x₂＜3；③ $m > - \frac{1}{4}$ ；④二次函数 $y = (x - x_{1}) (x - x_{2}) - m$ 的图象与x轴的交点坐标为（2，0）和（3，0）. 其中正确的有.

查看试题解析

三、解答题（本题共有7个小题，共66分）

17. 如图，△ABC的顶点均为网格中的格点.

(1)、选择合适的格点（包括边界）为点D和点E，请画出一个△ADE，使△ADE∽△ABC（相似比不为1）.

(2)、证明：△ADE∽△ABC.

查看试题解析
18. 已知二次函数 $y = x^{2} + b x + c$ 经过（0， $- 2$ ）和（1， $- 2$ ）．

(1)、求该二次函数的表达式和对称轴.

(2)、当 $- 1 \leq x \leq 3$ 时，求该二次函数的最大值和最小值.

查看试题解析
19. 2022年世界杯在卡塔尔举办. 赛前通过抽签，将32支参赛队伍分为8组（A组、B组、C组、D组、E组、F组、G组和H组），每4支队伍一组. 每组的4支队伍通过组内循环赛决出第一名和第二名晋级十六强.

(1)、在抽签时，求甲队进入E组的概率（甲队进入各组的可能性相同）.

(2)、已知甲、乙、丙、丁四支队伍同在E组，且四支队伍晋级十六强的可能性相同，请用列表或画树状图的方法求甲、乙两支队伍同时晋级十六强的概率.

查看试题解析
20. 如图，在▱ABCD中，M，N为对角线BD的三等分点，直线AM交BC于点E，直线EN交AD于点F.

(1)、找出图中的两对相似三角形，选一对说明理由.

(2)、试探究AD与FD之间的数量关系，并说明理由.

查看试题解析
21. 如图，△ABC内接于⊙O，AB是⊙O的直径，AB=10，AC=6. 连接OC，弦AD分别交OC，BC于点E，F，其中E是AD的中点.

(1)、求证：∠CAD=∠CBA.

(2)、求OE的长.

查看试题解析
22. 已知二次函数 $y = a x^{2} - 2 (a + 1) x + 4 (a \neq 0)$ .

(1)、证明：二次函数的图象与x轴总有交点.

(2)、若点 $P (\frac{1}{a} ， b)$ 和点 $Q (\frac{1}{a} + n ， b)$ 在该二次函数图象上，求 ${(\frac{1}{a} + b)}^{2} + n^{2}$ 的值.

(3)、将该二次函数图象向下平移2个单位，令新函数图象与x轴的交点横坐标为x₁ ， x₂.
证明： $| x_{1} - x_{2} | > 2$ .

查看试题解析
23. 如图，AB、AC、AD是⊙O中的三条弦，点E在AD上，且AB=AC=AE. 连结BC，BD，CD，其中BC交AD于点G.

(1)、求证：△ABG∽△ADB.

(2)、若∠DBE=α，求∠CAD的度数（用含α的代数式表示）.

(3)、若AD=15，AB=12，BD=6，求线段CD的长.

查看试题解析