陕西省榆林市府谷县2022-2023学年九年级上学期期末数学试题

试卷更新日期：2023-02-21 类型：期末考试

进入出卷网下载

一、单选题

1.
如图所示的圆锥的主视图是（）

A、 B、 C、 D、

查看试题解析
2. 正方形具有而菱形不一定有的性质是（）

A、对角线互相垂直 B、对角线相等 C、对角相等 D、邻边相等

查看试题解析
3. 反比例函数 $y = \frac{m - 1}{x}$ 的图象在第二、四象限，则m可能取的一个值为（）.

A、1 B、4 C、0 D、2

查看试题解析
4. 下列各组图形中一定相似的是（）.

A、两个直角三角形 B、两个等边三角形 C、两个菱形 D、两个矩形

查看试题解析
5. 如图，在 $△ A B C$ 中，D，E分别是 $A B ， A C$ 上的点.且 $D E ∥ B C$ .若 $\frac{A D}{B D} = \frac{5}{3}$ ， $C E = 9 c m$ ，则 $A E$ 的长是（）.

A、 $13 c m$ B、 $18 c m$ C、 $16 c m$ D、 $15 c m$

查看试题解析
6. 关于x的一元二次方程 $x^{2} + b x + c = 0$ 的两个实数根分别为1和-1，则 $b^{2} - c^{2}$ 的值为（）.

A、-1 B、1 C、2 D、-2

查看试题解析
7. 如图，在 $△ A B C$ 中，点D、E分别在AC、AB上，连接DE，若 $∠ A E D = ∠ C$ ，且 $B C = 2 D E$ ，则 $\frac{△ A D E 的周长}{△ A B C 的周长}$ 的值为（）.

A、 $\frac{2}{3}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
8. 若 $M (- 6 ， a)$ ， $N (2 ， b)$ ， $P (6 ， c)$ 三点都在反比例函数 $y = \frac{m^{2} + 1}{x}$ 的图象上，则a、b、c的大小关系为（）.

A、 $a > b > c$ B、 $b > c > a$ C、 $c > a > b$ D、 $c > b > a$

查看试题解析

二、填空题

9. 小华在解方程 $x^{2} = 8 x$ 时，只得出一个根是 $x = 8$ ，则被他漏掉的一个根是 $x =$ .

查看试题解析
10. 如图，物体在灯泡发出的光照射下形成的影子是投影.（填“平行”或“中心”）.

查看试题解析
11. 抛掷一枚质地均匀的硬币2次，2次抛掷的结果都是正面朝上的概率是.

查看试题解析
12. 如图，在平面直角坐标系中，点 $B$ 在 $y$ 轴上， $A B = A O$ ，反比例函数 $y = \frac{k}{x} (x < 0)$ 的图象经过点 $A$ ，若 $S_{△ A B O} = 3$ ，则 $k$ 的值为．

查看试题解析
13. 如图，菱形 $A B C D$ 中， $A B = 5$ ，对角线 $A C = 6$ ， E为 $A D$ 上一点且 $A E = 1$ ，连接 $B E$ 交 $A C$ 于点F，过点F作 $F G ⊥ B C$ 于点G，则 $F G$ 的长度为.

查看试题解析

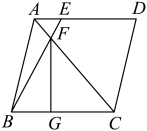
三、解答题

14. 解方程： $x (x - 2) = 15$ .

查看试题解析
15. 有四张背面完全相同，正面涂有红色或绿色的卡片，其中三张卡片的颜色分别是红色、绿色，绿色，第四张卡片的颜色未知.将这四张卡片背面朝上，洗匀，从中随机抽取一张，记录颜色，然后放回，大量重复试验，共抽了600次，发现有300次抽到红色卡片.第四张卡片是什么颜色的？请通过计算说明.

查看试题解析
16. 如图，在 $△ A B C$ 中， $B C = 8 ， A C = 4$ ， D是 $B C$ 边上一点， $C D = 2$ .求证 $△ A B C ∽ D A C$ .

查看试题解析
17. 蓄电池的电压为定值，使用此电源时，电流I（A）是电阻R（Ω）的反比例函数，其图象如图所示．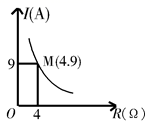

(1)、求这个反比例函数的表达式；

(2)、当R=10Ω时，求电流I（A）．

查看试题解析
18. 如图，在平面直角坐标系中，四边形OABC的顶点坐标分别为 $O (0 ， 0)$ ， $A (4 ， 0)$ ， $B (6 ， 4)$ ， $C (0 ， 6)$ ，将其顶点的坐标缩小为原来的 $\frac{1}{2}$ ，画出得到的四边形 $O A^{'} B^{'} C^{'}$ .并判断这两个四边形是位似图形吗？若是，四边形 $O A^{'} B^{'} C^{'}$ 与四边形 $O A B C$ 的相似比是多少？

查看试题解析
19. 如图，在矩形 $A B C D$ 中，对角线 $A C 、 B D$ 相交于点O.

(1)、若 $∠ O A B = 45 °$ ，求证：矩形 $A B C D$ 是正方形；

(2)、请添加一个异于（1）的条件，使矩形 $A B C D$ 成为正方形，不用说明理由.

查看试题解析
20. 如图是一个组合（由两种常见的几何体组合）几何体的两种视图.

(1)、请写出这个组合几何体是由哪两种几何体组成的；

(2)、画出该组合几何体的左视图.

查看试题解析
21. 已知矩形ABCD两邻边AB、BC的长是关于x的方程 $x^{2} - 2 m x + 4 m - 4 = 0$ 的两个实数根.当m为何值时，矩形ABCD的两邻边AB、BC的长相等.

查看试题解析
22. 假期，小敏和晓梅两家准备从以下四条生态特色旅游线路中各自任意选择一条去游玩，每条线路被选择的可能性相同.
A
B
C
D
观赏红叶
“秦岭四宝”寻踪
“东方红宝石”朱鹮
森林康养

(1)、求小敏家选择线路“观赏红叶”的概率是多少?

(2)、用画树状图或列表的方法，求小敏和晓梅两家恰好选择同一条线路的概率.

查看试题解析
23. 如图，某墙壁左侧有一木杆 $D P$ 和一棵松树 $A B$ .某一时刻在太阳光下，木杆 $D P$ 的影子刚好不落在墙壁上，已知 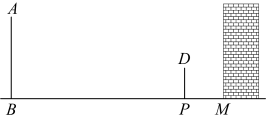$A B ⊥ B P$ ， $D P ⊥ B P$ .

(1)、请画出在同一时刻下松树AB在阳光下的投影 $B C$ ；

(2)、若木杆 $D P = 2 m$ ，木杆DP的投影 $P M = 2.5 m$ ，同一时刻松树AB在阳光下的投影 $B C = 10 m$ ，求松树 $A B$ 的高度.

查看试题解析
24. 列方程（组）解应用题
端午节期间，某水果超市调查某种水果的销售情况，下面是调查员的对话：

小王：该水果的进价是每千克22元；

小李：当销售价为每千克38元时，每天可售出160千克；若每千克降低3元，每天的销售量将增加120千克．

根据他们的对话，解决下面所给问题：超市每天要获得销售利润3640元，又要尽可能让顾客得到实惠，求这种水果的销售价为每千克多少元？

查看试题解析
25. 如图，点O是坐标原点，△OBA∽△DOC ，边OA、OC都在x轴的正半轴上．已知点B的坐标为（12，16），∠BAO＝∠OCD＝90°，OD＝10，反比例函数的图象经过点D ，交AB边于点E ．

(1)、求该反比例函数的解析式；

(2)、求BE的长．

查看试题解析
26. 综合与实践
在数学课上，王老师让同学们对两个全等的直角三角形纸片进行摆弄，如图1， $R t △ A B C ≌ R t △ D E F$ ， $∠ A C B = ∠ D F E = 90 °$ .

(1)、如图2，将图1的两个直角三角形的斜边AB、DE重合，得到“筝形ACBF”，连接CF交AB于点O，若 $A F = 2 B C$ ，则 $S_{△ C B O} ： S_{△ A F O} =$ ；

(2)、如图3，将图1的两个直角三角形直角顶点C与顶点F重合， $A B ∥ D E$ ，连接BE，AD，求证：四边形ADEB是矩形；

(3)、如图4，将图1的两个直角三角形的边AB、DE放到同一直线上，点C、F在AB的同侧，连接CE，AF，CF，若点E是AB的中点.请判断四边形CEAF的形状，并说明理由.

查看试题解析

A	B	C	D
观赏红叶	“秦岭四宝”寻踪	“东方红宝石”朱鹮	森林康养