陕西省西安市2022-2023学年九年级上学期数学期末考试
试卷更新日期:2023-02-21 类型:期末考试
一、单选题
-
1. 下列各点中在反比例函数y=﹣的图象上的是( )A、(﹣2,1) B、(1,﹣2) C、(﹣ , 1) D、( , ﹣2)2. 如图是一个空心圆柱体,其主视图是( )
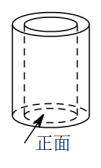 A、
A、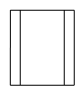 B、
B、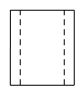 C、
C、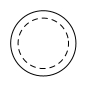 D、
D、 3. 用配方法解一元二次方程时,以下变形正确的是( )A、 B、 C、 D、4. 如图,在平面直角坐标系中,矩形 与矩形 是以点 为位似中心的位似图形,点 的坐标为 ,若 ,则 的长是( )
3. 用配方法解一元二次方程时,以下变形正确的是( )A、 B、 C、 D、4. 如图,在平面直角坐标系中,矩形 与矩形 是以点 为位似中心的位似图形,点 的坐标为 ,若 ,则 的长是( ) A、3 B、4 C、4.5 D、65. 某小组作“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )
A、3 B、4 C、4.5 D、65. 某小组作“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )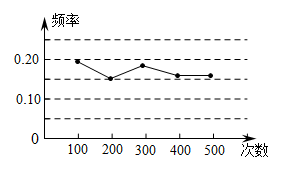 A、掷一个质地均匀的正六面体骰子,向上的面点数是4 B、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 C、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” D、暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球6. 如果两点和都在反比例函数的图象上,那么( )A、 B、 C、 D、7. 如图,是内一点, , , , , 、、、分别是、、、的中点,则四边形的周长是( )
A、掷一个质地均匀的正六面体骰子,向上的面点数是4 B、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 C、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” D、暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球6. 如果两点和都在反比例函数的图象上,那么( )A、 B、 C、 D、7. 如图,是内一点, , , , , 、、、分别是、、、的中点,则四边形的周长是( ) A、14 B、18 C、20 D、228. 如图,F是线段 上除端点外的一点,将 绕正方形 的顶点A顺时针旋转 ,得到 .连接 交 于点H.下列结论正确的是( )
A、14 B、18 C、20 D、228. 如图,F是线段 上除端点外的一点,将 绕正方形 的顶点A顺时针旋转 ,得到 .连接 交 于点H.下列结论正确的是( )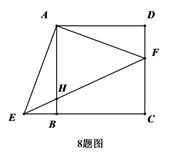 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 若一元二次方程有两个相等的实数根,则的值是.10. 若 , 则的值为.11. 在一个不透明的口袋中装有4个红球和若干白球,它们除颜色外其他完全相同.通过多次摸球试验后发现,摸到红球的频率稳定在左右,则口袋中白球可能有个.12. 如图,一次函数与反比例函数在第一象限交于点 , 与坐标轴分别交于点 , .若是的中点,则的值为.
 13. 如图,矩形中, , 为的中点,为上一动点,为中点,连接 , 则的最小值是.
13. 如图,矩形中, , 为的中点,为上一动点,为中点,连接 , 则的最小值是.
三、解答题
-
14. 解方程:15. 已知的三边长分别为6,8,10,和相似的的最长边长为30,求的周长.16. 如图,在中, , 若 , 求的长.
 17. 如图,等腰的顶角.请用尺规作图法,在上求作一点 , 使得.(保留作图痕迹,不写作法)
17. 如图,等腰的顶角.请用尺规作图法,在上求作一点 , 使得.(保留作图痕迹,不写作法) 18. 如图,点是菱形对角线上的一点, , 求的长.
18. 如图,点是菱形对角线上的一点, , 求的长. 19. 如图,在平面直角坐标系中,已知线段与线段关于原点中心对称,点是点的对应点,点是点的对应点.
19. 如图,在平面直角坐标系中,已知线段与线段关于原点中心对称,点是点的对应点,点是点的对应点.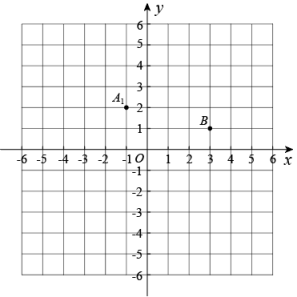
⑴画出线段和;
⑵画出线段以点为位似中心,位似比为的线段.
20. 如图是两个圆形转盘,第一个转盘被平均分成“1”“2”两个区域,第二个转盘被平均分成“1”“2”“3”“4”四个区域. (1)、旋转第一个转盘一次,指针落在“2”区域的概率是;(2)、同时旋转两个转盘,用画树状图或列表的方法求两个转盘的指针都不落在“1”区域的概率.21. 在数学探究活动中,李明同学想利用影子测量旗杆的高度,他在某一时刻测得1m长的标杆影长为 , 同时当他测量教学楼前的旗杆的影长时,因旗杆靠近教学楼,有一部分影子在墙上,他测得旗杆到教学楼的距离 , 旗杆在教学楼墙上的影长 , 求旗杆的高.
(1)、旋转第一个转盘一次,指针落在“2”区域的概率是;(2)、同时旋转两个转盘,用画树状图或列表的方法求两个转盘的指针都不落在“1”区域的概率.21. 在数学探究活动中,李明同学想利用影子测量旗杆的高度,他在某一时刻测得1m长的标杆影长为 , 同时当他测量教学楼前的旗杆的影长时,因旗杆靠近教学楼,有一部分影子在墙上,他测得旗杆到教学楼的距离 , 旗杆在教学楼墙上的影长 , 求旗杆的高.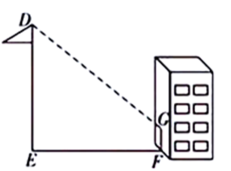 22. “疫情”期间,某商场积压了一批商品,现欲尽快清仓,确定降价促销.据调查发现,若每件商品盈利50元时,可售出500件,商品单价每下降1元,则可多售出20件.设每件商品降价x元.(1)、每件商品降价x元后,可售出商品件(用含x的代数式表示);(2)、若要使销售该商品的总利润达到28000元,求x的值.23. 电灭蚊器的电阻随温度变化的大致图象如图所示,通电后温度由室温上升到时,电阻与温度成反比例函数关系,且在温度达到时,电阻下降到最小值,随后电阻随温度升高而增加,电阻与温度之间的函数式为.
22. “疫情”期间,某商场积压了一批商品,现欲尽快清仓,确定降价促销.据调查发现,若每件商品盈利50元时,可售出500件,商品单价每下降1元,则可多售出20件.设每件商品降价x元.(1)、每件商品降价x元后,可售出商品件(用含x的代数式表示);(2)、若要使销售该商品的总利润达到28000元,求x的值.23. 电灭蚊器的电阻随温度变化的大致图象如图所示,通电后温度由室温上升到时,电阻与温度成反比例函数关系,且在温度达到时,电阻下降到最小值,随后电阻随温度升高而增加,电阻与温度之间的函数式为. (1)、当时,求与之间的关系式;(2)、电灭蚊器在使用过程中,温度在什么范围内时,电阻不超过?24. 如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.
(1)、当时,求与之间的关系式;(2)、电灭蚊器在使用过程中,温度在什么范围内时,电阻不超过?24. 如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB. (1)、求证: ;(2)、若AB⊥AC,AE:EC=1:2,F是BC中点,求证:四边形ABFD是菱形.25. 如图,一次函数的图像与轴和轴分别交于两点,与反比例函数的图像分别交于两点.
(1)、求证: ;(2)、若AB⊥AC,AE:EC=1:2,F是BC中点,求证:四边形ABFD是菱形.25. 如图,一次函数的图像与轴和轴分别交于两点,与反比例函数的图像分别交于两点. (1)、动点在线段上(不与点重合),过点作轴和轴的垂线,垂足为.当矩形的面积为2时,求出点的位置;(2)、在轴上是否存在点 , 使得以为顶点的三角形与相似?若存在,求出点的坐标;若不存在,请说明理由.26. 【问题提出】
(1)、动点在线段上(不与点重合),过点作轴和轴的垂线,垂足为.当矩形的面积为2时,求出点的位置;(2)、在轴上是否存在点 , 使得以为顶点的三角形与相似?若存在,求出点的坐标;若不存在,请说明理由.26. 【问题提出】 (1)、如图①,矩形的四个顶点都在的三条边上,其中 , 求矩形的面积;(2)、【问题解决】
(1)、如图①,矩形的四个顶点都在的三条边上,其中 , 求矩形的面积;(2)、【问题解决】
小红同学参加了物理课外兴趣小组.图②是其制作的一个光电感应装置在某时刻的平面情景图,在边长为的正方形中,为的中点,点位置是一个激光发射器,可以左右来回转动,同时在正方形内发出两条互相垂直的蓝色光线 , 点是落在三边上的两个光点,三点会在正方形内自动感应出一个发光 , 请问在激光器转动发射的过程中,形成的面积有无最大值,如果有,请求出这个最大值;如果没有,请说明理由.