陕西省渭南市蒲城县2022-2023学年八年级上学期期末线上数学质量检测卷
试卷更新日期:2023-02-21 类型:期末考试
一、单选题
-
1. 64的平方根是( )A、 ±8 B、±4 C、±2 D、82. 对假命题“若 , 则”举反例,正确的反例是( )A、 , B、 , C、 , D、 ,3. 已知 , a介于两个连续自然数之间,则下列结论正确的是( )A、 B、 C、 D、4. 把 的图像沿y轴向下平移5个单位后所得图象的关系式是( )A、 B、 C、 D、5. 二元一次方程组的解是( )A、 B、 C、 D、6. 如图, , 下列推理正确的是( )
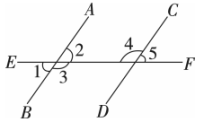
①若 , 则;②若 , 则;③若 , 则;④若 , 则.
A、①② B、②④ C、②③④ D、②③7. “杂交水稻之父”袁隆平培育的超级杂交稻在全世界推广种植.某种植户为了考察所种植的杂交水稻苗的长势,从稻田中随机抽取株水稻苗,测得苗高(单位:)分别是:23,24,23,25,26,23,25.则这组数据的众数和中位数分别是( )A、24,25· B、23,23 C、23,24 D、24,248. 今年9月23日是第五个中国农民丰收节,小彬用打印机制作了一个底面周长为 , 高为的圆柱粮仓模型.如图是底面直径,是高.现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过 , 两点(接头不计),则装饰带的长度最短为( )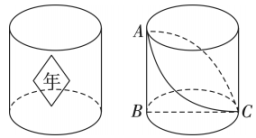 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 点关于y轴的对称点P′的坐标是.10. 请你写出一个比1大且比2小的无理数,该无理数可以是.11. 若点 , 在一次函数的图像上,则 , 的大小关系是.(用“<”连接)12. 如图,在三角形中, , , 则外角的度数为.
 13. 某快递公司每天上午7:00-8:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,下列说法:
13. 某快递公司每天上午7:00-8:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,下列说法: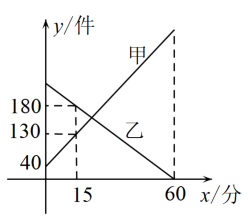
①15分钟后,甲仓库内快件数量为180件;
②乙仓库每分钟派送快件数量为4件;
③8:00时,甲仓库内快件数为600件;
④7:20时,两仓库快递件数相同.
其中正确的个数为 .
三、解答题
-
14. 计算:.15. 解二元一次方程组:16. 已知实数的一个平方根是 , 的立方根是 , 求的算术平方根.17. 已知:与成正比例,且当 时,(1)、求与之间的函数表达式;(2)、当时,的值是多少?18. 如图,在平面直角坐标系中,的三个顶点坐标为 , , , 在图中作出关于轴对称的图形 , 其中点 , , 的对应点分别为点 , , .并写出 , 的坐标.
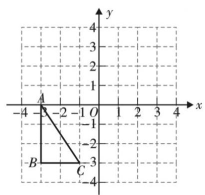 19. 已知点 , 试分别根据下列条件,求点的坐标.(1)、点在轴上;(2)、点到两坐标轴的距离相等.20. 某学校评选先进班集体,从“学习”、“卫生”、纪律”、活动参与”四个方面考核打分,各项满分均为100分,按比例计算综合得分,各项所占比例如表所示:
19. 已知点 , 试分别根据下列条件,求点的坐标.(1)、点在轴上;(2)、点到两坐标轴的距离相等.20. 某学校评选先进班集体,从“学习”、“卫生”、纪律”、活动参与”四个方面考核打分,各项满分均为100分,按比例计算综合得分,各项所占比例如表所示:项目 学习 卫生 纪律 活动参与 所占比例 40% 25% 25% 10% 八年级(1)班这四项得分依次为95分,90分,88分,80分,若学校规定班级四项综合得分超过90分的将会获得先进班集体,请你通过计算说明该班是否会获得先进班集体?
21. 某地一楼房发生火灾,消防队员决定用消防车上的云梯救人如图(1).如图(2),已知云梯最多只能伸长到(即),消防车高 , 救人时云梯伸长至最长,在完成从(即)高的处救人后,还要从(即)高的处救人,这时消防车从处向着火的楼房靠近的距离为多少米?(延长交于点 , , 点在上,的长即为消防车的高)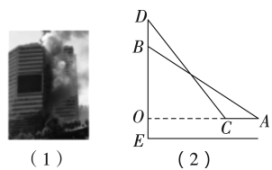 22. 如图,在中,点 , 分别在 , 上,点 , 在上,连接 , , . , .
22. 如图,在中,点 , 分别在 , 上,点 , 在上,连接 , , . , .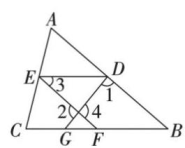 (1)、求证:;(2)、若 , , 求的度数.23. 某居民小区为了改善小区环境,建设和谐家园,准备将一块周长为76米的长方形空地,设计成全等的9块小长方形,如图所示,小长方形的长和宽各是多少米?
(1)、求证:;(2)、若 , , 求的度数.23. 某居民小区为了改善小区环境,建设和谐家园,准备将一块周长为76米的长方形空地,设计成全等的9块小长方形,如图所示,小长方形的长和宽各是多少米?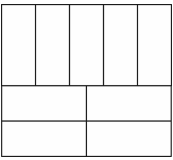 24. 如图,在中,是上一点,若 , , , .
24. 如图,在中,是上一点,若 , , , .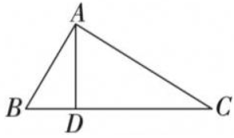 (1)、求证:;(2)、求的面积.25. 某校举办国学知识竞赛,设定满分10分,学生得分均为整数.在初赛中,甲、乙两组(每组10人)学生成绩如下(单位:分)
(1)、求证:;(2)、求的面积.25. 某校举办国学知识竞赛,设定满分10分,学生得分均为整数.在初赛中,甲、乙两组(每组10人)学生成绩如下(单位:分)甲组:5,6,6,6,6,6,7,9,9,10.
乙组:5,6,6,6,7,7,7,7,9,10.
组别
平均数
中位数
众数
方差
甲组
7
6
2.6
乙组
7
(1)、以上成绩统计分析表中 , , ;(2)、小明同学说:“这次竞赛我得了7分,在我们小组中属中游略偏上!”观察上面表格判断,小明可能是组的学生;(3)、从平均数和方差看,若从甲、乙两组学生中选择一个成绩较为稳定的小组参加决赛,应选哪个组?并说明理由.26. 如图,已知函数的图象与轴交于点 , 一次函数的图象经过点 , 与轴以及的图象分别交于点 , , 且点的坐标为.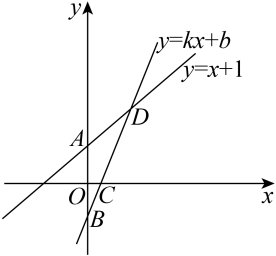 (1)、则 , , ;(2)、关于 , 的二元一次方程组的解为;(3)、求四边形的面积;(4)、在轴上是否存在点 , 使得以点 , , 为顶点的三角形是直角三角形,请求出点的坐标.
(1)、则 , , ;(2)、关于 , 的二元一次方程组的解为;(3)、求四边形的面积;(4)、在轴上是否存在点 , 使得以点 , , 为顶点的三角形是直角三角形,请求出点的坐标.