广西壮族自治区贺州市平桂区2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-02-21 类型:期末考试
一、单选题
-
1. 的值等于( )A、 B、 C、1 D、2. 下列函数中,y是x的反比例函数的是( )A、y= B、y=6x C、x+y=6 D、y=3. 抛物线的顶点坐标是( )A、 B、 C、 D、4. 如果线段 , 那么的值为( )A、 B、 C、 D、25. 如图,在四边形中,与相交于点O,则下列三角形中,与一定相似的是( )
 A、 B、 C、 D、6. 关于二次函数的图象,下列说法正确的是( )A、函数的最大值是2 B、当时,y随x的增大而增大 C、图象的开口向下 D、当时,y随x的增大而增大7. 已知 , 且.若的周长为8,则的周长是( )A、4 B、8 C、12 D、188. 已知二次函数的图象与x轴有交点,则k的取值范围是( )A、且 B、且 C、 D、9. 若点在反比例函数的图象上,则的大小关系是( )A、 B、 C、 D、10. 如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,则sinB的值为( )
A、 B、 C、 D、6. 关于二次函数的图象,下列说法正确的是( )A、函数的最大值是2 B、当时,y随x的增大而增大 C、图象的开口向下 D、当时,y随x的增大而增大7. 已知 , 且.若的周长为8,则的周长是( )A、4 B、8 C、12 D、188. 已知二次函数的图象与x轴有交点,则k的取值范围是( )A、且 B、且 C、 D、9. 若点在反比例函数的图象上,则的大小关系是( )A、 B、 C、 D、10. 如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,则sinB的值为( ) A、 B、 C、 D、11. 如图,正方形中,为上一点, , 交的延长线于点 , 若 , , 则的长为( )
A、 B、 C、 D、11. 如图,正方形中,为上一点, , 交的延长线于点 , 若 , , 则的长为( ) A、 B、 C、 D、12. 如图是二次函数( , , 是常数,)图象的一部分,与轴的交点在点(2,0)和(3,0)之间,对称轴是直线.对于下列说法:①;②;③;④(为实数);⑤当时, , 其中正确的是( )
A、 B、 C、 D、12. 如图是二次函数( , , 是常数,)图象的一部分,与轴的交点在点(2,0)和(3,0)之间,对称轴是直线.对于下列说法:①;②;③;④(为实数);⑤当时, , 其中正确的是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 已知 , 则.14. 二次函数的图像经过点 , 则的值为 .15. 在锐角三角形中, , 则的大小是 .16. 如图,的面积为8,点、分别是、的中点,则四边形的面积为.
 17. 如图,在菱形中, , , , 则菱形的周长为 .
17. 如图,在菱形中, , , , 则菱形的周长为 . 18. 如图所示,反比例函数y= (k≠0,x>0)的图象经过矩形OABC的对角线AC的中点D.若矩形OABC的面积为8,则k的值为
18. 如图所示,反比例函数y= (k≠0,x>0)的图象经过矩形OABC的对角线AC的中点D.若矩形OABC的面积为8,则k的值为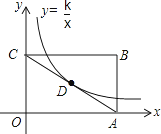
19. 计算:三、解答题
-
20. 如图,在边长均为1的小正方形网格中,以点O为位似中心,将△ABC放大为原来的2倍,得到.
 (1)、请在网格中画出;(2)、直接写出的正弦值.21. 如图,在中,平分 , .若 , , , 求的长.
(1)、请在网格中画出;(2)、直接写出的正弦值.21. 如图,在中,平分 , .若 , , , 求的长. 22. 如图,一次函数的图象与反比例函数()的图象交于 , 两点,点的横坐标为.
22. 如图,一次函数的图象与反比例函数()的图象交于 , 两点,点的横坐标为. (1)、求的值及点的坐标;(2)、根据图象,当时,直接写出的取值范围.23. 一种商品每件售价为10元,一周可卖出50件.市场调查表明:这种商品如果每件涨价1元,每周要少卖5件.已知该商品进价每件为8元,设每件商品售价为x元 , 每周销售的销售利润为y元.(1)、求y与x之间的函数关系式.(2)、问每件商品涨价多少元时,每周销售利润最大,最大利润多少元?24. 如图,四边形是某速滑场馆建造的滑台,已知 , 滑台的高为米,且坡面的坡度为 , 为了提高安全性,负责人决定降低坡度,改造后的新坡面的坡度为.
(1)、求的值及点的坐标;(2)、根据图象,当时,直接写出的取值范围.23. 一种商品每件售价为10元,一周可卖出50件.市场调查表明:这种商品如果每件涨价1元,每周要少卖5件.已知该商品进价每件为8元,设每件商品售价为x元 , 每周销售的销售利润为y元.(1)、求y与x之间的函数关系式.(2)、问每件商品涨价多少元时,每周销售利润最大,最大利润多少元?24. 如图,四边形是某速滑场馆建造的滑台,已知 , 滑台的高为米,且坡面的坡度为 , 为了提高安全性,负责人决定降低坡度,改造后的新坡面的坡度为. (1)、求新坡面的坡角及的长;(2)、原坡面底部的正前方米外(米)是护墙 , 为保证安全,体育管理部门规定,坡面底部至少距护墙米,请问新的设计方案能否通过?请说明理由.(参考数据:)
(1)、求新坡面的坡角及的长;(2)、原坡面底部的正前方米外(米)是护墙 , 为保证安全,体育管理部门规定,坡面底部至少距护墙米,请问新的设计方案能否通过?请说明理由.(参考数据:)

