广西壮族自治区崇左市2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-02-21 类型:期末考试
一、单选题
-
1. 2cos 30°的值等于( )A、 1 B、 C、 D、22. 下列函数中,y是x的反比例函数的是( )
A、 B、 C、y=3x D、y=x23. 已知2x=3y(xy≠0),那么下列比例式中成立的是( )A、 B、 C、 D、4. 已知反比例函数的图象经过点(2,﹣4),那么这个反比例函数的解析式是( )A、y= B、y=﹣ C、y= D、y=﹣5. 已知点、、在反比例函数的图象上,则、、的大小关系是( )A、 B、 C、 D、6. 在△ABC中,∠C=90°,AC=BC,则tanA等于A、 B、1 C、 D、7. 对于二次函数 的图象,下列说法正确的是( )A、开口向上 B、对称轴是x=-3 C、当x>-4 时,y随x的增大而减小 D、顶点坐标为(-2,-3)8. 如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )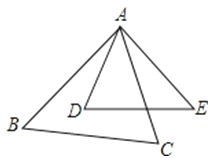 A、= B、= C、= D、=9. 如图,与是位似图形,相似比为 , 已知 , 则的长为( )
A、= B、= C、= D、=9. 如图,与是位似图形,相似比为 , 已知 , 则的长为( ) A、10 B、12 C、14 D、1610. 抛物线的顶点坐标是( )A、 B、 C、 D、11.
A、10 B、12 C、14 D、1610. 抛物线的顶点坐标是( )A、 B、 C、 D、11.如图,在△ABC中,AB=24,AC=18,D是AC上一点,AD=12.在AB上取一点E . 使A、D、E三点组成的三角形与△ABC相似,则AE的长为( ).
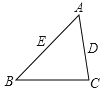 A、16 B、14 C、16或14 D、16或912. 如图,在一笔直的沿湖道路l上有、两个游船码头,观光岛屿在码头北偏东的方向,在码头北偏西的方向,.游客小张准备从观光岛屿乘船沿回到码头或沿回到码头 , 设开往码头、的游船速度分别为、 , 若回到、所用时间相等,则( )
A、16 B、14 C、16或14 D、16或912. 如图,在一笔直的沿湖道路l上有、两个游船码头,观光岛屿在码头北偏东的方向,在码头北偏西的方向,.游客小张准备从观光岛屿乘船沿回到码头或沿回到码头 , 设开往码头、的游船速度分别为、 , 若回到、所用时间相等,则( ) A、 B、 C、4 D、6
A、 B、 C、4 D、6二、填空题
-
13. 函数是二次函数,则.14. 如图, ,相似比为 ,则面积之比 为 .
 15. 抛物线如图所示,利用图象可得方程的近似解为(精确到0.1).
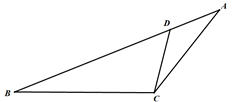
15. 抛物线如图所示,利用图象可得方程的近似解为(精确到0.1).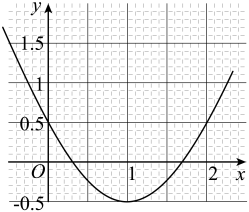 16. 在中,若 , , 都是锐角,则是三角形.17. 如图,、交于点 , 且 , , , 当时,与相似.
16. 在中,若 , , 都是锐角,则是三角形.17. 如图,、交于点 , 且 , , , 当时,与相似. 18. 如图,点为直线上的两点,过两点分别作轴的平行线交双曲线于点 , 若 , 则的值为.
18. 如图,点为直线上的两点,过两点分别作轴的平行线交双曲线于点 , 若 , 则的值为.
三、解答题
-
19. 计算:4sin30°﹣ cos45°+tan260°.20. 如图,在平面直角坐标系中,的顶点坐标分别为 , , .
 (1)、请以原点为位似中心,画出 , 使它与的相似比为;(2)、若图形变换后点、的对应点分别为点、 , 请直接写出点、点的坐标.21. 如图,一次函数的图象与反比例函数的图象相交于和两点.
(1)、请以原点为位似中心,画出 , 使它与的相似比为;(2)、若图形变换后点、的对应点分别为点、 , 请直接写出点、点的坐标.21. 如图,一次函数的图象与反比例函数的图象相交于和两点. (1)、求反比例函数的解析式;(2)、求点的坐标.(3)、根据图象直接写出不等式的解集.22. 全球最长跨海大桥——港珠澳大桥连接香港、澳门、珠海三地,总长55千米.大桥某段采用低塔斜拉桥桥型,图2是从图1引申出的平面图.假设你站在桥上测得拉索与水平桥面的夹角是 , 拉索与水平桥面的夹角是 , 两拉索顶端的距离为2米,两拉索底端距离为20米,请求出立柱的长.(结果精确到0.1米,).
(1)、求反比例函数的解析式;(2)、求点的坐标.(3)、根据图象直接写出不等式的解集.22. 全球最长跨海大桥——港珠澳大桥连接香港、澳门、珠海三地,总长55千米.大桥某段采用低塔斜拉桥桥型,图2是从图1引申出的平面图.假设你站在桥上测得拉索与水平桥面的夹角是 , 拉索与水平桥面的夹角是 , 两拉索顶端的距离为2米,两拉索底端距离为20米,请求出立柱的长.(结果精确到0.1米,). 23. 如图,将矩形纸片沿着过点的直线折叠,使点A落在边上,落点为 , 折痕交边于点.
23. 如图,将矩形纸片沿着过点的直线折叠,使点A落在边上,落点为 , 折痕交边于点. (1)、若 , , 求的值;(2)、若 , , 求的长.24. 为了有效预防和控制疫情,及时监测疫情发展态势,实施定期核酸检测.某社区准备搭建一个动态核酸检测点,现有33米可移动的隔离带,围成如图的临时检测点,这是一个一面靠墙(墙面为)的矩形,内部分成两个区,区为登记区,区为检测区,入口通道在边上,两区通道在边上,出口通道在边上,通道宽均为1米.设 , 矩形的面积为.
(1)、若 , , 求的值;(2)、若 , , 求的长.24. 为了有效预防和控制疫情,及时监测疫情发展态势,实施定期核酸检测.某社区准备搭建一个动态核酸检测点,现有33米可移动的隔离带,围成如图的临时检测点,这是一个一面靠墙(墙面为)的矩形,内部分成两个区,区为登记区,区为检测区,入口通道在边上,两区通道在边上,出口通道在边上,通道宽均为1米.设 , 矩形的面积为. (1)、可表示为;(2)、当为何值时,有最大值?最大值是多少?(3)、所围成矩形的面积能否达到96平方米?如果能,求出的长;如果不能,请说明理由.
(1)、可表示为;(2)、当为何值时,有最大值?最大值是多少?(3)、所围成矩形的面积能否达到96平方米?如果能,求出的长;如果不能,请说明理由.

