陕西省西安市雁塔二中2021-2022学年八年级下学期第一次月考数学试卷
试卷更新日期:2023-02-21 类型:月考试卷
一、单选题
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知 , 下列不等式中,不正确的是( )A、 B、 C、 D、3. 下列各组线段、、中能组成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 如图,已知平分 , 是上一点,于点 , 是射线上的一个动点,如 , 则长的最小值为( )
2. 已知 , 下列不等式中,不正确的是( )A、 B、 C、 D、3. 下列各组线段、、中能组成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 如图,已知平分 , 是上一点,于点 , 是射线上的一个动点,如 , 则长的最小值为( ) A、10 B、5 C、3 D、2.55. 在平面直角坐标系内,将点M(5,2)先向下平移2个单位,再向左平移3个单位,则移动后的点的坐标是( )A、(2,3) B、(2,0) C、(3,5) D、(8,4)6. 在联欢会上,有、、三名选手站在一个三角形的三个顶点位置上,他们在玩“抢凳子”游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子最适当的位置应放在的( )A、三边垂直平分线的交点 B、三条中线的交点 C、三条角平分线的交点 D、三条高所在直线的交点7. 如图,直线y=kx+b与直线y=3x-2相交于点( , -),则不等式3x-2<kx+b的解为( )
A、10 B、5 C、3 D、2.55. 在平面直角坐标系内,将点M(5,2)先向下平移2个单位,再向左平移3个单位,则移动后的点的坐标是( )A、(2,3) B、(2,0) C、(3,5) D、(8,4)6. 在联欢会上,有、、三名选手站在一个三角形的三个顶点位置上,他们在玩“抢凳子”游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子最适当的位置应放在的( )A、三边垂直平分线的交点 B、三条中线的交点 C、三条角平分线的交点 D、三条高所在直线的交点7. 如图,直线y=kx+b与直线y=3x-2相交于点( , -),则不等式3x-2<kx+b的解为( ) A、x> B、x< C、x>- D、x<-8. 如果不等式组 有解,那么m的取值范围是( )A、m>5 B、m≥5 C、m<5 D、m≤89. 如图,在等边三角形中,是边上一点,连接 , 将绕点逆时针旋转 , 得到 , 连接 , 若 , , 则下列结论错误的是( )
A、x> B、x< C、x>- D、x<-8. 如果不等式组 有解,那么m的取值范围是( )A、m>5 B、m≥5 C、m<5 D、m≤89. 如图,在等边三角形中,是边上一点,连接 , 将绕点逆时针旋转 , 得到 , 连接 , 若 , , 则下列结论错误的是( ) A、 B、是等边三角形 C、 D、的周长是
A、 B、是等边三角形 C、 D、的周长是二、填空题
-
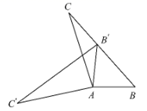
10. 根据数量关系:的倍与的差不大于2,可列不等式.11. 请写出“对顶角相等”这一命题的逆命题.12. 如果等腰三角形的一腰上的高等于腰长的一半,则其一个底角的度数是 .13. 如图,在 中, ,将 绕点 按逆时针方向旋转得到 .若点 恰好落在 边上,且 ,则 的度数为 .
三、解答题
-
14. 解不等式 , 并把它们的解集在数轴上表示出来.
 15. 解不等式组 , 并求出该不等式组的整数解.16. 已知:如图,是的高,且.求证:是等腰三角形.
15. 解不等式组 , 并求出该不等式组的整数解.16. 已知:如图,是的高,且.求证:是等腰三角形. 17. 如图所示,三个顶点的坐标分别为 , , .
17. 如图所示,三个顶点的坐标分别为 , , .
⑴画出向右平移5个单位长度后得到的图形 , 并写出的坐标.
⑵画出以点为旋转中心旋转后得到的图形 , 并写出的坐标.
18. 如图,在中,的垂直平分线分别交于点D,E.求证:.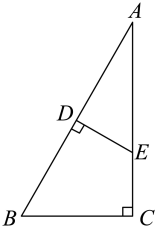 19. 如图,已知直线,与轴交于点 , 直线与轴交于点 , 且与直线交于第二象限点若的面积为.
19. 如图,已知直线,与轴交于点 , 直线与轴交于点 , 且与直线交于第二象限点若的面积为. (1)、求点、点的坐标;(2)、写出关于的不等式的解集.20. 如图,在中, , , 边上的中线 , 求的长.
(1)、求点、点的坐标;(2)、写出关于的不等式的解集.20. 如图,在中, , , 边上的中线 , 求的长. 21. 如图,△ABC中,AD平分 , 且平分BC,于E,于F.
21. 如图,△ABC中,AD平分 , 且平分BC,于E,于F. (1)、证明:;(2)、如果 , , 求AE、BE的长.22. 某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为4000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一台按原价收费,其余每台优惠25%;乙商场的优惠条件是:每台优惠20%.(1)、设该学校所买的电脑台数是x台,选择甲商场时,所需费用为元,选择乙商场时,所需费用为元,请分别写出 , 与x之间的关系式;(2)、该学校如何根据所买电脑的台数选择到哪间商场购买,所需费用较少?23. 如图
(1)、证明:;(2)、如果 , , 求AE、BE的长.22. 某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为4000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一台按原价收费,其余每台优惠25%;乙商场的优惠条件是:每台优惠20%.(1)、设该学校所买的电脑台数是x台,选择甲商场时,所需费用为元,选择乙商场时,所需费用为元,请分别写出 , 与x之间的关系式;(2)、该学校如何根据所买电脑的台数选择到哪间商场购买,所需费用较少?23. 如图 (1)、如图1,与均是顶角为的等腰三角形,分别是底边,求证:;(2)、如图2,和均为等边三角形,点在同一直线上,连接 .
(1)、如图1,与均是顶角为的等腰三角形,分别是底边,求证:;(2)、如图2,和均为等边三角形,点在同一直线上,连接 .填空:的度数为;线段与之间的数量关系是 .
(3)、拓展探究如图3,和均为等腰直角三角形, , 点在同一直线上,为中边上的高,连接 . 请判断的度数及线段、、之间的数量关系,并说明理由.