陕西省宝鸡市凤翔县2021-2022学年七年级下学期第一次月考数学试卷

试卷更新日期：2023-02-21 类型：月考试卷

进入出卷网下载

一、单选题

1. 化简： $(- x)^{3} \cdot (- x^{2})$ 的结果为（）

A、 $x^{5}$ B、 $x^{6}$ C、 $- x^{5}$ D、 $- x^{6}$

查看试题解析
2. 下列运算正确的是（）

A、 $a^{4} + a^{5} = a^{9}$ B、 $a^{3} \cdot a^{3} \cdot a^{3} = 3 a^{3}$ C、 $2 a^{4} \times 3 a^{5} = 6 a^{9}$ D、 $(- a^{3})^{4} = a^{7}$

查看试题解析
3. 生物学家发现了一种病毒，其长度约为0.00000032mm，数据0.00000032用科学记数法表示正确的是（　　）

A、3.2×10⁷ B、3.2×10⁸ C、3.2×10^-7 D、3.2×10^-8

查看试题解析
4. 在下列计算中，不能用平方差公式计算的是（）

A、 $(m - n) (- m + n)$ B、 $(x^{3} - y^{3}) (x^{3} + y^{3})$ C、 $(- a - b) (a - b)$ D、 $(c^{2} - d^{2}) (d^{2} + c^{2})$

查看试题解析
5. 已知 $x + y = 4$ ， $x y = 3$ ，则 $x^{2} + y^{2}$ 的值为（）

A、22 B、16 C、10 D、4

查看试题解析
6. 已知多项式 $x - a$ 与 $x^{2} + 2 x - 1$ 的乘积中不含 $x^{2}$ 项，则常数a的值是（）

A、-1 B、1 C、-2 D、2

查看试题解析
7. 计算 $3 n \cdot (- 9) \cdot 3 n^{2}$ 的结果是（）

A、 $- 3^{3} n^{2}$ B、 $- 3 n^{4}$ C、 $- 3^{4} n^{3}$ D、 $- 3 n^{6}$

查看试题解析
8.
如图，甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式： ①（2a+b）（m+n）； ②2a（m+n）+b（m+n）；
③m（2a+b）+n（2a+b）；　④2am+2an+bm+bn，你认为其中正确的有（　　）

A、①② B、③④ C、①②③ D、①②③④

查看试题解析
9. 下列说法中正确的有（）
①在同一平面内，不重合的两条直线若不相交，则必平行；②在同一平面内，不相交的两条线段必平行；③相等的角是对顶角；④两条直线被第三条直线所截，所得的同位角相等；⑤两条平行线被第三条直线所截，一对内错角的角平分线互相平行.

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，在△ABC中， $∠ C = 90 °$ ， AD是∠BAC的平分线，若 $∠ A D C = 65 °$ ，则∠BAC的大小为（）

A、35° B、50° C、65° D、70°

查看试题解析

二、填空题

11. 计算: ${(\frac{3}{4})}^{2017} \times {(- 1 \frac{1}{3})}^{2018} =$ .

查看试题解析
12. 已知 $M = (x - 2) (x - 6)$ ， $N = (x - 5) (x - 3)$ ，则 $M$ 与 $N$ 的大小关系是．

查看试题解析
13. 已知 $x^{2} - k x + 16$ 是完全平方式，则 $k =$ .

查看试题解析
14. 已知a＋ $\frac{1}{a}$ ＝5，则a²＋ $\frac{1}{a^{2}}$ 的结果是．

查看试题解析
15.
通过计算几何图形的面积可表示一些代数恒等式（一定成立的等式），请根据图写出一个代数恒等式是：．

查看试题解析
16. 若 $m^{2} - n^{2} = - 6$ ，且m-n＝-3，则m+n＝.

查看试题解析
17. 如图，体育课上老师测量跳远的成绩是这样操作的：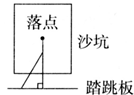
用一块直角三角尺的一边附在踏跳板上，另一边与拉直的皮尺重合，并且使皮尺经过被测试同学的落点，这样做的理由是.

查看试题解析
18. 计算：（1﹣ $\frac{1}{2^{2}}$ ）（1﹣ $\frac{1}{3^{2}}$ ）（1﹣ $\frac{1}{4^{2}}$ ）…（1﹣ $\frac{1}{100^{2}}$ ）＝.

查看试题解析

三、解答题

19. 计算.

(1)、 $(- 1)^{2012} + (- \frac{1}{2})^{- 2} - (3.14 - π)^{0}$ ；

(2)、 $(6 m^{2} n - 6 m^{2} n^{2} - 3 m^{2}) \div (- 3 m^{2}) .$

查看试题解析
20. 运用乘法公式简便计算：

(1)、9997 ²

(2)、 $118 6^{2} - 1185 \times 1187$

查看试题解析
21. 计算.

(1)、 $(x + 3 y - 2) (x - 3 y - 2)$ ；

(2)、 $(x + 4)^{2} - (x + 2) (x - 5)$ ；

(3)、 $(3 a b + 4)^{2} - (3 a b - 4)^{2}$ .

查看试题解析
22. 先化简，再求值： $x (x - 4 y) + (2 x + y) (2 x - y) - {(2 x - y)}^{2}$ ，其中 $x = - 2$ ， $y = - \frac{1}{2}$ ．

查看试题解析
23.

(1)、已知4m+n=90，2m-3n=10，求（m+2n）²-（3m-n）²的值

(2)、已知（a+b）²=7，ab=2，求a²+b²值

查看试题解析
24. 如图，某市有一块长为（3a+b）米，宽为（2a+b）米的长方形地块，规划部门计划将阴影部分进行绿化，中间将修建一座雕像．

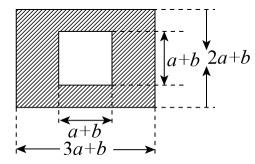(1)、绿化的面积是多少平方米？

(2)、并求出当a=3，b=2时的绿化面积．

查看试题解析
25. 如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘数”.如， $4 = 2^{2} - 0$ ， $12 = 4^{2} - 2^{2} ， 20 = 6^{2} - 4^{2}$ ，因此4，12，20这三个数都是神秘数.

(1)、28和2012这两个数是神秘数吗?为什么?

(2)、设两个连续偶数为 $2 k + 2$ 和 $2 k$ （其中k取非负整数），由这两个连续偶数构造的神秘数是4的倍数吗?为什么?

(3)、两个连续奇数的平方差（取正数）是神秘数吗?为什么?

查看试题解析
26. 如图1， $C E$ 平分 $∠ A C D$ ， $A E$ 平分 $∠ B A C$ ， $∠ E A C + ∠ A C E = 90 °$

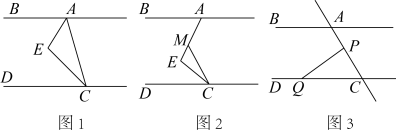(1)、请判断 $A B$ 与 $C D$ 的位置关系并说明理由；

(2)、如图2，在（1）的结论下，当 $∠ E = 90 °$ 保持不变，移动直角顶点E，使 $∠ M C E = ∠ E C D$ ，当直角顶点E点移动时，问 $∠ B A E$ 与 $∠ M C D$ 是否存在确定的数量关系？

(3)、如图3，在（1）的结论下，P为线段 $A C$ 上一定点，点Q为直线 $C D$ 上一动点，当点Q在射线 $C D$ 上运动时（点C除外）， $∠ C P Q + ∠ C Q P$ 与 $∠ B A C$ 有何数量关系？

查看试题解析