广东省深圳市龙岗区2022-2023学年高一上学期数学期末试卷
试卷更新日期:2023-02-20 类型:期末考试
一、单选题
-
1. 命题:“ ”的否定是( )A、 B、 C、 D、2. 的值是( )A、 B、 C、 D、3. 集合 , 是自然数集,则( )A、 B、 C、 D、4. 设 , 则是的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 当时,在同一平面直角坐标系中,与的图象是( )A、
 B、
B、 C、
C、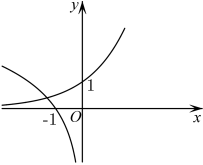 D、
D、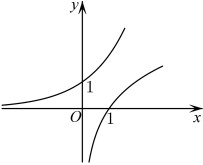 6. 将函数图象上各点的横坐标伸长到原来的2倍,再向左平移个单位,纵坐标不变,所得函数图象的一条对称轴的方程是( )A、 B、 C、 D、7. 设实数 满足 ,函数 的最小值为( )A、 B、 C、 D、68. 酒驾是严重危害交通安全的违法行为.根据国家有关规定:驾驶人血液中的酒精含量大于(或等于)毫克/毫升,小于毫克/毫升的情况下驾驶机动车属于饮酒驾车;含量大于(或等于)毫克/毫升的情况下驾驶机动车属于醉酒驾车.假设某驾驶员一天晚上点钟喝了一定量的酒后,其血液中酒精含量上升到毫克/毫升.如果在停止喝酒后,他血液中酒精含量以每小时的速度减少,则他次日上午最早( )点(结果取整数)开车才不构成酒驾.(参考数据: , )A、 B、 C、 D、
6. 将函数图象上各点的横坐标伸长到原来的2倍,再向左平移个单位,纵坐标不变,所得函数图象的一条对称轴的方程是( )A、 B、 C、 D、7. 设实数 满足 ,函数 的最小值为( )A、 B、 C、 D、68. 酒驾是严重危害交通安全的违法行为.根据国家有关规定:驾驶人血液中的酒精含量大于(或等于)毫克/毫升,小于毫克/毫升的情况下驾驶机动车属于饮酒驾车;含量大于(或等于)毫克/毫升的情况下驾驶机动车属于醉酒驾车.假设某驾驶员一天晚上点钟喝了一定量的酒后,其血液中酒精含量上升到毫克/毫升.如果在停止喝酒后,他血液中酒精含量以每小时的速度减少,则他次日上午最早( )点(结果取整数)开车才不构成酒驾.(参考数据: , )A、 B、 C、 D、二、多选题
-
9. 若 ,则下列不等式正确的是( )A、 B、 C、 D、10. 已知函数 , 则以下结论正确的是( )A、 B、函数是定义域上的增函数 C、函数有个零点 D、方程有两个实数解11. 函数在区间上单调递增,则的取值可能为( )A、 B、 C、 D、12. 已知函数 , 下列说法中正确的是( )A、若的定义域为R,则 B、若的值域为R,则或 C、若 , 则的单调减区间为 D、若在上单调递减,则
三、填空题
-
13. 若扇形的面积为9,圆心角为2弧度,则该扇形的弧长为 .14. 已知是定义在上的奇函数, 当时, , 则的值为.15. 若 , 则 .16. 若存在常数和 , 使得函数和对其公共定义域上的任意实数满足:和恒成立,则称此直线为和的“隔离直线”.已知函数 , , 若函数和之间存在隔离直线 , 则实数的取值范围是.
四、解答题
-
17. 设 , 已知集合 , .(1)、当时,求;(2)、若 , 且 , 求实数的取值范围.18. 函数的定义域为A.(1)、求A;(2)、若函数在A上是单调函数,求实数的取值范围.19. 已知函数的部分图象如图所示,其中的图像与轴的一个交点的横坐标为.
 (1)、求这个函数的解析式,并写出它的递增区间;(2)、求函数在区间上的最大值和最小值.20. 已知定义在上的函数为奇函数.(1)、求的值,试判断的单调性,并用定义证明;(2)、若 , 求的取值范围.21. 济南市地铁项目正在加火如荼的进行中,通车后将给市民出行带来便利,已知某条线路通车后,列车的发车时间间隔t(单位:分钟)满足 , 经市场调研测算,列车载客量与发车时间间隔t相关,当时列车为满载状态,载客量为500人,当时,载客量会减少,减少的人数与的平方成正比,且发车时间间隔为2分钟时的载客量为372人,记列车载客量为.(1)、求的表达式,并求当发车时间间隔为5分钟时,列车的载客量;(2)、若该线路每分钟的净收益为(元),问当发车时间间隔为多少时,该线路每分钟的净收益最大,并求出最大值.22. 已知常数 , 函数.(1)、当时,求不等式的解集(用区间表示);(2)、若函数有两个零点,求的取值范围;(3)、设a>0,若对任意t∈[-1,0],函数f(x)在区间[t,t+1]上的最大值与最小值的和不大于log26,求a的取值范围.
(1)、求这个函数的解析式,并写出它的递增区间;(2)、求函数在区间上的最大值和最小值.20. 已知定义在上的函数为奇函数.(1)、求的值,试判断的单调性,并用定义证明;(2)、若 , 求的取值范围.21. 济南市地铁项目正在加火如荼的进行中,通车后将给市民出行带来便利,已知某条线路通车后,列车的发车时间间隔t(单位:分钟)满足 , 经市场调研测算,列车载客量与发车时间间隔t相关,当时列车为满载状态,载客量为500人,当时,载客量会减少,减少的人数与的平方成正比,且发车时间间隔为2分钟时的载客量为372人,记列车载客量为.(1)、求的表达式,并求当发车时间间隔为5分钟时,列车的载客量;(2)、若该线路每分钟的净收益为(元),问当发车时间间隔为多少时,该线路每分钟的净收益最大,并求出最大值.22. 已知常数 , 函数.(1)、当时,求不等式的解集(用区间表示);(2)、若函数有两个零点,求的取值范围;(3)、设a>0,若对任意t∈[-1,0],函数f(x)在区间[t,t+1]上的最大值与最小值的和不大于log26,求a的取值范围.