江苏省南通市2023届高三下学期数学第一次调研测试试卷

试卷更新日期：2023-02-20 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x ∣ 1 \leq x \leq 3} ， B = {x ∣ 2 < x < 4}$ ，则 $A ∩ B =$ （）

A、 $(2 ， 3]$ B、 $[1 ， 4)$ C、 $(- \infty ， 4)$ D、 $[1 ， + \infty)$

查看试题解析
2. 已知向量 $\vec{a} ， \vec{b}$ 满足 $| \vec{a} | = 1 ， | \vec{b} | = 2 ， ⟨ \vec{a} ， \vec{b} ⟩ = \frac{2 π}{3}$ ，则 $\vec{a} \cdot (\vec{a} + \vec{b}) =$ （）

A、-2 B、-1 C、0 D、2

查看试题解析
3. 在复平面内，复数 $z_{1} ， z_{2}$ 对应的点关于直线 $x - y = 0$ 对称，若 $z_{1} = 1 - i$ ，则 $| z_{1} - z_{2} | =$ （）

A、 $\sqrt{2}$ B、2 C、 $2 \sqrt{2}$ D、4

查看试题解析
4. 2022年神舟接力腾飞，中国空间站全面建成，我们的“太空之家”遨游苍穹.太空中飞船与空间站的对接，需要经过多次变轨.某飞船升空后的初始运行轨道是以地球的中心为一个焦点的椭圆，其远地点（长轴端点中离地面最远的点）距地面 $S_{1}$ ，近地点（长轴端点中离地面最近的点）距地面 $S_{2}$ ，地球的半径为 $R$ ，则该椭圆的短轴长为（）

A、 $\sqrt{S_{1} S_{2}}$ B、 $2 \sqrt{S_{1} S_{2}}$ C、 $\sqrt{(S_{1} + R) (S_{2} + R)}$ D、 $2 \sqrt{(S_{1} + R) (S_{2} + R)}$

查看试题解析
5. 已知 $s i n (α - \frac{π}{6}) + c o s α = \frac{3}{5}$ ，则 $c o s (2 α + \frac{π}{3}) =$ （）

A、 $- \frac{7}{25}$ B、 $\frac{7}{25}$ C、 $- \frac{24}{25}$ D、 $\frac{24}{25}$

查看试题解析
6. 已知随机变量 $X$ 服从正态分布 $N (μ ， σ^{2})$ ，有下列四个命题：
甲： $P (X > m + 1) > P (X < m - 2)$ ；
乙： $P (X > m) = 0.5$ ；
丙： $P (X \leq m) = 0.5$ ；
丁： $P (m - 1 < X < m) < P (m + 1 < X < m + 2)$
如果只有一个假命题，则该命题为（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
7. 已知函数 $f (x)$ 的定义域为 $R$ ，且 $f (2 x + 1)$ 为偶函数， $f (x) = f (x + 1) - f (x + 2)$ ，若 $f (1) = 2$ ，则 $f (18) =$ （）

A、1 B、2 C、 $- 1$ D、 $- 2$

查看试题解析
8. 若过点 $P (t ， 0)$ 可以作曲线 $y = (1 - x) e^{x}$ 的两条切线，切点分别为 $A (x_{1} ， y_{1}) ， B (x_{2} ， y_{2})$ ，则 $y_{1} y_{2}$ 的取值范围是（）

A、 $(0 ， 4 e^{- 3})$ B、 $(- ∞ ， 0) \cup (0 ， 4 e^{- 3})$ C、 $(- ∞ ， 4 e^{- 2})$ D、 $(- ∞ ， 0) \cup (0 ， 4 e^{- 2})$

查看试题解析

二、多选题

9. 在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A C$ 与 $B D$ 交于点 $O$ ，则（）

A、 $A D_{1}$ $/ /$ 平面 $B O C_{1}$ B、 $B D ⊥$ 平面 $C O C_{1}$ C、 $C_{1} O$ 与平面 $A B C D$ 所成的角为 $4 5^{∘}$ D、三棱锥 $C - B O C_{1}$ 的体积为 $\frac{2}{3}$

查看试题解析
10. 函数 $f (x) = s i n (ω x + φ) (ω > 0 ， | φ | < \frac{π}{2})$ 的部分图象如图所示，则（）

A、 $ω = 2$ B、 $φ = \frac{π}{6}$ C、 $f (x)$ 的图象关于点 $(\frac{π}{12} ， 0)$ 对称 D、 $f (x)$ 在区间 $(π ， \frac{5 π}{4})$ 上单调递增

查看试题解析
11. 一个袋中有大小､形状完全相同的3个小球，颜色分别为红､黄､蓝，从袋中先后无放回地取出2个球，记“第一次取到红球”为事件A，“第二次取到黄球”为事件 $B$ ，则（）

A、 $P (A) = \frac{1}{3}$ B、 $A ， B$ 为互斥事件 C、 $P (B ∣ A) = \frac{1}{2}$ D、 $A ， B$ 相互独立

查看试题解析
12. 已知抛物线 $x^{2} = 4 y$ 的焦点为 $F$ ，以该抛物线上三点 $A ， B ， C$ 为切点的切线分别是 $l_{1} ， l_{2} ， l_{3}$ ，直线 $l_{1} ， l_{2}$ 相交于点 $D ， l_{3}$ 与 $l_{1} ， l_{2}$ 分别相交于点 $P ， Q$ .记 $A ， B ， D$ 的横坐标分别为 $x_{1} ， x_{2} ， x_{3}$ ，则（）

A、 $\vec{D A} \cdot \vec{D B} = 0$ B、 $x_{1} + x_{2} = 2 x_{3}$ C、 $| A F | \cdot | B F | = | D F |^{2}$ D、 $| A P | \cdot | C Q | = | P C | \cdot | P D |$

查看试题解析

三、填空题

13. 已知函数 $f (x) = {\begin{array}{l} 1 + l o g_{2} (2 - x) ， x < 1 \\ 2^{x - 1} ， x \geq 1 \end{array}$ ，则 $f (f (- 2)) =$ .

查看试题解析
14. 写出一个同时满足下列条件①②的等比数列 ${a_{n}}$ 的通项公式 $a_{n} =$ .
① $a_{n} a_{n + 1} < 0$ ；② $| a_{n} | < | a_{n + 1} |$

查看试题解析
15. 已知圆 $O ： x^{2} + y^{2} = r^{2} (r > 0)$ ，设直线 $x + \sqrt{3} y - \sqrt{3} = 0$ 与两坐标轴的交点分别为 $A ， B$ ，若圆 $O$ 上有且只有一个点 $P$ 满足 $| A P | = | B P |$ ，则 $r$ 的值为.

查看试题解析
16. 已知正四棱锥 $S - A B C D$ 的所有棱长都为1，点 $E$ 在侧棱 $S C$ 上，过点 $E$ 且垂直于 $S C$ 的平面截该棱锥，得到截面多边形 $Γ$ ，则 $Γ$ 的边数至多为， $Γ$ 的面积的最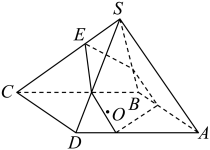大值为.

查看试题解析

四、解答题

17. 在① $S_{1} ， S_{2} ， S_{4}$ 成等比数列，② $a_{4} = 2 a_{2} + 2$ ， ③ $S_{8} = S_{4} + S_{7} - 2$ 这三个条件中任选两个，补充在下面问题中，并完成解答.
已知数列 ${a_{n}}$ 是公差不为0的等差数列，其前 $n$ 项和为 $S_{n}$ ，且满足____，____.
注：如果选择多个方案分别解答，按第一个方案计分.

(1)、求 ${a_{n}}$ 的通项公式；

(2)、求 $\frac{1}{a_{1} a_{2}} + \frac{1}{a_{2} a_{3}} + \frac{1}{a_{3} a_{4}} + ⋯ + \frac{1}{a_{n} a_{n + 1}}$ .

查看试题解析
18. 第二十二届卡塔尔世界杯足球赛（FIFAWorldCupQatar2022）决赛中，阿根廷队通过扣人心弦的点球大战战胜了法国队.某校为了丰富学生课余生活，组建了足球社团.足球社团为了解学生喜欢足球是否与性别有关，随机抽取了男､女同学各100名进行调查，部分数据如表所示：

喜欢足球
不喜欢足球
合计
男生
40
女生
30
合计
附： $K^{2} = \frac{n (a d - b c)^{2}}{(a + b) (c + d) (a + c) (b + d)}$ .
$P (K^{2} \geq k)$
$0.050$
$0.010$
$0.001$
$k$
$3.841$
$6.635$
$10.828$

(1)、根据所给数据完成上表，并判断是否有 $99.9 %$ 的把握认为该校学生喜欢足球与性别有关？

(2)、社团指导老师从喜欢足球的学生中抽取了2名男生和1名女生示范点球射门.已知男生进球的概率为 $\frac{2}{3}$ ，女生进球的概率为 $\frac{1}{2}$ ，每人射门一次，假设各人射门相互独立，求3人进球总次数的分布列和数学期望.

查看试题解析
19. 在 $△ A B C$ 中， $A ， B ， C$ 的对边分别为 $a ， b ， c ， a c o s B - 2 a c o s C = (2 c - b) c o s A$ .

(1)、若 $c = \sqrt{3} a$ ，求 $c o s B$ 的值；

(2)、若 $b = 1 ， ∠ B A C$ 的平分线 $A D$ 交 $B C$ 于点 $D$ ，求 $A D$ 长度的取值范围.

查看试题解析
20. 如图，在 $△ A B C$ 中， $A D$ 是 $B C$ 边上的高，以 $A D$ 为折痕，将 $△ A C D$ 折至 $△ A P D$ 的位置，使得 $P B ⊥ A B$ .

(1)、证明： $P B ⊥$ 平面 $A B D$ ；

(2)、若 $A D = P B = 4 ， B D = 2$ ，求二面角 $B - P A - D$ 的正弦值.

查看试题解析
21. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左顶点为 $A$ ，过左焦点 $F$ 的直线与 $C$ 交于 $P ， Q$ 两点.当 $P Q ⊥ x$ 轴时， $| P A | = \sqrt{10}$ ， $△ P A Q$ 的面积为3.

(1)、求 $C$ 的方程；

(2)、证明：以 $P Q$ 为直径的圆经过定点.

查看试题解析
22. 已知函数 $f (x) = \frac{x}{a e^{x - 1}}$ 和 $g (x) = \frac{a + l n x}{x}$ 有相同的最大值.

(1)、求实数 $a$ ；

(2)、设直线 $y = b$ 与两条曲线 $y = f (x)$ 和 $y = g (x)$ 共有四个不同的交点，其横坐标分别为 $x_{1} ， x_{2} ， x_{3} ， x_{4} (x_{1} < x_{2} < x_{3} < x_{4})$ ，证明： $x_{1} x_{4} = x_{2} x_{3}$ .

查看试题解析

$P (K^{2} \geq k)$	$0.050$	$0.010$	$0.001$
$k$	$3.841$	$6.635$	$10.828$

	喜欢足球	不喜欢足球	合计
男生		40
女生	30
合计