河北省石家庄市2023届高三数学新高考考前模拟试卷
试卷更新日期:2023-02-20 类型:高考模拟
一、单选题
-
1. 设集合 , , 则( )A、 B、 C、 D、2. 已知命题: , , 则为( )A、 , B、 , C、 , D、 ,3. 已知是虚数单位,若复数满足: , 则复数( )A、 B、 C、 D、4. 已知函数 ,且,则下列陈述不正确的是( )A、函数的最小正周期为 B、为的一个对称轴 C、函数在区间上单调 D、函数在区间上有两个零点5. 战国时期的铜镞是一种兵器,其由两部分组成,前段是高为3cm、底面边长为2cm的正三棱锥,后段是高为1cm的圆柱,圆柱底面圆与正三棱锥底面的正三角形内切,则此铜镞的体积为( )
 A、 B、 C、 D、6. 设是双曲线的左,右焦点,过的直线交双曲线的左支于两点,若的最小值为 , 则双曲线的离心率为( )A、 B、 C、 D、7. 甲口袋中有3个红球,2个白球和5个黑球,乙口袋中有3个红球,3个白球和4个黑球,先从甲口袋中随机取出一球放入乙口袋,分别以和表示由甲口袋取出的球是红球,白球和黑球的事件;再从乙口袋中随机取出一球,以B表示由乙口袋取出的球是红球的事件,则下列结论中正确的是( )A、 B、事件与事件B相互独立 C、 D、8. 设函数定义域为 , 为奇函数,为偶函数,当时, , 则下列结论错误的是( )A、 B、为奇函数 C、在上是减函数 D、方程仅有6个实数解
A、 B、 C、 D、6. 设是双曲线的左,右焦点,过的直线交双曲线的左支于两点,若的最小值为 , 则双曲线的离心率为( )A、 B、 C、 D、7. 甲口袋中有3个红球,2个白球和5个黑球,乙口袋中有3个红球,3个白球和4个黑球,先从甲口袋中随机取出一球放入乙口袋,分别以和表示由甲口袋取出的球是红球,白球和黑球的事件;再从乙口袋中随机取出一球,以B表示由乙口袋取出的球是红球的事件,则下列结论中正确的是( )A、 B、事件与事件B相互独立 C、 D、8. 设函数定义域为 , 为奇函数,为偶函数,当时, , 则下列结论错误的是( )A、 B、为奇函数 C、在上是减函数 D、方程仅有6个实数解二、多选题
-
9. 中国网络文学历经20年的发展,取得了引人注目的成就.以往反响较大的玄幻类题材影响力开始下降,讴歌祖国、讴歌人民和英雄、传承优秀传统文化、颂扬当代美好生活的优秀作品逐渐赢得读者的青睐﹐下图是2013—2019年中国网络文学市场规模情况,则下列结论错误的是( )
 A、这7年网络文学市场规模的中位数为 B、2013年至2015年的同比增长相对2017年至2019年,波动性更大 C、这7年网络文学市场规模的极差为 D、这7年同比增长的平均数超过10. 设是两个非零向量,则下列命题中正确的有( )A、若 , 则存在实数使得 B、若 , 则 C、若 , 则在方向上的投影向量为 D、若存在实数使得 , 则11. 如图所示,设单位圆与轴的正半轴相交于点 , 以轴非负半轴为始边作锐角 , , , 它们的终边分别与单位圆相交于点 , , , 则下列说法正确的是( )
A、这7年网络文学市场规模的中位数为 B、2013年至2015年的同比增长相对2017年至2019年,波动性更大 C、这7年网络文学市场规模的极差为 D、这7年同比增长的平均数超过10. 设是两个非零向量,则下列命题中正确的有( )A、若 , 则存在实数使得 B、若 , 则 C、若 , 则在方向上的投影向量为 D、若存在实数使得 , 则11. 如图所示,设单位圆与轴的正半轴相交于点 , 以轴非负半轴为始边作锐角 , , , 它们的终边分别与单位圆相交于点 , , , 则下列说法正确的是( )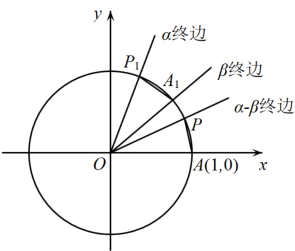 A、的长度为 B、扇形的面积为 C、当与重合时, D、当时,四边形面积的最大值为12. 已知正方体 , 棱长为分别是的中点,连接 , 记所在的平面为 , 则( )A、与正方体的棱有6个交点 B、 C、截正方体所得的截面面积为 D、与所成角的正弦值为
A、的长度为 B、扇形的面积为 C、当与重合时, D、当时,四边形面积的最大值为12. 已知正方体 , 棱长为分别是的中点,连接 , 记所在的平面为 , 则( )A、与正方体的棱有6个交点 B、 C、截正方体所得的截面面积为 D、与所成角的正弦值为三、填空题
-
13. 曲线的一个对称中心为(答案不唯一).14. 的展开式的常数项是 .15. 过圆上一点作圆的切线,切点为 , 则的最小值为.16. 定义在上的可导函数满足 , 且在上有成立.若实数满足 , 则的取值范围是 .
四、解答题
-
17. 已知 , , 分别为三个内角 , , 的对边,.(1)、求;(2)、若 , 的面积为 , 求 , .18. 全国中学生生物学竞赛隆重举行.为做好考试的评价工作,将本次成绩转化为百分制,现从中随机抽取了50名学生的成绩,经统计,这批学生的成绩全部介于40至100之间,将数据按照[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分成6组,制成了如图所示的频率分布直方图.
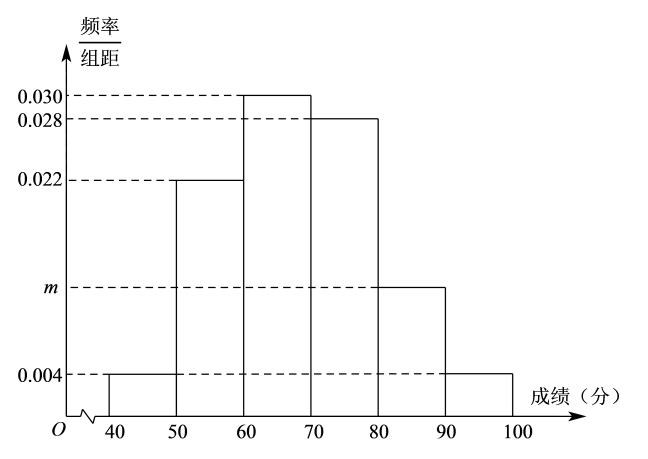 (1)、求频率分布直方图中的值,并估计这50名学生成绩的中位数;(2)、在这50名学生中用分层抽样的方法从成绩在[70,80),[80,90),[90,100]的三组中抽取了11人,再从这11人中随机抽取3人,记为3人中成绩在[80,90)的人数,求的分布列和数学期望;19. 已知等比数列的前项和为 , , 且满足.(1)、求的通项公式;(2)、若 , 求的前项和.
(1)、求频率分布直方图中的值,并估计这50名学生成绩的中位数;(2)、在这50名学生中用分层抽样的方法从成绩在[70,80),[80,90),[90,100]的三组中抽取了11人,再从这11人中随机抽取3人,记为3人中成绩在[80,90)的人数,求的分布列和数学期望;19. 已知等比数列的前项和为 , , 且满足.(1)、求的通项公式;(2)、若 , 求的前项和.
